高等教育出版常微分答案.pdf 36页

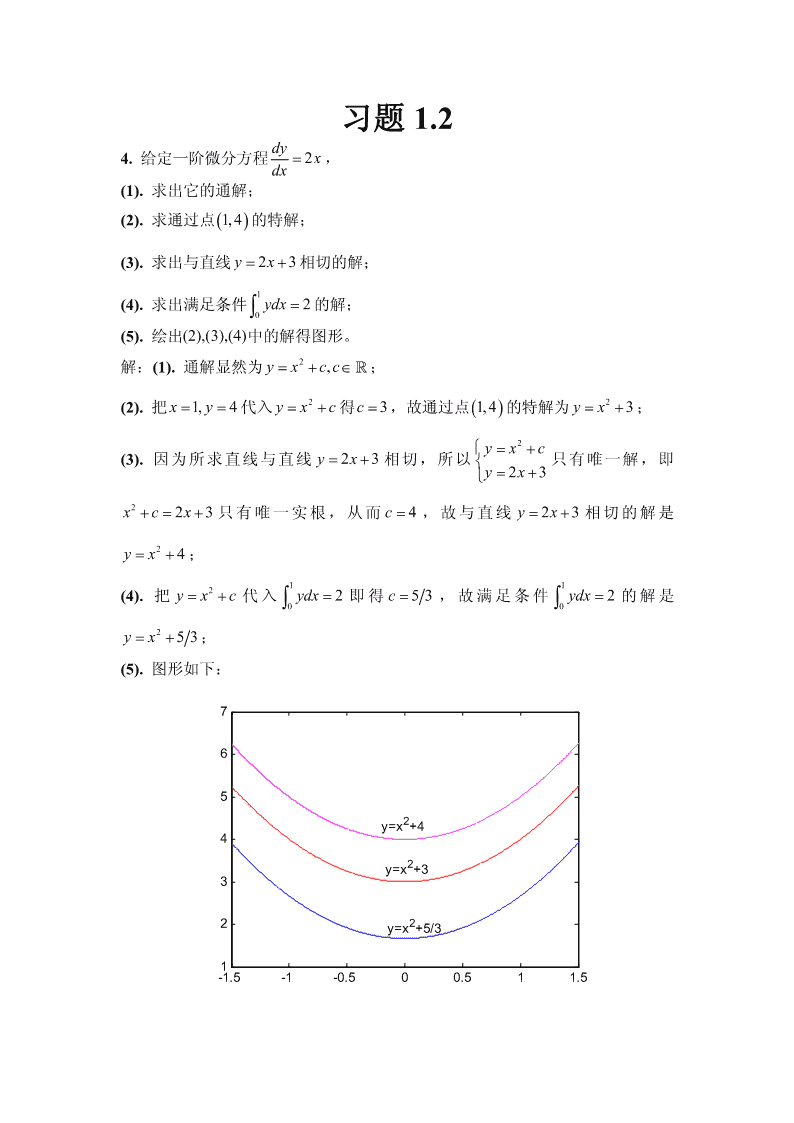
'习题1.2dy4.给定一阶微分方程=2x，dx(1).求出它的通解；(2).求通过点()1,4的特解；(3).求出与直线y=+23x相切的解；1(4).求出满足条件∫ydx=2的解；0(5).绘出(2),(3),(4)中的解得图形。2解：(1).通解显然为yxcc=+∈,；22(2).把xy==1,4代入y=+xc得c=3，故通过点(1,4)的特解为yx=+3；2⎧yxc=+(3).因为所求直线与直线y=23x+相切，所以⎨只有唯一解，即⎩yx=23+2x+=+cx23只有唯一实根，从而c=4，故与直线y=23x+相切的解是2yx=+4；112(4).把y=+xc代入∫ydx=2即得c=53，故满足条件∫ydx=2的解是002yx=+53；(5).图形如下：7652y=x+442y=x+3322y=x+5/31-1.5-1-0.500.511.5 5.求下列两个微分方程的公共解：24242y′′=+−yxx2,2yxxxyy=++−−24242解：由y+−=++−−22xxxxxyy可得22()yxx−(2210++=y)2222所以y=x或yx=−−12，y=x代入原微分方程满足，而yx=−−12代入原微分方程不满足，故所求公共解是代入原微分方程不满足。26.求微分方程yx′′+yy−=0的直线积分曲线。解：设所求直线积分曲线是y=+kxb，则将其代入原微分方程可得⎧kb−=02kx+−−=⇒kkxb00⎨⇒==kb或kb==12⎩kk−=0所以所求直线积分曲线是y=0或y=x+1。8.试建立分别具有下列性质的曲线所满足的微分方程：(2).曲线上任一点的切线介于两坐标轴之间的部分等于定长l；(5).曲线上任一点的切线的纵截距等于切点横坐标的平方。y解：因为过点()x,y的切线的横截距和纵截距分别为x−和y−xy′，故y′2⎛⎞y22(2).⎜⎟x−+−=()yxy′l；⎝⎠y′2(5).y−=xy′x。习题2.11.求下列方程的解：2(2).ydxx++()10dy=，并求满足初值条件x=0,y=1的特解；解：当y≠0，分离变量，得11dy=−dx2yx+1两边同时积分，得 11=+lnxcy1+⇒=yxln+1+c2又y=0也是原方程的解，故ydxx+(+=10)dy的通解是⎧1⎪,c∈y=⎨lnxc++1⎪⎩01由初值条件x==0,y1可得c=1，故所求特解是y=。ln1+x+1(4).(1++xydx)(1−=yxdy)0解：当y≠0，分离变量，得11−y+xdy=dxyx两边同时积分，得lnx++xyyln−=⇒cxlnyx+−=yc又y=0也是原方程的解，故所求通解是y=0和lnxy+x−=∈ycc,(5).()()0y++−=xdyxydx解：原方程可化为y−1dyy−xx==dxy+xy+1xy令u=，则xduu−11u+1u+=⇒x−du=dx2dxu++11ux两边同时积分，得12arctanuux+ln(1+=)−+lnc2y将u=代入，得所求通解是x y122arctan+ln(xyc+=∈),cx2dy22(6).xyxy−+−=0dx解：原方程可化为222dyyxy−−y⎛⎞y==−1−⎜⎟dxxx⎝⎠xy令u=，则x2du2du1−uux+=u−−⇒=1u−(1)dxdxx2当10−≠u，分离变量，得dudx=−1−u2x两边同时积分，得arctanux=−+lnc222又10−=u，即u=1也是(1)的解，故(1)的通解是u=1和arctanux=−ln+c。y将u=代入，得原方程的通解是x22yy=x和arctan+lnxcc=∈,x(7).tanydx−=cotxdy0解：当tany≠0，分离变量，得cotydy=tanxdx两边同时积分，得lnsinyx=−lncos+⇒csincosyx=c,c=±ec1≠01又tany=0，即siny=0也是原方程的解，而该解可在sincosyxc=中令c=0得到，故所求通解是sincosyxc=,c∈ 2yx+3dye(8).+=0dxy解：分离变量，得3x−y2eyedy=−dx两边同时积分，得所求通解是3x1−y2e3xy−2−=ec−+即23eec−==∈,6cc1123(9).(lnxxyd−−ln)yydx=0解：原方程可化为dyyy−1⎛⎞y==−ln⎜⎟dxx(lnx−ln)yx⎝⎠xy令u=，则xduuduuu(ln+1)ux+=−⇒=−(2)dxlnudxxlnu当uu()ln+≠10，分离变量，得lnududxlnud(lnu)dx=−⇒=−uu()ln++1xlnu1x两边同时积分，得u−cln=−+⇒+lnxclnu1==cxuce,±≠10(3)1lnu+1由原方程可得y≠0，从而u≠0。又uu(ln+1)=0，即lnu=−1也是(2)的解，而y该解可在(3)中令c=0得到，故(2)的通解是lnuc+1=∈xu,c。将u=代入，得x原方程的通解是yln+1=∈cyc,xdyx−y(10).=edx解：分离变量，得yxedyedx= 两边同时积分，得所求通解是yxeec=+∈,c2.作适当的变量变换求解下列方程：dy2(1).=+()xydx解：令uxy=+，则原方程化为dudy2du=+=+⇒11ud=x2dxdx1+u两边同时积分，得arctanuxcc=+∈,将uxy=+代入，得原方程的通解是arctan()xyxcc+=+∈,即yx=tan(+−∈c)x,cdy21x−−y(3).=dxx−+21y解：因为⎧21xy−−=011⎨⇒=−xy,=⎩xy−+=2103311令XxYy=+,=−，则原方程化为33dY2X−Y=dXX−2YY再令u=，得Xdu2−u(12−udu)dXuX+=⇒=2dX12−u21()−+uuX两边同时积分，得ln()uu22−+=−12lnXcXuu+⇒(2−+=1)cce,=>c10122Y11将uX==,,xY+=y−代入，得原方程的通解是X3322xyx+−+−==−>yxyc,1cc3−132 3dy2x+3xy+x(7).=23dx3xy+2y−y解：原方程可化为22dy231x+y+=222dx321x+y−22令XxYy=−=+1,1，则原方程化为dY23X+Y=dX32X+YY再令u=，得X2du23+udu21(−u)uX+=⇒=dX32++udXX()32u用分离变量法求解，得45cu()()+=11X−uY22将uX==,1xY−,1=y+代入，得原方程的通解是X52222cxy()+=−−∈(xy2,)c习题2.21.求下列方程的解：dy12−x(5).+−y10=；2dxx解：原方程可化为：dy21x−=y+1(4)2dxxdy12−x21x对应的齐次方程为=−y，用变量分离法求得其解为y=cxe。令(4)的2dxx21x解为ycxxe=()，则将其代入(4)可得dcx()21xx−1xec=1⇒=+()xecdx所以原方程的通解为−12xx1221xyecx=+()exc=+xec,∈ dyy(8).=；3dxx+y解：当y≠0时，原方程可化为：3dxx+yx2==+y(5)dyyydxx这是未知函数为x的非齐次线性方程，对应的齐次方程为=，用变量分离法dyy求得其解为x=cy。令(5)的解为x=cyy()，则将其代入(5)可得dcy()221yycy=⇒=+()ycdy2所以(5)的通解为⎛⎞12xyycc=⎜⎟+∈,⎝⎠2又y=0也是原方程的解，故原方程的通解为⎛⎞12y=0和xyycc=⎜⎟+∈,⎝⎠2(12).(ln2)yxy−=dxxdy；解：原方程可化为：dylnx22=yy−(6)dxxx2这是n=2的Bernoulli方程。当y≠0时，(6)两边同时除以y，得−−21dy2lnxyy=−+dxxx−1令zy=，则dz−2dy2lnx=-yz=−(7)dxdxxxdz222其对应的齐次方程=z的解为zc=x，令(7)的解为zcxx=()，则将其代入(7)dxx可得dcx()22lnx−−2xc=−⇒()x=()c+2lxnx+x4dxx 所以(7)的通解为2zc=++∈(x2lnx14,)c−12将zy=代入，得ycx()++2lnx1=4。又y=0也是原方程的解，故原方程的通解为2y=0和ycx(+2lnx+=∈1)4,c2(13).2(xydy=−2)yxdx；解：原方程可化为：2dy21y−xy==−(8)dx22xyxy这是n=−1的Bernoulli方程，(8)两边同时乘以y，得2dyy1y=−dxx22令zy=，则dzdy2z=2y=−1(9)dxdxxdz2z22其对应的齐次方程=的解为zc=x，令(9)的解为zcxx=()，则将其代入(9)dxx可得dcx()21xc=−⇒1()x=+cdxx所以(9)的通解为⎛⎞122zcxc=+⎜⎟=+∈xx,c⎝⎠x2将zy=代入，得原方程的通解为22yc=xx+∈,cxx(16).ye=+∫ytd()t；0解：原方程两边同时对x求导可得dyx=+eyx()dx 在原方程中，当x=0时，y=1。故原方程等价于Cauchy问题⎧dyx⎪=ey+⎨dx(10)⎪⎩y()01=dyxx由常数变易法易得=+ey的通解为yexcc=(+∈),，再由y()01=可得dxxc=1，故Cauchy问题(10)的解为yex=(+1)，这也是原方程的解。习题2.31.验证下列方程是恰当方程，并求出方程的解：2(2).0(y−3x)dx−4(y−x)dy=；2解：因为M=−yxN3,=−−(4yx)，所以∂MN∂=1,=1∂∂yx故原方程是恰当方程。∂∂uu∂u令函数u满足==M,N，则由=M可得∂∂xy∂x23uyx=−∫()3dxyx+=−+ϕϕ()yxy()∂u再由=N可得∂ydyϕ()2x+=−(4yx−)⇒=ϕ()y−2ydy32所以ux=−−yxy2，故原方程的通解是32xy−x−=∈2,ycc2322(2).03(2xy+2x)dx+2(3xy+y)dy=；2322解：因为M=+=+2(3xy2),xN3(2xyy)，所以∂∂MN==12xyx,12y∂∂yx 故原方程是恰当方程。∂∂uu∂u令函数u满足==M,N，则由=M可得∂∂xy∂x23224ux=++∫23()y2xdxϕϕ(y)=3xy+xy+()∂u再由=N可得∂ydyϕ()222363xyx+=+()2yy⇒=ϕ()yydy2243所以ux=+3yxy+，故原方程的通解是22433,xyx++=∈ycc2.求下列方程的解：22(4).ydxxdy−=+()xydx；22解：原方程两边同时除以x+y，得ydx−xdy⎛⎞x=dx⇒=d⎜⎟arctandx22xy+⎝⎠y所以原方程的通解是xarctan=xcc+∈,y(6).()y−1−xydx+xdy=0；∂MN∂解：因为Myx=−−()1,,1,1yNx==−x=，所以原方程不是恰当的。由∂∂yx∂∂MN−∂∂yx∫()−1dx−x=−⇒1ee=N−x可得积分因子μ=e，原方程两边同时乘以μ，得−−xx−−xxyedxedx−−+=xyedxxedy0即 −−−xxxydxe()+de+=xedy0所以−−xxxye+e=c故原方程的通解是xxy+=∈cec,(8).()x+2ydx+xdy=0；∂∂MN解：因为MxyNx=+2,=,=2,=1，所以原方程不是恰当的。由∂∂yx∂∂MN−1∂∂yx1∫dx=⇒=exxNx可得积分因子μ=x，原方程两边同时乘以μ，得22xdx+20xydxxdy+=即1322dx+ydx+=xdy03所以132xxycc+=∈,3此即为原方程的通解。5.试证齐次微分方程M()x,ydx+N(x,y)dy=0当xM+yN≠0时有积分因子1μ=。xMy+N证明：齐次微分方程M()x,ydx+N(x,y)dy=0两边同时乘以μ得μμMxydxNxydy(),,+()=0所以 ∂∂M⎛⎞MN∂()xM+−yNMx⎜⎟++Ny∂()μM∂⎛⎞M∂y⎝⎠∂∂yy==⎜⎟2∂∂+yyxM⎝⎠yN()xM+yN∂∂MNyN⋅−−⋅MNyM∂∂yy=2()xM+yN∂∂NM⎛⎞∂N()xM+−++yNNM⎜⎟xy∂()μN∂⎛⎞N∂x⎝⎠∂∂xx==⎜⎟2∂∂+xx⎝⎠xMyN()xM+yN∂∂NMxM⋅−−⋅MNxN∂∂xx=2()xM+yNdyM()xy,原方程可化为=−。因为原方程是齐次方程，故可设dxNxy(),dyMxy(,)⎛⎞y=−g⎜⎟dxNxy(),⎝⎠xy令u=，则x∂∂gdgduydggdgdud1g==,==2∂∂xdudxxduydudyxdu又因为∂gM∂∂⎛⎞Mxy(,)1⎛⎞∂N=−⎜⎟=−⎜⎟NM⋅−⋅∂x∂∂xNx⎝⎠⎜⎟(),yN2⎝⎠x∂x∂gM∂∂⎛⎞Mxy(,)1⎛⎞∂N=−⎜⎟=−⎜⎟NM⋅−⋅∂y∂∂yNx⎜⎟(),yN2y∂y⎝⎠⎝⎠所以ydg1⎛⎞∂∂∂∂MNMNy2dg=−⎜⎟NMNMN⋅−⋅⇒⋅−⋅=−⋅222xduN⎝⎠∂∂∂∂xxxxxdu11dg⎛⎞∂∂∂∂MNMN21dg=−⎜⎟NMNMN⋅−⋅⇒⋅−⋅=−⋅2xduN⎝⎠∂∂∂∂yyyyxdu从而 ∂∂MN∂NM∂yN⋅−−⋅MNyMxM⋅−−⋅MNxN∂∂()μμMN()∂∂yy∂x∂x−=−22∂∂yx()xM++yN()xMyN⎛⎞∂∂MN⎛⎞∂∂NMyN⎜⎟⋅−⋅−⋅−⋅MxM⎜⎟N⎝⎠∂∂yy⎝⎠∂∂xx=2()xM+yN⎛⎞221dg⎛⎞ydgyN⎜⎟−⋅−−⋅xN⎜⎟2⎝⎠xdu⎝⎠xdu=2()xM+yN=01故μ=是齐次微分方程M(x,y)dx+N(x,y)dy=0当xM+≠yN0时的积xMy+N分因子。习题2.41.求解下列方程：3(1).yx′=1+y′；解：当y′≠0时，原方程可化为11x=+32y′y′11令p=y′，则x=+，两边对y求导，得32pp13⎛⎞2dp=−⎜⎟+43p⎝⎠ppdy即⎛⎞3232dy=−⎜⎟+dp⇒=y++c322⎝⎠pp2pp又y′=0时，原方程恒不成立，所以原方程的参数形式的通解是⎧11x=+⎪32⎪pp⎨,pc为参数,∈⎪yc=++322⎪⎩2pp 2y′(3).y=y′e；2p解：令p=y′，则y=pe，两边对x求导，得pp2dppp=+()2epedx所以代入原方程py=⇒=⎯⎯⎯⎯00′→=y0或ppdp12=+()pexp⇒=+()1e+cdx所以原方程的通解是p⎧⎪xp=+(1)e+cy=0和⎨,pc为参数,∈2p⎪⎩yye=习题2.51.求解下列方程：dy−y(3).=−4sexin1；dxy解：原方程两边同时乘以e，得yyydydeyex=−4sine⇒=−4sinxedxdxy令ue=，则du=4sinx−udxx−x用常数变易法易得其解为ux=−+2sin(cosx)ece，故原方程的通解为yx−xex=−+∈2sin()cosxece,cdyx−+y1(11).=；2dxx++y3解：原方程可化为2()x−+y13dx−++(xy)dy=02∂−+()xy1∂−−−()xy3由=−1,=−1可得，这是一个恰当方程，即∂∂yx 22113xdx−+−−−=⇒−+−−=ydxdxxdyydy30dydxdxydxdy30dy23所以原方程通解为1123xx−+−−=∈yxyyc3,c232⎛⎞dy⎛⎞dy(19).xyx⎜⎟−+24⎜⎟=0；⎝⎠dx⎝⎠dx解：令p=y′，则由原方程可得p≠0，故原方程可化为2xpxxx+42yp==+(11)22pp两边对x求导，得pxdp22xdp⎛⎞p2⎛⎞12dppx=++−⇒−=⎜⎟⎜⎟−2222dxppdx⎝⎠2p⎝⎠2pdx所以p2代入(11)−=⇒=±⎯02p⎯⎯⎯→=±yx22p或xdp代入(11)1221,=⇒pc=x⎯⎯⎯⎯→=ycx+c≠0pdx2c又y′=0时，原方程恒不成立，所以原方程的参数形式的通解是122y=±2x和yc=xc+≠,02cdyyxy(29).+=e；dxxdudy解：令ux=y，则=+yx，故dxdxduu⎛⎞uuu−−uu12=+x⎜⎟ex−=⇒eedu=⇒−=xdxex+c2dxx⎝⎠x2所以原方程通解为12−xyxecc+=∈,2 习题3.1dy21.求方程=+xy通过点(0,0)的第三次近似解。dx2解：f()xy,=+xy，令ϕ()xy==0，则00xx12ϕϕ10()x=+yf∫∫()xx,0()dxx=dxx=x0022xx⎡⎤⎛⎞11251ϕϕ20()x=+y∫∫fx(),1()xdx=⎢⎥x+⎜⎟xdx=+xxx00⎢⎥⎣⎦⎝⎠2220xϕϕ30()xy=+∫fxxd(),2()xx02x⎡⎤⎛⎞1125111125811=++∫⎢⎥x⎜⎟xxdxxxx=+++x0⎢⎥⎣⎦⎝⎠2202201604400为所求的第三次近似解。3.求初值问题⎧dy22⎪=−xyRx,:11+≤≤,y1,⎨dx(12)⎪⎩y()−=10的解的存在区间，并求第二次近似解，给出在解的存在空间的误差估计。22解：因为f()xy,=−xy，ab==1，Mf=max(x,y)=4，所以()xyR,∈⎛⎞b1153ha==min⎜⎟,，从而解得存在区间为x+1≤，即−≤≤−x。⎝⎠M444422又因为f()xy,=−xy在R上连续，且由∂f∂=yyL22≤=可得f()xy,在53R上关于y满足Lipschitz条件，所以Cauchy问题(12)在−≤≤−x有唯一解44y=ϕ()x。令ϕ()xy==0，则00xx123ϕϕ10()xy=+∫∫fxxd(),10()xx=dxx=()+x0−132347xx⎡⎤23⎛⎞111xxxxϕϕ20()xy=+∫∫fxxd(),11()x=⎢⎥x−⎜⎟()x+dx=−+−−x0−1⎢⎥⎣⎦⎝⎠342931863 3M()Lh1误差为：ϕϕ()()xx−≤=2L()21!24+10.给定积分方程bϕ()x=+fx()λ∫Kx()(),ξϕξξd(*)a其中f()x是[ab,]上的已知连续函数，Kx(,ξ)是axb≤≤，ab≤ξ≤上的已知连续函数。证明当λ足够小时(λ是常数)，(*)在[ab,]上存在唯一的连续解。证明：分四个步骤来证明。㈠.构造逐步逼近函数序列ϕ0(x)=fx()bϕλnn+1()xfx=+()∫Kx()(),ξϕξdnξ,=0,1,2,"a由f()x是[ab,]上的连续函数可得ϕ(x)在[ab,]上连续，故再由Kx(),ξ是0axb≤≤，ab≤≤ξ上的连续函数可得ϕ(x)在[ab,]上连续，由数学归纳法易证1ϕn()x在[ab,]上连续。㈡.证明函数列{ϕ()x}在[ab,]上一致收敛。n考虑级数∞ϕϕ01()x+−∑()kk()xxxϕ−(),,∈[]ab(13)k=1由nϕϕ01()x+−=∑()kk()xxxϕϕ−()n()k=1知，{ϕ()x}的一致收敛性与级数(13)的一致收敛性等价。n令M=maxfx()，Lb=−λ(aK)max(x,ξ)。由(13)有axb≤≤axb≤≤,ab≤≤ξ bϕϕλξξ10()xxK−=()∫()()x,fdξab≤λξ∫Kx(),f()ξdξab≤=λξξmaxKx(),maxf()∫dξMLaxb≤≤,a≤≤ξbaab≤≤ξ所以bϕ21()x−=ϕλξ()xK∫()()()x,()ϕ10ξ−ϕξdξab≤−λ∫Kx(),ξϕξϕξξ10()()dab2≤≤MLλξ∫Kx(),dξMLa假设对正整数n，有不等式nϕϕnn()x−≤−1(xM)L,,xa∈[b](14)则bϕϕλξnn+−11()xxK−=()∫()()()x,()ϕnnξ−ϕξdξab≤−λξ∫Kx(),ϕnn()ξϕ−1()ξdξabnn−1≤≤MLKλξ∫()x,,dξMLx∈[]a,ba所以(14)对任意正整数n都成立。∞n因为∑ML为正项级数，且当λ足够小时，n=1Lb=−λξ(aK)max(x,)<1(15)axb≤≤,ab≤≤ξ∞∞n故∑ML收敛，从而由Weierstrass判别法，级数∑()ϕϕkk()x−−1()x一致收敛，n=1k=1故级数(13)一致收敛，所以函数列{ϕ(x)}在[ab,]上一致收敛。n㈢.证明limϕϕ()x=()x是积分方程(*)在[ab,]上的连续解。nn→∞因为由㈠和㈡可得ϕ()x在[ab,]上连续，{ϕ(x)}在[ab,]上一致收敛，故nnϕ()x在[ab,]上连续，且函数列{Kx(,ξϕ)n(x)}在[ab,]上一致收敛，所以对 bϕnn+1()x=+fx()λ∫Kx()(),ξϕξξda两边取极限可得blimϕnn+1()x=+fx()λξlim∫Kx()(),ϕξdξnn→∞→∞ab=+f()xKλ∫()x,lξϕimn()ξξdan→∞从而bϕ()x=+fx()λ∫Kx(),ξϕξξ()da所以ϕ()x是积分方程(*)在[ab,]上的连续解。㈣.证明ϕ()x是积分方程(*)在[ab,]上的唯一解。设ψ()x是积分方程(*)在[ab,]上的另一连续解，则bψ()x=+fx()λ∫Kx(),ξψξξ()da令gx()=−ψϕ()x()x，则bgx()=−λξ∫Kx(),()ψ()ξϕ()ξdξab≤−λξ∫Kx(),ψ()ξϕ()ξdξab≤−maxψ()xϕλ()xK∫()xd,ξξaxb≤≤a≤Lgmax()xaxb≤≤对∀∈x[ab,]都成立，上式两边对x取最大值可得maxgxL()≤maxgx()axb≤≤axb≤≤如果maxgx()≠0，则由上式有axb≤≤L≥1这与(15)矛盾，故maxgx()=0，即gx()≡0，所以ψϕ(x)≡(x)，从而ϕ()x是积axb≤≤分方程(*)在[ab,]上的唯一解。证毕。习题3.2 1.求⎧dy2⎪=+1y⎧−∞<<∞x⎫⎨⎨dx,,()xyG∈=⎬(16)⎪y()00=⎩⎭−∞<<∞y⎩的解的存在区间及延拓解的饱和区间。⎧⎪x≤⎫a⎪2解：对任意充分大的ab,，令R=⎨⎬，则f(xy,1)=+y在R上连续且关于y⎩⎭⎪y≤b⎪⎧dy2⎪=1+y满足Lipschitz条件，故(16)存在唯一解。由⎨dx可得y=tanx，解的存在⎪⎩y()00=⎛⎞b区间为x≤h，ha=min⎜⎟,。由于ab,充分大，故存在充分小的δ>0，使2⎝⎠1+b得(16)的解的存在区间为x<δ。2由于f()xy,1=+y在G上连续和关于y满足局部Lipschitz条件，故解y=tanx，x<δ可延拓。+−又当x→−()π2时，tanx→−∞；x→()π2时，tanx→+∞，故由推论，延拓解的饱和区间为−<()π22x<π。习题4.13.已知齐次线性微分方程的基本解组x,x，求下列方程对应的非齐次线性微分12方程的通解：t1t(2)x′′+−=xx′tx−==1,t,xe1211−−tt解：令所求通解为tx(tcttcte)=+12()()则t⎧⎪⎪cttcte12′′()+=()0⎧⎧ct11′()=−1⎪ct()=−+tγ1⎨⎨⇒⇒⎨⎪cttcte′′′+=t′t−1⎪⎪⎩⎩ctte′()=−−ttct()=−+(te1)+γ⎩12()()()222所以，所求通解为t2x()ttett=γγ12+−−−1 22(5)txtxx′′−+=+′63t4,txtxtt==,ln1222xx′6解：txtxx′′−+=+⇔−+=+′63t4tx′′34令所求通解为2tttx(tcttcttt)=+12()()ln则⎧⎛⎞6⎧cttcttt12′′()+=()ln0⎪ct1′()=−lnt⎜⎟+34⎪⎪⎝⎠t⎨⎨6⇒⎪⎪cttcttt12′′′()+=()(ln)′+346⎩t⎪⎩ct2′()=+34t2⎪⎧ct11()=341lnt(−−+t)3lntγ⇒⎨⎪⎩ct22()=++34t6lntγ所以，所求通解为22x()ttt=+γγ12lntttt++343ln2dxt−t4.已知方程−x=0有基本解组为e,e，试求此方程适合初值条件2dtxx(01,00)=′()=及xx(00,01)=′()=的基本解组（称为标准基本解组，即有W(01)=），并由此求出方程的适合初值条件x(0,0)=xxx00′()=′的解。22t−tdxdx解：因为e,e是方程−=x0的基本解组，故−x=0的通解为22dtdttt−xtcece()=12+∈,,cc12由xx()01==,00′()可得，⎧cc+=11112tt−⎨⇒==⇒cc12xt()=()ee+=cht⎩cc−=02212由xx()00==,01′()可得， ⎧cc+=011112tt−⎨⇒=cc12,s=−⇒x()te=()−=eth⎩cc−=1222122dx又cht和sht线性无关，所以−x=0适合初值条件xx(01)(==,00′)及2dt2dxxx()00==,01′()的基本解组为cht，sht，从而−x=0的通解又可表示为2dtxtctct()=+121chsh,cc,2∈故由x()0,0==xx′()x′可得cxcx=,=′，于是适合初值条件001020x()0,0==xx00′′()x的解为x(txtxt)=+00ch′sh习题4.22.求解下列常系数线性微分方程：(4)(1)xxx−+=540′′42解：特征方程：λλ−+=540特征根：λ=2211，，，λλλ=−==−123422tt−−tt基本解组：eeee,,,所求通解：22tt−−ttxcecececec=+++,,∈=i1,2,3,41234i23(2)xa′′′−+−=33xa′′xa′x03223解：特征方程：λ−3aλ+3aλ−a=0特征根：λ=a1,2,3atat2at基本解组：etete,,所求通解：2atxcc=++()123tcteci,,i∈=1,2,3(5)(3)xx−=40′′′ 53解：特征方程：λ−4λ=0特征根：λ===022，，λλ−1,2,345222tt−基本解组：1,,,ttee,所求通解：222tt−xcctctcecec=++++,∈=,i1,2,3,4,512345i(4)xxx′′++=′02解：特征方程：λ+λ+1=0−±13i特征根：λ=1,2211−−tt33基本解组：et22cos,etsin22所求通解：11−−tt33xce=+∈22costcesintc,,i=1,212i222(5)sast′′−=+1（属于类型Ⅰ）2解：齐次方程：sas′′−=022特征方程：λ−a=0特征根：λ=aa,λ=−12at−at当a≠0，齐次方程通解：scecec=+,,∈=i1,2，此时0不是特征根，12i1故设特解为sA=+tB，将其代入原方程可得A=B=−，从而特解为2a1st=−()+1，所以所求通解：2aat−at1scece=+−+∈=122()t1,ci,1,2ia当a=0，0是二重特征根，故齐次方程通解：scctc=+∈=,,i1,2，设特12i211解为stA=+()tB，则将其代入原方程可得AB=,=，从而特解为622⎛⎞11stt=+⎜⎟，所以所求通解：⎝⎠62 2⎛⎞11sccttt=++⎜⎟+,,c∈=i1,212i⎝⎠62(6)x′′′−+−=+45223xxxt′′′（属于类型Ⅰ）解：齐次方程：xxxx′′′−+−=4520′′′32特征方程：λ−4λ+5λ−2=0特征根：λ=1,λ=21,23tt2齐次方程通解：xcc=+()tec+eci,,∈=1,2,3123i0不是特征根，故设特解为x=At+B，将其代入原方程可得AB=−1,=−4，从而特解为x=−−t4，所以所求通解：tt2xcc=+()12tec+−−∈=3etci4,i,1,2,3(4)2(7)xx−+=−23′′xt（属于类型Ⅰ）(4)解：齐次方程：xx−+=20′′x42特征方程：λλ−+210=特征根：λ=1,λ=−11,23,4tt−齐次方程通解：xcc=+()tecc++(teci),,∈=1,2,3,41234i方法一：常数变易法求解tttt−−设原方程通解为x=+++ctecttectectte()()()()，则1234tttt−−⎧ctectt1234′′′′()+++=()ectectt()()e0⎪⎧ct1′()="⎧ct1()="⎪cte′′′′()()tttt′′′′+++=ctte()()cte()()−−ctte()()0⎪⎪⎪1234⎪ct2′()="⎪ct2()="⎨⎨⇒⇒⎨⎪⎪c′′′′()tec()tttt′′+++=()t()tec′′()tec()−−′′()t()te′′0ct3′()="⎪ct3()="1234⎪⎪⎪⎪tttt′′′′′′−−′′′′′′2⎩ct4′()="⎩ct4()="⎩cte1234′′′′()()+++=ctte()()cte()()ctte()()t−3tttt−−所以将cti(),=1,2,3,4代入x=+++ctecttectectte()()()()中即得原方i1234程通解：tt−2x=+()ccte12++(ccte34)++∈=t1,ci,i1,2,3,4方法二：比较系数法求解 2由于0不是特征根，故设特解为x=At++BtC，将其代入原方程可得2ABC===1,0,1，从而特解为xt=+1，所以所求通解：tt−2x=+()ccte12++(ccte34)++∈=t1,ci,i1,2,3,4t(10)x′′′−=xe（属于类型Ⅱ）解：齐次方程：xx′′′−=03特征方程：λ−1=0−±13i特征根：λλ=,1=1,23211−−tt33齐次方程通解：xce=++22costcesintcect,∈,i=1,2,3123i22t1由于1是一重特征根，故设特解为x=Ate，将其代入原方程可得A=，从31t而特解为x=te，所以所求通解：311−−tt33tt1xce=++22costcesintcet+ec,∈,i=1,2,3123i2232t(12)x′′+6x′+5x=e（属于类型Ⅱ）解：齐次方程：xxx′′′++=6502特征方程：λ+6λ+5=0特征根：λ=−=1,λ−512−−tt5齐次方程通解：xcecec=+,,∈=i1,212i2t1由于2不是特征根，故设特解为x=Ae，将其代入原方程可得A=，从211t而特解为x=e，所以所求通解：21−−ttt51xcece=++ec,,∈=i1,212i21(14)x′′+x=sint−cos2t（属于类型Ⅲ的混合，注意sint和cos2t中t的系数不一样）解：齐次方程：xx′′+=02特征方程：λ+1=0 特征根：λ=±i12，齐次方程通解：xctctc=+∈cossin,,i=1,212i①对于x′′+=xtsin，由于α+iiβ=是一重特征根，故设其特解为1x10=+tA()costA1sint，则将其代入x′′+xt=sin可得AA01=−=,0，从而21x′′+=xtsin的特解为x=−ttcos；12②对于x′′+=xtcos2，由于α+iiβ=2不是特征根，故设其特解为1x=+Btcos2Btsin2，则将其代入x′′+xt=cos2可得BB=,0=，从而2010131x′′+=xtcos2的特解为x=cos2t。2311所以原方程特解为x=+=−xxttcos+cos2t，故所求通解：122311xctcttt=+−+cossincoscos2,tc∈,i=1,212i23tt2(15)xxxee′′−+=++44′1（属于类型Ⅰ和Ⅱ的混合）解：齐次方程：xxx′′′−+=4402特征方程：λλ−+=440特征根：λ=212，2t齐次方程通解：xcc=+()teci,,∈=1,212itt①对于x′′−+=44xxe′，由于1不是特征根，故设其特解为x=Ae，则将10ttt其代入x′′−+=44xxe′可得A=1，从而x′′−44xxe′+=的特解为x=e；012t22t②对于x′′−+=44xxe′，由于2是二重特征根，故设其特解为x=Bte，202t12t则将其代入x′′−44xxe′+=可得B=，从而x′′−44xxe′+=的特解为02122tx=te；22③对于x′′−+=441xx′，由于0不是特征根，故设其特解为x=C，则将其3011代入x′′−+=441xx′可得C=，从而x′′′−441xx+=的特解为x=。0344 tt1122所以，原方程特解为xxxxete=++=++，故所求通解：1232422tt112txcc=+()12teete+++∈=,,cii1,2241(20)xx′′+=−1（不属于类型Ⅰ、Ⅱ、Ⅲ的混合，用常数变易法求解）sint解：齐次方程：xx′′+=02特征方程：λ+1=0特征根：λ=±i12，齐次方程通解：xctctc=+∈cossin,,i=1,212i设原方程通解为x=+ct()costct()sint，则12⎧⎪⎪ct12′′()costct+=()sint0⎧ct′()=−1sint⎪⎧ctt()=+cost11⎨⎨1⇒⇒⎨⎪ct12′′()(costct)′′+=()(sint)1−⎩⎩⎪ct22′()=−costcott⎪ct()=−sintlnsint⎩sint所以所求通解：x=++ctcttttt12cossin(+cos)cos+−(sinlnsintt)sin=++ctctttttcossin1+−cossinlnsin,ci∈,=1,212i3.求下列方程的通解：2(1)txtxx′′+−=′0u解：做变换te=，则22dx11dxdx⎛⎞dxdx==,⎜⎟−222dttdudtt⎝⎠dudu所以原方程可化为22dxdxdxdxuu−−+−=⇒xx00−=⇒=xce+ce,c∈=,i1,22212idudududu由ut=ln可得所求通解：c2xct=+,,c∈=i1,21it习题4.31.求解下列方程： 23(2)xx′′−+=()()x′x′0dx′dydydxdy解：令x′=y，则x′′====y，故原方程可化为dtdtdxdtdxdy23⎛⎞dy2xy−+=⇒yy00yx⎜⎟−+=yy（自变量为t，未知函数为y）dx⎝⎠dx所以yxx=00⇒=⇒=′c或dy2dydxyx′1x−+=⇒yy0l=⇒=⇒=⇒+cxcxxnxtc=+2112dxy−−−yx11yx′c1所以，原方程通解为1x+=lnxtc+或x=c，ccc,,∈212c12(4)xx′′+−10()′=解：令x′=y，则原方程可化为2yy′+−=10（自变量为t，未知函数为y）所以2101−=⇒=yxx′±⇒=±+tc或dy−=dt⇒=arccosytcy+1111⇒=+cos()tc⇒x′=+cos()tc⇒x=sin()tcc++221−y所以，原方程通解为x=±+tc或x=sin(tcc++)，ccc,,∈12122.用幂级数解法求解下列方程：(1)xt′′++=xxx′0,()0=0,x′()0=1解：因为pxtqx()==,1()能展成x的幂级数，且收敛区间为(−∞+∞,)，所以原方程有形如∞nx=∑atnn=0 的特解，且此解在()−∞+∞,上收敛。由xx(00)=,01′()=可得aa==0,1，所以01∞∞∞nn−12n−x=+ta∑∑∑nntx,1′′=+natxn,′=()na−1ntnnn===222将其代入原方程可得∞∞∞nn−−21⎛⎞n∑∑nn()−+11atnnt⎜⎟+nat+t+=∑atn0nn==22⎝⎠n=2∞∞nn−2∑∑nn()−+++11atnn()nat2t=0nn==22∞∞nn26aa23+tnnat+++∑∑()21()nn+2+++()na1tt20=nn==22所以⎧20aa=⇒=022⎪⎨620aa+=⇒=−1333⎪⎩()nnana+21()()++nn++22+=10⇒=aann−+n()2从而k()−1aa==0,,k=1,2,3,"22kk+1357⋅⋅⋅⋅"()21k+故所求解为∞k21k+()−1txt=+∑k=1357⋅⋅⋅⋅"()21k+习题5.12.将下面的初值问题化为与之等价的一阶方程组的初值问题：(4)t(2)x+=xte，x()01=，x′(01)=−，x′′(02)=，x′′′(00)=解：令x=x，x=x′，x=x′′，x=x′′′，则x′=xx′=，x′=xx′′=，x′==xx′′′，1234122334(4)tx′==xx−+te，且xx()00==()1，xx(001)=′()=−，xx(00)(==′′)2，4123xx4()00==′′′()0，所以原问题等价于 ⎧⎡⎤xx′⎡⎤0100⎡⎤⎡0⎤11⎪⎢⎥⎢⎥⎢⎥⎢⎥xx′00100⎪⎢⎥22=+⎢⎥⎢⎥⎢⎥⎪⎨⎢⎥xx33′⎢⎥0001⎢⎥⎢0⎥⎪⎢⎥⎢⎥⎢⎥⎢t⎥⎣⎦xx′⎣⎦−1000⎣⎦⎣te⎦44⎪⎪⎩xxxx12()01==,01()−==,0234(),00()3.试用逐步逼近法求方程组⎡01⎤xx′=⎢⎥⎣−10⎦满足初值条件⎡0⎤x()0=⎢⎥⎣1⎦的第三次近似解。⎡⎤0解：令ϕ()t==x()0⎢⎥，则0⎣⎦1tt⎡01⎤⎡⎤0⎡010⎤⎡⎤⎡⎤tϕϕ10()t=+x()0∫∫⎢⎥()tdt=+⎢⎥⎢⎥⎢⎥dt=⎢⎥00⎣−−10⎦⎣⎦1⎣101⎦⎣⎦⎣⎦1tt⎡⎤01⎡0⎤⎡⎤01⎡tt⎤⎡⎤ϕϕ21()t=+x()0∫∫⎢⎥()tdt=+⎢⎥⎢⎥⎢⎥⎢⎥dt=200⎣⎦−−10⎣1⎦⎣⎦101⎣⎦⎣⎦1−t23tt⎡⎤01⎡0⎤⎡⎤01⎡⎤t⎡⎤tt−6ϕϕ32()t=+x()0∫∫⎢⎥()tdt=+⎢⎥⎢⎥⎢⎥2dt=⎢⎥200⎣⎦−−10⎣1⎦⎣⎦101⎣⎦−t2⎣⎦12−t为所求的第三次近似解。习题5.28.考虑方程组xA′=+xf()t，其中⎡21⎤⎡sint⎤A=⎢⎥，f()t=⎢⎥⎣02⎦⎣cost⎦(1)试验证22tt⎡ete⎤Φ()t=⎢⎥2t⎣0e⎦是xA′=x的基解矩阵；⎡1⎤(2)试求xA′=+xf()t的满足初值条件ϕ()0=⎢⎥的解ϕ(t)。⎣−1⎦ 解：(1)因为22tt′2t2t22tt⎡⎤ete⎡21e()+2te⎤⎡⎤⎡⎤21eteΦ′()tt==⎢⎥22tt⎢⎥⎢⎥=⎢⎥2t=AΦ()⎣⎦00ee⎣2⎦⎣⎦⎣⎦020e4t所以Φ()t是xA′=x的解矩阵，又因为detΦ(te)=≠0，故Φ(t)是xA′=x的基解矩阵。(2)由常数变易法，令xA′=+xf(t)的解为x=Φ(tt)C()，则x′′=+=+Φ()()ttttCΦ()CA′()Φ(ttt)Cf()()再由Φ′=AΦ可得Φ()()tttCf′=()，从而−2t−−12t⎡⎤1s−tt⎡⎤in⎡et(sin−tcost)⎤C′()tt==Φ()()fte⎢⎥⎢⎥=⎢−2t⎥⎣⎦01c⎣⎦ost⎣etcos⎦所以⎡⎤12−2t⎛⎞14⎢⎥ett⎜⎟2cos−−−costsintttsin55⎝⎠5⎡C1⎤C()t=+⎢⎥⎢⎥⎢⎥1−2t⎣C2⎦⎢⎥ett()sin−2cos⎣⎦5⎡1⎤故xA′=+xf()t得通解为x=Φ(tt)C()。由ϕ()0=⎢⎥可得，C=2725，1⎣−1⎦⎡1⎤C=−35，所以xA′=+xf()t的满足初值条件ϕ()0=⎢⎥的解2⎣−1⎦⎡⎤122t14()2715−−−tecostsint⎢⎥252525ϕ()t=⎢⎥⎢⎥1232tsintt−−cose⎢⎥⎣⎦555习题5.32.试证：如果ϕ(t)是xA′=x满足初值条件ϕ(t)=η的解，那么0ϕ(tt)=−⎡⎣expA(t0)⎤⎦η证明：因为expAt是xA′=x的基解矩阵，所以设ϕ(tt)=(expAC)。由ϕ()t=η可0−1得CA==()expttη⎡⎤exp()−Aη，故00⎣⎦ ϕ()(ttt=−expAA)⎡⎣exp(00)⎤⎡⎦⎣η=expA(t−t)⎤⎦η4.试求方程组xA′=x的一个基解矩阵，并计算expAt，其中A为：⎡⎤233−⎢⎥(3)A=−453⎢⎥⎢⎥⎣⎦442−解：由det()λEA−=0可得A的特征值为λ=−1，λ=−2，λ=2。123T由()λEAv0−=有v=[110]，111T由()λEAv0−=有v=[011]，222T由()λEAv0−=有v=[111]，333所以基本解组−tt2⎡ee0⎤Φ=()teeee⎡⎤vvvλλ12ttλ3t=⎢−−tttee22⎥⎣⎦123⎢⎥⎢0ee−22tt⎥⎣⎦⎡⎤101⎡011−⎤⎢⎥−1⎢⎥故Φ=()0111，从而Φ=()01−10，因此⎢⎥⎢⎥⎢⎥⎣⎦011⎢⎣111−⎥⎦22tt−−t2tt⎡ee−−eee⎤−−12⎢ttttttt2−−−222⎥expAtt=Φ()Φ()0=⎢eeeeeee−+−−⎥⎢ee22tt−−−−ee22tte2t⎥⎣⎦5.试求方程组xA′=x的基解矩阵，并求满足初值条件ϕ(0)=η的解ϕ()t：⎡⎤121⎡⎤1⎢⎥⎢⎥(3)A=−111，η=0⎢⎥⎢⎥⎢⎥⎣⎦201⎢⎥⎣⎦0解：方法一：（空间分解法）由det()λEA−=0可得A的特征值为λ=3，λ=−1，重数分别为n=1，n=2。1212n1T由()λEAu0−=有u=[212]，111n2TT由()λEAu0−=有u=−[120]，u=[304−]，2223 113令vu=α，vuu=β+γ，则由vv+=η可得α=++ηηη，11223121234816173115β=−+ηηη，γ=+−ηηη，所以xA′=x满足初值条件1231238163281632ϕ()0=η的解为3tt−ϕ()te=++−Ev12e⎡⎤⎣⎦Et(A2E)v⎡⎤113⎡113−−+−⎛⎞1⎤ηηη123++⎢ηηηηη12323t⎜⎟⎥⎢⎥248248⎝⎠2⎢⎥⎢⎥3tt⎢⎥113−⎢173⎛⎞11⎥=+eet⎢⎥ηηη123++⎢−ηηη123+−+⎜⎟⎝⎠−ηη23+⎥4816481624⎢⎥⎢⎥⎢⎥113⎢115⎛⎞1⎥ηηη++−−++−+ηηηηη⎢⎥⎣⎦248123⎣⎢248123t⎜⎟⎝⎠232⎥⎦⎡⎤13tt−⎢⎥()ee+2⎢⎥T⎢⎥13tt−当η=[100]时，ϕ1()te=−()e；⎢⎥4⎢⎥⎢⎥13tt−−()ee⎢⎥⎣⎦2⎡⎤113tt⎛⎞−⎢⎥ete+−⎜⎟44⎝⎠⎢⎥T⎢⎥173tt⎛⎞1−当η=[010]时，ϕ()te=+⎢⎥⎜⎟−te；2⎢⎥88⎝⎠2⎢⎥11⎛⎞3tt−⎢⎥ete−+⎜⎟⎣⎦44⎝⎠⎡⎤333tt⎛⎞1−⎢⎥et−+⎜⎟e88⎝⎠2⎢⎥T⎢⎥313tt⎛⎞3−当η=[001]时，ϕ()tete=+⎢⎥⎜⎟−，3⎢⎥16⎝⎠416⎢⎥313tt⎛⎞5−⎢⎥ete++⎜⎟⎣⎦82⎝⎠8所以⎡1133tt−−t⎛⎞1t33t⎛⎞31−t⎤⎢()ee++ete⎜⎟−e−⎜⎟+te⎥24⎝⎠48⎝⎠82⎢⎥⎢1133tt−−−t⎛⎞71t33t⎛⎞13t⎥expAtttte==⎡⎤⎣⎦ϕϕϕ123()()()⎢()−ee+⎜⎟−teete+⎜⎟−⎥⎢48⎝⎠8216⎝⎠416⎥⎢1133tt−−t⎛⎞1t33t⎛⎞15−t⎥⎢()ee−−ete⎜⎟+e+⎜⎟te+⎥⎣24⎝⎠48⎝⎠28⎦ 方法二：（Jordan标准型法）由det()λEA−=0可得A的特征值为λ=3，λ=−1（二重），所以123t⎡⎤300⎡e00⎤⎢⎥⎢−−tt⎥JJ=−⇒=011expte0te⎢⎥⎢⎥⎢⎥001−⎢00e−t⎥⎣⎦⎣⎦T由()λEAv0−=有v=[212]，111T由()λEAv0−=有v=−[212]，222T由()λEAvv−=有v=−−[112]，2323所以⎡221−−⎤⎢⎥Tvvv==[]123⎢111−⎥⎢⎣222⎥⎦⎡⎤1⎢⎥4⎡1⎤⎢⎥⎢⎥⎢⎥1故xA′=x得通解为xTJ()tt=(exp)C，由ϕ()00==η可得C=−，故⎢⎥⎢⎥4⎢⎣0⎥⎦⎢⎥0⎢⎥⎢⎥⎣⎦⎡13tt−⎤⎢()ee+⎥2⎢⎥xA′=x满足初值条件ϕ()0=η的解为()⎢13tt−⎥ϕte=−()e。⎢4⎥⎢⎥⎢13tt−−⎥()ee⎢⎣2⎥⎦另外，⎡⎤1133tt−−t⎛⎞1t33t⎛⎞31−t⎢⎥()ee++ete⎜⎟−e−⎜⎟+te24⎝⎠48⎝⎠82⎢⎥−−13⎢⎥11tt3t⎛⎞71−t33t⎛⎞13−texpATJTtte==()exp⎢⎥()−eet+⎜⎟−+ee⎜⎟t−e⎢⎥48⎝⎠8216⎝⎠416⎢⎥1133tt−−t⎛⎞1t33t⎛⎞15−t⎢⎥()ee−−ete⎜⎟+e+⎜⎟te+⎣⎦24⎝⎠48⎝⎠28方法三：（递推法）由det()λEA−=0可得A的特征值为λ=3，λ=−1（二重）。12 3t由rr′==λ,01r()有re=，111113tt−由rrrr′=+λ,00()=有ree=−()4，2122223tt−由rrrr′=+λ,00()=有rete=−+()(41)16，323333⎡⎤−221⎡042−⎤⎢⎥⎢⎥又P=E，P=−=AEλ141−，PP=()AE−=λ021−，所以011⎢⎥212⎢⎥⎣⎦⎢⎥202−⎢⎣042−⎥⎦⎡⎤1133tt−−t⎛⎞1t33t⎛⎞31−t⎢⎥()ee++ete⎜⎟−e−⎜⎟+te24⎝⎠48⎝⎠82⎢⎥⎢⎥1133tt−−−t⎛⎞71t33t⎛⎞13texpAtrPrPrP=++=102132⎢⎥()ee−e+−⎜⎟tee+−⎜⎟te⎢⎥48⎝⎠8216⎝⎠416⎢⎥1133tt−−t⎛⎞1t33t⎛⎞15−t⎢⎥()ee−−ete⎜⎟+e+⎜⎟te+⎣⎦24⎝⎠48⎝⎠28⎡1⎤⎡1⎤⎢⎥⎢⎥故xA′=x得通解为xA()(tt=exp)C，由ϕ()00==η可得C=0，故xA′=x满⎢⎥⎢⎥⎢⎣0⎥⎦⎢⎣0⎥⎦⎡13tt−⎤⎢()ee+⎥2⎢⎥⎢13tt−⎥足初值条件ϕ()0=η的解为ϕ()te=−()e。⎢4⎥⎢⎥⎢13tt−−⎥()ee⎢⎣2⎥⎦'