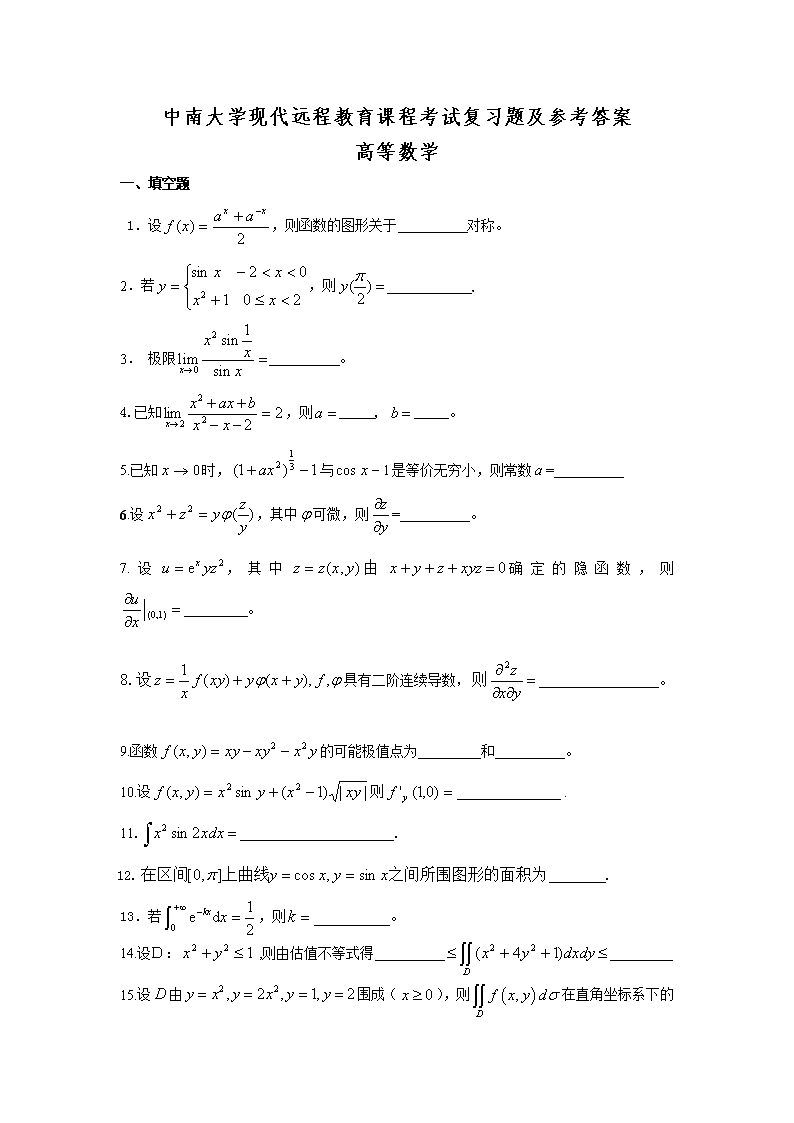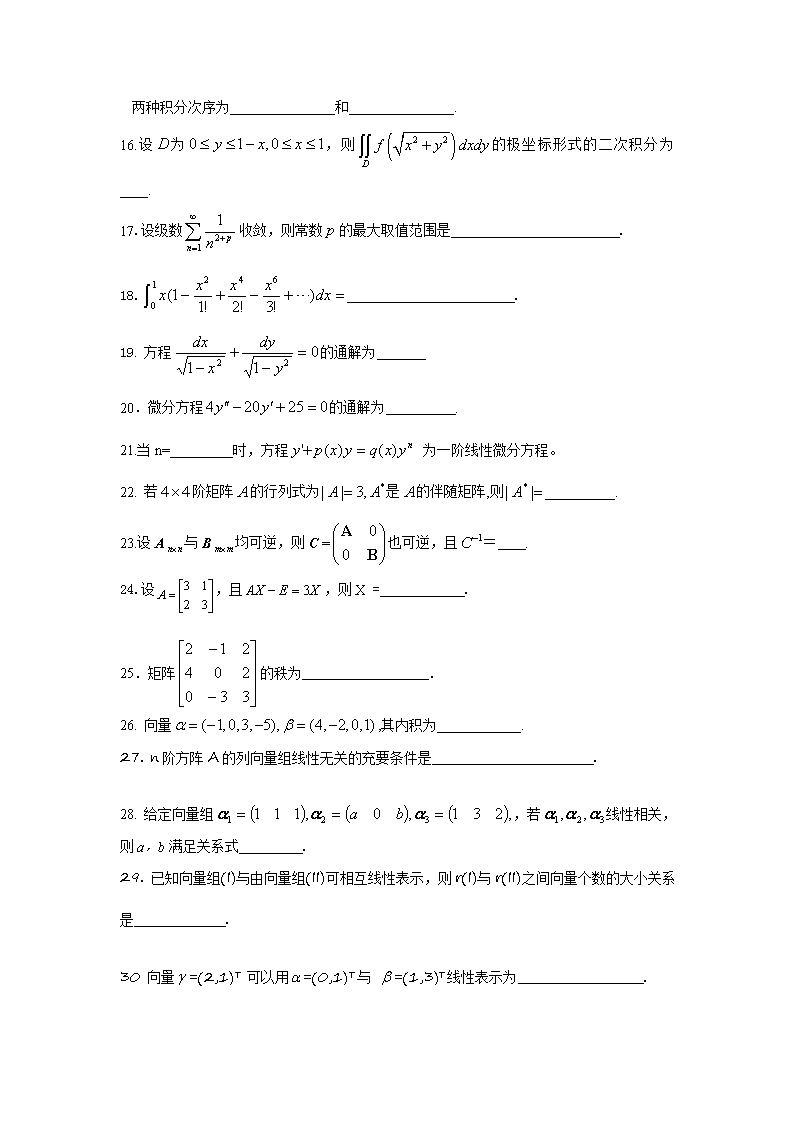高等数学复习题及答案.doc 37页

'中南大学现代远程教育课程考试复习题及参考答案高等数学一、填空题1．设，则函数的图形关于　　　　　对称。2．若，则　　　　　　.3．极限　　　　　。4.已知，则_____,_____。5.已知时，与是等价无穷小，则常数=6.设，其中可微，则=。7.设，其中由确定的隐函数，则 　　　。8.设具有二阶连续导数，则  。9.函数的可能极值点为和。10.设则.11..12..13．若，则。14.设Ｄ：,则由估值不等式得15.设由围成（），则 在直角坐标系下的两种积分次序为_______________和_______________.16.设为，则的极坐标形式的二次积分为____.17.设级数收敛，则常数的最大取值范围是.18..19.方程的通解为20．微分方程的通解为.21.当n=_________时，方程为一阶线性微分方程。22.若阶矩阵的行列式为是的伴随矩阵,则__________.23.设A与B均可逆，则C=也可逆，且＝　　.24.设，且，则X=.25．矩阵的秩为．26.向量,其内积为____________.27.n阶方阵A的列向量组线性无关的充要条件是.28.给定向量组，若线性相关，则a，b满足关系式.29.已知向量组(I)与由向量组(II)可相互线性表示，则r(I)与r(II)之间向量个数的大小关系是.30向量=(2,1)T可以用=(0,1)T与=(1,3)T线性表示为. 31.方程组Ax=0有非零解是非齐次方程组AB=b有无穷组解的条件.32.设A为m×n矩阵,非齐次线性方程组b有唯一解的充要条件是r(A)r(A|b)=.33.已知元线性方程组有解，且，则该方程组的一般解中自由未知量的个数为　　　　　　．34.设是方阵A的一个特征值，则齐次线性方程组的都是A的属于的特征向量.35.若3阶矩阵A的特征值为1，2，-3，则的特征值为.36.设A是n阶方阵，|A|≠0,为A的伴随矩阵,E为n阶单位矩阵，若A有特征值,则必有特征值.37.a,b分别为实对称矩阵A的两个不同特征值所对应的特征向量,则a与b的内积（a,b）=.38.二次型的秩为.39.矩阵为正定矩阵,则的取值范围是_________.40.二次型是正定的,则的取值范围是_____.41.A、B、C代表三事件，事件“A、B、C至少有二个发生”可表示为　　　　.42.事件A、B相互独立，且知则　　　　.43.　若随机事件A和B都不发生的概率为p，则A和B至少有一个发生的概率为　　　　.44.在相同条件下，对目标独立地进行5次射击，如果每次射击命中率为0.6，那么击中目标k次的概率为　　　　　().45.设随机变量X服从泊松分布，且则=.46.设随机变量X的分布密度为，则=.47.若二维随机变量（X，Y）的联合分布律为YX1211/163/162b且X，Y相互独立，则常数=,b=.　　 48.设X的分布密度为，则的分布密度为　　　　　.49.二维随机变量（X，Y）的联合分布律为YX1210.220.3则与应满足的条件是　　　　　，当X，Y相互独立时，＝　　　　.50.设随机变量X与Y相互独立，且令Z=-Y+2X+3，则=.51.已知随机变量X的数学期望.令Y＝2X－3，则=.二、单项选择题1．设，则=（）．A．x　　B．x+1　C．x+2　　　D．x+32．下列函数中，（　）不是基本初等函数．A．　　B．　　C．　D．3.下列各对函数中，（　）中的两个函数相等.　　A.与　　B.与C.与　D.与4.设在处间断，则有（）(A)在处一定没有意义；(B);(即)；(C)不存在，或；(D)若在处有定义，则时，不是无穷小5．函数在x=0处连续，则k=()． A．-2B．-1C．1D．26.若，为无穷间断点，为可去间断点，则（）.（A）1（B）0（C）e（D）e-17．函数的定义域为（   ）．      A．   B．C．       D．8．二重极限（）（A）等于0（B）等于1(C)等于（D）不存在9.利用变量替换，一定可以把方程化为新的方程（ ）．(A)     (B)     (C)     (D)10．若，在内则在内（　）.(A)(B)(C)(D)11.设的某个邻域内连续，且，，则在点处（）.（A）不可导（B）可导，且（C）取得极大值（D）取得极小值 12.设函数是大于零的可导函数，且，则当时，有（）.（A）（B）（C）（D）13.().（A）（B）（C）（D）14.设上具有连续导数，且，则（）.（A）2（B）1（C）-1（D）-215.设上二阶可导，且记，，则有（）.（A）（B）（C）（D）16.设幂级数在处收敛.则此级数在处().（A）绝对收敛（B）条件收敛（C）发散（D）收敛性不能确定17.下列命题中,正确的是（）.（A）若级数的一般项有则有（B）若正项级数满足发散（C）若正项级数收敛，则（D）若幂级数的收敛半径为，则.18.设级数收敛，则级数（）. （A）绝对收敛（B）条件收敛（C）发散（D）敛散性不确定19.微分方程的通解是（）（A）（B）（C）（D）20.设满足微分方程，若，则函数在点（）（A）取极大值；（B）取极小值；（C）附近单调增加；（D）附近单调减少.21.函数在点处的增量满足且，则（D）（A）（B）（C）（D）22.若含有s个向量的向量组线性相关，且该向量组的秩为r，则必有().(A)r=s(B)r>s(C)r=s+1(D)r0）由已知得：，求得=2∴P{X=3}=46.设随机变量X的分布密度为，则=.　　解：由性质即 解得：a=247.若二维随机变量（X，Y）的联合分布律为YX1211/163/162b且X，Y相互独立，则常数=,b=.　　解：∵X，Y相互独立∴P(X=1，Y=1)=P(X=1)·P(Y=1)即：∴a=又∵∴∴b=48.设X的分布密度为，则的分布密度为　　　　　.　　解：∵P{Y≤y}=P(X3≤y)=P(X≤)=Fx()∴Y=X3的分布密度为(y)=，y≠049.二维随机变量（X，Y）的联合分布律为YX1210.220.3则与应满足的条件是　　　　　，当X，Y相互独立时，＝　　　　. 解∵=1∴=1即有=0.5当X，Y相互独立∴P(X=1,Y=1)=P(X=1)P(Y=1)∴=(+0.2)(+)∴=0.250.设随机变量X与Y相互独立，且令Z=-Y+2X+3，则=.解　∵X与Y相互独立，∴D(Z)=D(–Y+2X+3)=D(–Y)+D(2X+3)=(–1)2D(Y)+4D(X)=1+4×2=9。51.已知随机变量X的数学期望.令Y＝2X－3，则=.解　D(Y)=D(2X–3)=4D(X)=4{E(X2)–[E(X)]2}=4(4–12)=12。二、单项选择题1．设，则=（）．A．x　　B．x+1　C．x+2　　　D．x+3解由于，得＝将代入，得=正确答案：D2．下列函数中，（　）不是基本初等函数．A．　　B．　　C．　D．解因为是由，复合组成的，所以它不是基本初等函数．正确答案：B3.下列各对函数中，（　）中的两个函数相等.　　A.与　　B.与C.与　D.与解：A4.设在处间断，则有（）(A)在处一定没有意义；(B);(即)； (C)不存在，或；(D)若在处有定义，则时，不是无穷小答案：D5．函数在x=0处连续，则k=()．A．-2B．-1C．1D．2答案：B6.若，为无穷间断点，为可去间断点，则（）.（A）1（B）0（C）e（D）e-1解：由于为无穷间断点,所以,故.若,则也是无穷间断点.由为可去间断点得.故选(C).7．函数的定义域为（   ）．      A．   B．C．       D．解：z的定义域为：选D8．二重极限（）（A）等于0（B）等于1(C)等于（D）不存在D）解：与k相关，因此该极限不存在9.利用变量替换，一定可以把方程化为新的方程（ ）． (A)     (B)     (C)     (D)解　　z是x，y的函数，从，可得，，故z是u，v的函数，又，故z是x,y的复合函数，故，，从而左边=因此方程变为：选A10．若，在内则在内（　）.(A)(B)(C)(D)解：选(C).11.设的某个邻域内连续，且，，则在点处（）.（A）不可导（B）可导，且（C）取得极大值（D）取得极小值解：因为,则在的邻域内成立,所以为的极小值.故选(D).12.设函数是大于零的可导函数，且，则当时，有（）.（A）（B）（C）（D）解：考虑辅助函数 13.().（A）（B）（C）（D）解：由积分上限函数的导数可得，故选（A）.14.设上具有连续导数，且，则（）.（A）2（B）1（C）-1（D）-2解：因为，故应选（A）15.设上二阶可导，且记，，则有（）.（A）（B）（C）（D）解：依题意,函数在上严格单调减少,且其图形是向上凸的曲线.依据几何图形可得,故选(B).16.设幂级数在处收敛.则此级数在处().（A）绝对收敛（B）条件收敛（C）发散（D）收敛性不能确定解：选（A）.17.下列命题中,正确的是（）.（A）若级数的一般项有则有（B）若正项级数满足发散 （C）若正项级数收敛，则（D）若幂级数的收敛半径为，则.解：由有，因此，从而发散.故选（B）.18.设级数收敛，则级数（）.（A）绝对收敛（B）条件收敛（C）发散（D）敛散性不确定解：因为收敛，即幂级数在处收敛，由Able定理知，幂级数在处绝对收敛，亦即绝对收敛.故选（A）.19.微分方程的通解是（）（A）（B）（C）（D）解：D20.设满足微分方程，若，则函数在点（）（A）取极大值；（B）取极小值；（C）附近单调增加；（D）附近单调减少.解：B21.函数在点处的增量满足且，则（D）（A）（B）（C）（D）解令，得，，，故选（D）。 22.若含有s个向量的向量组线性相关，且该向量组的秩为r，则必有().(A)r=s(B)r>s(C)r=s+1(D)r0，所以=A，因而P(|A)=P(A|A)=1，故选（A）35.离散型随机变量X的分布列为P{X=k}=,k=1,2,3,4.则()　　（A）0.05　（B）0.1　（C）0.2　（D）0.25 解：由概率分布性质可知，常数a应满足，∴a+2a+3a+4a=1，即有a=0.1，故应选（B）。36.设随机变量X的分布函数为则＝（　　）　　（A）　　（B）　　（C）　　（D）解：∵，故应选（C）。37.设随机变量X服从，的值（　　）　　（A）随增大而减小；（B）随增大而增大；　　（C）随增大而不变；（D）随减少而增大.解：∵X～N(,4)∴P[X≤2+]=P，而值不随的变化而变化，∴P{X≤2+}值随增大而不变，故应选（C）。38.设随机变量，则服从()　　（A）　（B）　（C）　（D）解选（D），∵E(Y)=E(aX+b)=aE(X)+b=a+bD(Y)=D(aX+b)=a2D(X)=a2∴Y～N(a+b，a2)。39 .对目标进行3次独立射击，每次射击的命中率相同，如果击中次数的方差为0.72，则每次射击的命中率等于（　　）　　（A）0.1(B)0.2(C)0.3(D)0.4解选（D）；由题意知：X～B(3,p)，而D(X)=3·p·(1–p)=0.72∴p=0.4。40.设随机变量X的概率密度为，则=().　　（A）-1（B）0（C）1（D）以上结论均不正确解选（B）；∵E(X)=，而被积函数为对称区间上的奇函数，∴E(X)=0。三、解答题1.设，已知在处连续可导，试确立并求解，，在处连续，，即。当时，，当时，，当时，，，故。2.设,其中具有二阶连续偏导数,求.解:, .3．设讨论f(x,y)在（0，0）（1）偏导数是否存在。（2）.是否可微。解：（1）同理可得，偏导数存在。（2）若函数f在原点可微，则应是较高阶的无穷小量，为此，考察极限，由前面所知，此极限不存在，因而函数f在原点不可微。4.在过点的所有平面中,求一平面,使之与三个坐标平面所围四面体的体积最小.解:设平面方程为,其中均为正,则它与三坐标平面围成四面体的体积为,且,令,则由,求得.由于问题存在最小值,因此所求平面方程为,且.5. 解：=6．，其中为圆域。解：将区域分为，其中。于是7．设在上连续，求证：。证明由重积分中值定理，，使得，当时，由f的连续性，知，从而有：8.求幂级数收敛区间及和函数：解：，所以，，. 当时，级数成为，由调和级数知发散；当时，级数成为，由交错级数的Leibniz判别法知此级数是收敛的.所以收敛区间为.设，则，所以，.9．求解解原方程可化为，两边积分得，即。由得，故即为所求。10．求解.解原式可化为，令，得，即,两边积分得，即，，由得，故所求特解为。11．求解满足解特征方程为，，故通解为，由得，故为所求特解。12．求解满足解对应的齐次方程的通解为，设特解为代入原方程得，故原方程通解为，由得 ，。13．设二阶常系数线性微分方程的一个特解为，试确定，并求该方程的通解.解将，，，代入原方程得，故，方程为，故通解为。14．计算下列行列式，解：15．计算下列行列式解：16．证明：证： 17．设AX+E=A2+X，且A=，求X.解：由AX+E=A2+X，得(A–E)X=A2–E，而A–E可逆，故X=A+E=.18．已知矩阵，求常数a，b．解因为所以，得b=2．19．    将向量表示成的线性组合：（1）解：设，按分量展开得到求解得到，即20．问，取何值时，齐次方程组有非零解？解：齐次方程组有非零解的必要条件是系数行列式等于零，故即或齐次方程组有非零解。21．设线性方程组 试问c为何值时，方程组有解？若方程组有解时，求一般解。解可见，当c=0时，方程组有解。且原方程组的一般解为（x3是自由未知量）22.求一个正交变换化下列二次型为标准型：（1）解：对应的矩阵为，特征值为正交矩阵为，标准型为23 ．某工人看管甲、乙、丙3台机器，在1小时内，这3台机器不需照管的概率分别为0.8，0.9，0.6，设这三台机器是否需照管是相互独立的，求在1小时内　(1)有机床需要工人照管的概率；(2)机床因无人照管而停工的概率.解：(1)设Ai表示“甲、乙、丙三台机床无需照管”i=1,2,3，则有机床需要工人照管的事件为，因而=0.568(2)以B表示“机床因无人照看而停工”=0.2×0.1×0.6+0.2×0.9×0.4+0.8×0.1×0.4+0.2×0.1×0.4=0.12424．设随机变量X的分布密度为求(1)常数A；(2)X的分布函数；.　解：(1)由性质即：∴A=(2)由(1)知f(x)=∴F(x)=(–∞