《信号与系统》第三版 (段哲民 著) 课后习题答案-西北工业大学出版社 241页

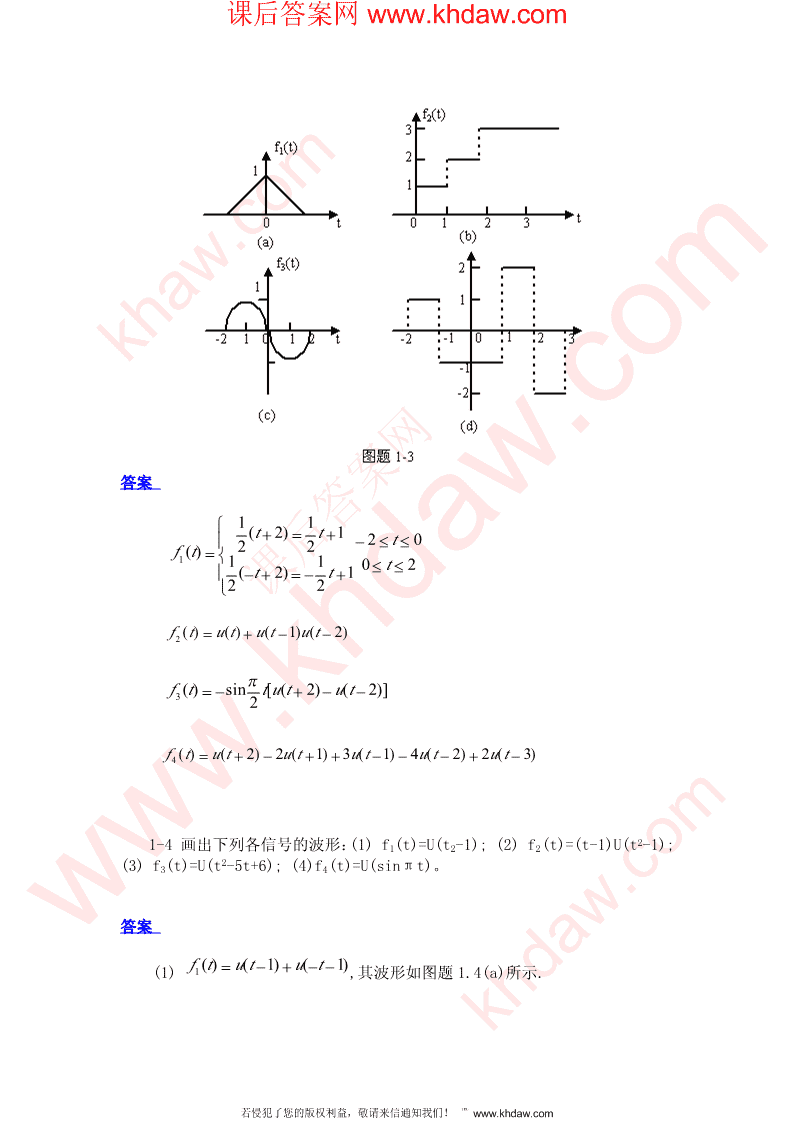
'欢迎光临阳光大学生网,提供最全面的大学生课后习题答案和复习试题免费下载，http://www.sundxs.com/阳光大学生网我们希望呵护您的眼睛，关注您的成长，给您一片绿色的环境，欢迎加入我们，一起分享大学里的学习和生活感悟，免费提供:大学生课后答案，大学考试题及答案，大学生励志书籍。 第一章习题1-1画出下列各信号的波形：(1)f-t-1(t)=(2-e)U(t);(2)f2(t)=etcos10πt×[U(t-1)-U(t-2)]。答案ft)(（1）1的波形如图1.1（a）所示.2πT==2.0s(2)因cos10πt的周期10π,故f2(t)的波形如图题1.1(b)所示.1-2已知各信号的波形如图题1-2所示，试写出它们各自的函数式。答案ft)(=t[ut)(−u(t−1)]+u(t−)11ft)(=−(t−1)[ut)(−u(t−1)]2ft)(=(t−2)[u(t−)2−u(t−3)]31-3写出图题1-3所示各信号的函数表达式。 课后答案网www.khdaw.comkhaw.com答案⎧11(t+)2=t+1⎪−2≤t≤0ft)(=⎨221110≤t≤2⎪(−t+)2=−t+1⎩22f()t=u(t)+u(t−1)u(t−2)2πft)(=−sint[u(t+)2−u(t−2)]32f4(t)=u(t+2)−2u(t+1)+3u(t−1)−4u(t−2)+2u(t−3)1-4画出下列各信号的波形：(1)f1(t)=U(t2-1);(2)f2(t)=(t-1)U(t2-1);(3)f(t)=U(t2-5t+6);(4)f(t)=U(sinπt)。34答案ft)(=u(t−)1+u(−t−)1(1)1,其波形如图题1.4(a)所示.khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comft)(=(t−1)[u(t−)1+u(−t−1)]=(t−)1u(t−)1+(t−)1u(−t−)1(2)2其波形如图题1.4(b)所示.f(t)=u(−t+2)+u(t−3)(3)3,其波形如图1.4(c)所示.f(t)=u(sinπt)(4)4的波形如图题1.4(d)所示.khaw.com1-5判断下列各信号是否为周期信号，若是周期信号，求其周期T。ππ2(1)f(t)=2cos(2t−)(1)f(t)=[sin(t−)]124;6;(3)f(t)=3cos2πtU(t)3。答案周期信号必须满足两个条件:定义域t∈R,有周期性,两个条件缺少任何一个,则就不是周期信号了.2πT=s(1)是,3.1π2πf(t)=3×[1−cos(2t−)]T==πs(2)23,故为周期信号,周期khdaw.com2.若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comt〈0ft)(=0,(3)因时有故为非周期信号1-6化简下列各式：td⎡π(⎤)∞dδ(2τ−1)dτ1⎢cos(t+)δ(t)⎥∫[costδ(t)]sintdt（1）∫−∞;(2)dt⎣4⎦;(3)−∞dt。答案tt1111δ(2[τ−1)]dτ=δ(τ−)dτ=u(t−)∫−∞2∫−∞(1)原式=2222khaw.comdπ2[cos•δ(t)]=δ′(t)(2)原式=dt42∞δ′(t)sintdt=[−sin′(t)]=−cos=−1(3)原式=∫−∞t=0t=0∞∞jwt∫cos[ω(t−3)δ(t−2)]dt∫eδ(t+3)dt1-7求下列积分：（1）0;(2)0;∞−2te×δ(t−t)dt∫0(3)0。答案cos[ω2(−3)]=cos(−ω)=cosω(1)原式=∞−j3ω−j3ωe∫δ(t+3)dt=e×0=0(2)原式=0∞e−2tδ(t−t)dt=e−2t0×1=e−2t0∫0(3)原式=01-8试求图题1-8中各信号一阶导数的波形，并写出其函数表达式，其中πf(t)=cos[tU(t)−U(t−5)]32。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com答案khaw.com（a）f1′(t)=2u(t+1)−3u(t)+u(t−2)，f′(t)的波形如图题1。8（d）所示。f′(t)=u(t+1)−2u(t−1)+3u(t−2)−u(t−3)f′(t)（b）2，2的波形如图题1。8（e）所示。πf′(t)=−sin[tu(t)−u(t−5)]+δ(t)3f′(t)（c）2,3的波形如图题1.8（f）所示.1f()1-9已知信号2的波形如图题1-9所示，试画出y(t)=f(t+1)U(-t)的波形。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comkhaw.com答案y(t)=f(t+1)u(−t)的波形如图题1.9(b)所示。t1-10已知信号f(t)的波形如图题1-10所示，试画出信号∫−∞f(2−τ)dτ与信d[f(6−2t)]号dt的波形。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com答案tf(2−t)∫f(2−τ)dτ(1)的波形与−∞的波形分别如图题1.10(b),(c)所示。d[f(6−2t)]khaw.com(2)f(6−2t)的波形与dt的波形分别如图题1.10(d),(e)所示。d[f(6−2t)]=δ(t−2)+δ(t−5.2)−2δ(t−3)且dt1-11已知f(t)是已录制的声音磁带，则下列叙述中错误的是(__)。A.f(-t)是表示将磁带倒转播放产生的信号B.f(2t)表示磁带以二倍的速度加快播放C.f(2t)表示磁带放音速度降低一半播放D.2f(t)表示将磁带音量放大一倍播放答案Ckhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com1-12求解并画出图题1-12所示信号f1(t),f2(t)的偶分量fe(t)与奇分量fo(t)。khaw.com答案11因(f)t=f(t)+f(t)=[f(t)+f(−t)]+[f(t)−f(−t)]式中e02211f(t)=[f(t)+f(−t)],f(t)=[f(t)−f(−t)]。故可画出各待求偶分量e022与奇分量的波形，相应如图题1.12中所示。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comkhaw.com1-13已知信号f(t)的偶分量fe(t)的波形如图题1-13(a)所示，信号f(t+1)×U(-t-1)的波形如图题1-13(b)所示。求f(t)的奇分量fo(t)，并画出fo(t)的波形。答案因ft)(=f(t)+ft)(e0故有ft)(u(−t)=f(t)u(−t)+f(t)u(−t)e0khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com右移1将信号f(t+1)u(−t−1)⎯⎯→⎯f(t−1+1)u(−t−1+1)=f(t)u(−t),f(t)u(−t)的波形如图题1。13(c)所示。又有(f)t(u)−t=(f)t(u−)t−f(t)u(−t)0eft)(u(−t)的波形如图题1.13(d)所示。0因为ft)(是奇函数，关于坐标原点对称，故f(t)ut)(的波形如图题1.13(e)00所示。最后得f(t)=f(t)u(−t)+ft)(u(t)=u(−t−1)−u(t−1)khaw.com000f(t)的波形如图题1.13(f)所示。01-14设连续信号f(t)无间断点。试证明：若f(t)为偶函数，则其一阶导数f′(t)为奇函数；若f(t)为奇函数，则其一阶导数f′(t)为偶函数。答案khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com（1）若f(t)为偶函数，则有f(−t)=f(t).故f(′−)t=−f′(t).故f′(t)为奇函数。(2）若f(t)为奇函数，则有f(−t)=−f(t).故f(′−t)=−f′(t)，即f′t)(=−[f′(−t)]=−[−f′(t)]=f′t)(.故f′t)(为偶函数。1-15试判断下列各方程所描述的系统是否为线性的、时不变的、因果的系统。式中f(t)为激励，y(t)为响应。dy()t=f(t)khaw.com(1)dt(2)y(t)=f(t)U(t)(3)y(t)=sin[f(t)]U(t)(4)y(t)=f(1-t)(5)y(t)=f(2t)(6)y(t)=[f(t)]2t5ty()t=∫−∞f(τ)dτy()t=∫−∞f(τ)dτ(7)(8)答案(1)线性，时不变，因果系统f(t)y(t)(2)线性，时变，因果系统。因为当激励为时，其响应；当激励为f(t−t)y(t)=f(t−t)u(t)0时，其响应为10，但是y(t−t)≠y(t)01，所以系统为时变系统。(3)非线性，时变，因果系统。y(0)=f(1)(4)线性，时变，非因果系统。因为当t=0时有，即系统当前时刻的响应决定于未来时刻的激励，故为非因果系统。(5)线性，时变，非因果系统。f(t)y(t)(6)非线性，时不变，因果系统。因为当激励为时，响应为；当激2kft)(y()t=[kf(t)]励为时，响应为1，但y(t)≠ky(t)1，故该系统为非线性系统。(7）线性，时不变，因果系统。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com(8)线性，时变，非因果系统。t−tτy(t)=e∫−∞f(τ)edτ1-16已知系统的激励f(t)与响应y(t)的关系为，则该系统为(__)。A 线性时不变系统B 线性时变系统C 非线性时不变系统D 非线性时变系统khaw.com答案A1-17图题1-17(a)所示系统为线性时不变系统，已知当激励f1(t)=U(t)时，其响应为y1(t)=U(t)-2U(t-1)+U(t-2)。若激励为f2(t)=U(t)-U(t-2)，求图题117(b)所示系统的响应y2(t)。答案y(t)=u(t)−2u(t−1)+u(t−2)−2[u(t−1)−2u(t−2)+u(t−3)]+22[u(t−3)−2u(t−4)+u(t−5)]−[u(t−4)−2u(t−5)+u(t−6)=u(t)−4u(t−1)+5u(t−2)−5u(t−4)+4u(t−5)−u(t−6)y(t)的波形如图题1.17(c)所示.2khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comkhaw.com1-18图题1-18(a)所示为线性时不变系统，已知h1(t)=δ(t)-δ(t-1),h2(t)=δ(t-2)-δ(t-3)。（1）求响应h(t)；（2）求当f(t)=U(t)时的响应y(t)（见图题1-18(b))。答案（1）ht)(=ht)(−ht)(=δt)(−δ(t−)1−δ(t−)2+δ(t−)312t(2)因(f)t=u(t)=∫−∞δ(τ)dτ，故根据现行系统的积分性有tt(y)t=∫−∞(h(τdτ=−∫∞[δ(τ)−δ(τ−1)−δ(τ−2)+δ(τ−3])dτ=u(t)−u(t−1)−u(t−2)+u(t−3)khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comkhaw.com1-19已知系统激励f(t)的波形如图题1-19(a)所示，所产生的响应y(t)的波形如图题1-19(b)所示。试求激励f1(t)（波形如图题1-19(c)所示）所产生的响应y1(t)的波形。答案用f(t)表示ft)(即1f(t)=f(t+1)−f(t−1)1khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com故ft)(在同一系统中所产生的响应为1y(t)=y(t+1)−y(t−1)1故y(t+),1y(t−),1y(t)的波形分别如图题1.19(d),(e),(f)所示。khaw.com1-20已知线性时不变系统在信号δ(t)激励下的零状态响应为h(t)=U(t)-U(t-2)。试求在信号U（t-1)激励下的零状态响应y(t)，并画出y(t)的波形。答案t因有u()t=∫−∞δ(τ)dτ，故激励u(t)产生的响应为tt(y)t=(h)τdτ=[u(τ)−u(τ−1)]dτ=1∫−∞−∫∞tt∫−∞u(τ)dτ−−∫∞u(τ−1)dτ=khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com⎧0t〈1⎪tu(t)−(t−1)u(t−1)=⎨t−11≤t〈3⎪⎩2t≥3故激励u(t−1)产生的响应为yt)(=y(t−)1=(t−)1u(t−)1−(t−)2u(t−)21y(t)的波形如图题1。20所示。khaw.com1-21线性非时变系统具有非零的初始状态，已知激励为f(t)时的全响应为y1(t)=2e-tU(t)；在相同的初始状态下，当激励为2f(t)时的全响应为y(t)=(e-t+cosπt)U(t)。求在相同的初始状态下，当激2励为4f(t)时的全响应y3(t)。答案设系统的零输入响应为yt)(，激励为f(t)时的零状态响应为y(t)，xf故有−ty()t=y(t)+y(t)=2eu(t)1xf−ty(t)=y(t)+2y(t)=(e+cosπt)u(t)2xf故联解得−ty(t)=(3e−cosπt)u(t)xkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com−ty(t)=(−e−cosπt)u(T)f故得−t−t−tyt)(=yt)(+4yt)(=3e−cosπt+(4−e+cosπt)=(−e+3cosπt)ut)(3xfkhaw.comkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com第二章习题2-1.图题2-1所示电路，求响应u2(t)对激励f(t)的转移算子H(p)及微分方程。khaw.com答案解其对应的算子电路模型如图题2.1（b）所示，故对节点①，②可列出算子形式的KCL方程为⎧⎛11⎞1⎪⎜⎜+⎟⎟u1(t)−u2(t)=f(t)⎪⎝3p⎠p⎨⎪1⎛11⎞−u(t)+⎜++p⎟u(t)=0⎪p1⎜p1⎟2⎩⎝⎠即⎧⎛1⎞⎪⎜p+1⎟u(1)t−u2(t)=pf(t)⎨⎝3⎠⎪2−u(t)+(p+p+1u(t))=0⎩12联解得khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com3u(t)=(f)t=H(p)f(t)22p+4p+4故得转移算子为u(t)32H（p)==2f(t)p+4p+4u2(t)khaw.com对f(t)的微分方程为(2)p+4p+4u（2t）=3f（t）2ddu(t)+4u(t)+4u(t)=3f（t）2222即dtdt2-2图题2-2所示电路，求响应i(t)对激励f(t)的转移算子H(p)及微分方程。答案解其对应的算子电路模型如图2.2（b）所示。故得khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comf（t）10p+10i(t)==f（t）22p+11p+30×2p1+1.0p+2+2p故得转移算子为i(t)10p+10H(p)==2f(t)p+11p+30i(t)对f(t)的微分方程为khaw.com2(p+11p+30)i(t)=(10p+10)f(t)2dddi(t)+11i(t)+30i(t)=10f(t)+10f(t)2即dtdtdt2-3图题2-3所示电路，已知u--C(0)=1V,i(0)=2A。求t>0时的零输入响应i(t)和uC(t)。答案解其对应的算子电路模型如图题2.3（b）所示。故对节点N可列写出算子形式的KCL方程为khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com⎛p13⎞⎜++⎟u(t)=0⎜⎟C⎝2p2⎠又有uc(t)=pi(t)，代入上式化简，即得电路的微分方程为2⎧(p+3p+2)i(t)=0⎪+−⎨i(0)=i(0)=2⎪+−u(0)=u(0)=1khaw.com⎩cc电路的特征方程为2p+3p+2=0故得特征根（即电路的自然频率）为p1=-1，p2=-2。故得零输入响应的通解式为i(t)=Aep1t+Aep2t=Ae−t+Ae−2t1212−t−2ti′(t)=−Ae−2Ae又12+故有i(0)=A1+A2=2(1)+i′(0)=−A−2A12又因有khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comu(t)=iL′(t)c++u(0)=iL′(0)故cL(−A−2A)=1即12即khaw.com−A1−2A2=1(2)式（1）与式（2）联解得A1=5,A2=-3。故得零输入响应为−t−2t(ti)=5e−3eAt≥0又得di(t)d[−t−2t−t]−2tu(t)=L=15e−3e=−5e+6eVt≥0cdtdt解其对应的算子电路模型如图题2.3（b）所示。故对节点N可列写出算子形式的KCL方程为⎛p13⎞⎜++⎟u(t)=0⎜⎟C⎝2p2⎠又有uc(t)=pi(t)，代入上式化简，即得电路的微分方程为2⎧(p+3p+2)i(t)=0⎪+−⎨i(0)=i(0)=2⎪+−u(0)=u(0)=1⎩cc电路的特征方程为khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com2p+3p+2=0故得特征根（即电路的自然频率）为p1=-1，p2=-2。故得零输入响应的通解式为i(t)=Aep1t+Aep2t=Ae−t+Ae−2t1212−t−2t又i′(t)=−A1e−2A2e+故有i(0)=A1+A2=2(1)+khaw.comi′(0)=−A1−2A22-4图题2-4所示电路，t<0时S打开，已知uC(0-)=6V,i(0-)=0。(1)今于t=0时刻闭合S，求t>0时的零输入响应uC(t)和i(t)；（2）为使电路在临界阻尼状态下放电，并保持L和C的值不变，求R的值。答案解（1）t>0时S闭合，故有+−u(0)=Li′(0)=6Vc+−i(0)=i(0)=0t>0时的算子电路模型如图题2.4(b)所示。故得t>0电路的微分方程为khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com111u(t)=(5.2+p)i(t)=(5.2+p)(−pu)=cc4445.212−pu(t)−pu(t)cc416⎛122.5⎞⎜p+p+1⎟uc(t)=0即⎝164⎠2⎧(p+10p+16)u(t)=0c⎪+−khaw.com⎨uc(0)=uc(0)=6⎪+−i(0)=i(0)=0即⎩其特征方程为p2+10p+16=0，故得特征根（即电路的自然频率）为p1=-2,p2=-8。故得零输入响应uc(t)的通解形式为−2t−8tu(t)=Ae+Aec12−2t−8tu′t)(=−2Ae−8Ae又有c12−2t−8t故Cu′(t)=C(−2A1e−8A2e)1−2t−8t−i(t)=(−2Ae−8Ae)=12即4V1−2t−8t−Ae−2Ae1221−2t−8ti(t)=Ae+2Ae12即2+⎧u(0)=A+A=6c12⎪⎨+1⎪i(0)=A1+2A2=0故有⎩2联解得A1-=8,A2=-2。故得−2t−8tu(t)=8e−2eVt≥0ckhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comduc−2t−8ti(t)=−C=4e−4eAt≥0又得dt2-5图题2-5所示电路，（1）求激励f(t)=δ(t)A时的单位冲激响应uC(t)和i(t)；（2）求激励f(t)=U(t)A时对应于i(t)的单位阶跃响应g(t)。khaw.com答案解（1）该电路的微分方程为2dLdLC(i)t+(i)t+(it)=f(t)2dtRdt代入数据并写成算子形式为2(p+5p+4)i(t)=4f(t)=4δ(t)故得4i(t)=δ(t)=2p+5p+4⎛44⎞⎜−⎟⎜33⎟4141+δ(t)=×δ(t)−×δ(t)⎜p+1p+4⎟3p+13p+4⎜⎟⎝⎠khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com⎛4−t4−4t⎞i(t)=⎜e−e⎟U(t)A故得⎝33⎠进一步又可求得uc(t)为di(t)⎛4−t16−4t⎞uc(t)=L=.025⎜−e+e⎟=dt⎝33⎠⎛1−t4−4t⎞⎜−e+e⎟U(t)V⎝33⎠khaw.comt（2）因有U()t=∫−∞δ(τ)dτ，故根据线性电路的积分性有tt⎛4−τ4−4τ⎞g()t=∫−∞i(τ)dτ=∫−∞⎜e−e⎟U(τ)dτ⎝33⎠⎛4−t1−4t⎞⎜1−e+e⎟U(t)A⎝33⎠2-6图题2-6所示电路，以uC(t)为响应，求电路的单位冲激响应h(t)和单位阶跃响应g(t)。答案解电路的微分方程为2dduc+3uc+2u=2f(t)2cdtdt写成算子形式为khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com(p2+3p+2)u(t)=2f(t)c⑴当f(t)=δ(t)V时，有uc(t)=h(t)。故得单位冲击响应为22h(t)=δ(t)=δ(t)=p2+3p+2(p+1p)(+2)2−2δ(t)=δ(t)=p+1p+2khaw.com−t−2t−t−2t2e−2e=2(e−e)U(t)V⑵当f(t)=U(t)V时，有uc(t)=g(t)。故得tt−τ−2τg()t=∫−∞h(τ)dτ=−∫∞(2e−e)U(τ)dτ=t−τ−2τ−τ−2τ2∫(e−e)dτ=(−2e+e+1)+U(t)V02-7求下列卷积积分（1）t[U(t)-U(t-2)]*δ(1-t);(2)[(1-3t)δ’(t)]*e-3tU(t)答案t[Ut)(−U(t−)2]∗δ(t−)1=解⑴原式=(t−)1[U(t−)1−U(t−)3]−3t−3t⑵原式=δ′(t)∗eU(t)−3tδ′(t)∗eUt)(=[−3t′{[]′]}−3teUt)(−3tδt)(−δt)(∗eUt)(=−3t−3t−3eU(t)+δ(t)+3eU(t)=δ(t)khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com2-8已知信号f1(t)和f2(t)的波形如图题2-8(a),(b)所示。求y(t)=f1(t)*f2(t)，并画出y(t)的波形。khaw.com答案f(t)=1+U(t−1)解(a)1−(t+)1f(t)=eU(t+1)2y()t=f(t)∗f(t)=故112khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com[−](t+)11+u(t−1)∗eU(t+1)=∞∞−(τ+)1−(τ+)1∫eU(τ+1)dτ+∫U(t−τ−1)eU(τ+1)dτ=−∞−∞∞t−1−(τ+)1−(τ+)1∫edτ+∫edτ=−1−1⎧,1t<,0−t1+(1−e)U(t)=⎨−tkhaw.com⎩2−e,t≥0y1(t)的波形如图.2.8(c)所示ft)(=sintU(t),ft)(=U(t−)1(b)12,故yt)(=ft)(∗ft)(=sintUt)(∗U(t−)1=212∞∫sinτU(τ)U(t−τ−1)dτ=−∞t−1⎡∫sinτdτ⎤U(t−1)=[1−cos(t−1)U(t−]1)⎢⎣0⎥⎦y2(t)的波形如图.2.8(d)所示2-9图题2-9(a),(b)所示信号，求y(t)=f1(t)*f2(t)，并画出y(t)的波形。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comkhaw.com答案′tf(t)和f(τ)dτ解利用卷积积分的微分积分性质求解最为简便。1∫−∞2的波形分别如图2.9（c）,(d)所示。故t(y)t=(f)t∗f()t=f(′)t∗f(τ)dτ12∫−∞2y(t)的波形如图题2.9(e)所示.2-10.已知信号f1(t)与f2(t)的波形如图题2-10(a),(b)所示，试求y(t)=f1(t)*f2(t)，并画出y(t)的波形。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comkhaw.com答案(y)t=(f)t∗f()t=f(t)∗[−δ(t+1)+δ(t−1)]=解(a).1121−f(t+1)+f(t+1)11y1(t)的波形如图题2.10(c)所示yt)(=ft)(∗ft)(=(b).212f(t)∗[δ(t−1)−δ(t−2)+δ(t−3)]=1f(t−1)−f(t−2)+f(t−3)111y2(t)的波形如图题2.10(d)所示khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com2-11．试证明线性时不变系统的微分性质与积分性质，即若激励f(t)产生的响ddtf(t)y(t)∫f(τ)dτ应为y(t)，则激励dt产生的响应为dt（微分性质），激励−∞t∫−∞y(τ)dτ产生的响应为（积分性质）。答案解（1）设系统的单位冲激响应为h(t)，则有yt)(=ft)(∗ht)(对上式等号两端求一阶导数，并应用卷积积分的微分性质，故有khaw.comdd(y)t=h()t∗f(t)dtdt（证毕yt)(=ft)(∗ht)(（2）对上式等号两端求一次积分，并应用卷积积分的积分性质，故有tt∫−∞(y)τdτ=h(t)∗∫−∞f(τ)dτ（证毕）2-12.已知系统的单位冲激响应h(t)=e-tU(t)，激励f(t)=U(t)。（1）.求系统的零状态响应y(t)。（2）.如图题2-12(a),(b)所示系统，11h(t)=[h(t)+h(−t),h(t])=[h(t)−h(−t)]1222求响应y1(t)和y2(t)（3）.说明图题2-12(a),(b)哪个是因果系统，哪个是非因果系统。答案khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com−t(y)t=(h)t∗(f)t=eU(t)∗U(t)解（1）−tyt)(=(1−e)U(t)yt)(=ft)(∗[ht)(−ht)(=](2)112⎧11⎫U(t)+∗⎨[h(t)+h(−t)−[]h(t)−h(−t)⎬=]⎩22⎭tt⎧e,t<0khaw.com(U)t∗(h−)t=U()t∗eU(−t)=⎨⎩,1t≥0y()t=(f)t∗[h(t)+h(t)=]212⎧1[1[]⎫]U(t)∗⎨h(t)+h(−t)+h(t)−h(−t)⎬=⎩22⎭−tU()t∗h(t)=(1−e)U(t)（3）因f(t)=U(t)为因果激励，但y1(t)为非因果信号，y2(t)为因果信号，故图题2.12(a)为非因果系统，图题2.12(b)为因果系统。−5tf(t)=eU(t)yt)(=sinωtUt)(2-13.已知激励产生的响应为，试求该系统的单位冲激响应h(t)。答案解因有y(t)=f(t)*h(t)，即−5tsinωtU(t)=eU(t)*h(t)对上式等号两端同时求一阶导数，并应用卷积积分的微分性质有[−5t]ωcosωtU(t)=−5eUt)(+δ(t)*h(t)=khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com−5t−5eU(t)*h(t)+h(t)=−5sinωtU(t)+h(t)故得系统的单位冲激响应为h(t)=(5sinωt+ωcosωt)U(t)y′′(t)+3′(t)+2y(t)=f(t)2-14.khaw.com已知系统的微分方程为。（1）.求系统的单位冲激响应h(t)；−tf(t)=eU(t)（2）.若激励，求系统的零状态响应y(t)。答案解（1）其算子形式的微分方程为(2)p+3p+2y(t)=f(t)1y(t)=f(t)2p+3p+2故得f(t)=δ(t)y(t)=h(t)当时，则有。故上式变为11−1h(t)=δ(t)=(+)δ(t)=(p+1)(p+2)p+1p+211−t−2tδ(t)−(δ)t=(e−e)U(t)p+1p+2（2）零状态响应为−t−2t−t()yt=(h)t∗(f)t(=e−e)U()t∗eU(t)=khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com−1t−2t−t(−e+e+te)U(t)2-15.图题2-15所示系统，其中h1(t)=U(t)(积分器)，h2(t)=δ(t-1)（单位延时器），h3(t)=-δ(t)（倒相器），激励f(t)=e-tU(t)。（1）.求系统的单位冲激响应h(t)；（2）.求系统的零状态响应y(t)。答案khaw.comf(t)=δ(t)y(t)=h(t)解（1）当时，，故ht)(=h(t)+h(t)∗h(t)=123Ut)(+δ(t−)1∗[−δt)(=U]t)(−δ(t−)1−t[]()yt=(f)t∗(h)t=eU()t∗U(t)−δ(t−1)=（2）−t−teU(t)∗Ut)(−eUt)(∗δ(t−1)=−t−(t−)1−(1−e)U(t)−eU(t−1)2-16.已知系统的微分方程为2dddy(t)+2(y)t=f(t)+3f(t)+3f(t)2dtdtdt求系统的单位冲激响应h(t)和单位阶跃响应g(t)。答案解（1）系统算子形式的微分方程为2(p+2)y(t)=(p+3p+3)ft)(khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com2p+3p+3y(t)=f(t)故p+2f(t)=δ(t)y(t)=h(t)当时，故得单位冲激响应为2p+3p+31h(t)=δ(t)=(p+1+)δ(t)=p+2p+2−2tδ(′)t+δ(t)+eU(t)khaw.com（2）系统的阶跃响应为t1−2t(g)t=∫h(τ)dτ=(1−e)U(t)+δ(t)−∞22-17.图题2-17所示系统，h1(t)=h2(t)=U(t)，激励f(t)=U(t)-U(t-6π)。求系统的单位冲激响应h(t)和零状态响应y(t)，并画出它们的波形。答案解（1）.求单位冲激响应h(t)。由图题2.17(a)得[ft)(−yt)(∗ht)(]∗ht)(=yt)(21([f)t−(y)t∗U()t]∗U(t)=y(t)即()ft∗(U)t−(y)t∗U()t∗U(t)=y(t)即对上式等号两端求一阶导数有khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com(f)t∗(δ)t−(y)tδ()t∗U(t)=y′(t)(f)t−(y)t∗U(t)=y′(t)即f′t)(−yt)(∗δt)(=y′′t)(再求一阶导数有y(′′)t+y(t)=f′(t)故得系统的微分方程2写成算子形式为(p+1)y(t)=pft)(py(t)=f(t)2故得khaw.comp+1f(t)=δ(t)当时，有y(t)=h(t)。故得单位冲激响应为ht)(=costUt)(h(t)的波形如图题2.17(b)所示（2）.系统的零状态响应为yt)(=ft)(∗ht)(=[Ut)(−U(t−6π)]∗costUt)(=U(t)∗costU(t)−U(t−6π)∗costU(t)=U(t)∗costU(t)−U(t−6π)∗costU(t)=tt−6π∫cosτdτ−∫cosτdτ=sint[U(t)−U(t−6π)]00y(t)的波形如图题2.17（c）所示。1−4th(t)=eU(t)A2-18.图题2-18(a)所示系统，已知2，子系统B和C的单位阶−t−3tgt)(=1(−e)U(t),gt)(=2eUt)(跃响应分别为Bc。（1）求整个系统的单位阶跃响应g(t)；khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com（2）激励f(t)的波形如图题2-18(b)所示，求大系统的零状态响应y(t)。khaw.com答案解（1）系统B的单位冲激响应为dd[−t]−th()t=g(t)=(1−e)U(t)=eU(t)BBdtdt设系统C的单位冲激响应为hC(t)。故大系统的单位冲激响应为ht)(=ht)(∗[h(t)+ht)(]cAB故大系统的单位阶跃响应为t()gt=∫(h)τdτ=g()t∗[h(t)+h(t)]=cAB−∞−3t⎡1−4t−t⎤2eU(t)∗eU()t+eU(t)=⎢⎥⎣2⎦−3t−4t−3t−teUt)(∗eU(t)+2eU(t)∗e(t)=−t−4t(e−e)U(t)（查卷积积分表）（2）激励f(t)的函数表达式为ft)(=Ut)(−2U(t−)2+U(t−)4+2δ(t−)4大系统的单位冲激响应为khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comdd−t−4td[−t−4t](h)t=(g)t=(e−e)U(t)=eU(t)−eU(t)=dtdtdt−t−4t−4t−tδ()t−eU(t)−δ(t)+4eU(t)=(4e−e)U(t)故零状态响应为t()yt=(h)t∗(f)t=∫−∞h(τ)dτ∗f′(t)=khaw.comg(t)∗[δ(t)−2δ(t−2)+δ(t−4)+2δ′(t−4)]=−t−4t[−(t−)2−(4t−)2](e−e)U(t)−2e−eU(t−2)+[−(4t−)4−(t−)4]7e−eU(t−4)−2t2-19.已知系统的单位阶跃响应为g(t)=(1-e)U(t)，初始状态不为零。−t−t（1）若激励f(t)=eU(t)，全响应y(t)=2eU(t)，求零输入响应yx(t)；（2）若系统无突变情况，求初始状态yx(0-)=4，激励f(t)=δ′(t)时的全响应y(t)。答案解（1）.系统的单位冲激响应为−2th(t)=g′(t)=2eU(t)故零状态响应为−t−2t−t−2ty()t=(f)t∗h(t)=eU(t)∗2eU(t)=(2e−e)U(t)f故得系统的零输入响应为yt)(=y(t)−y(t)=xfkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com−t−t−2t−2t2eUt)(−2eU(t)+2eU(t)=2eU(t)故得系统的初始状态为−+y(0)=y(0)=2xxf(t)=δ′(t)（2）.当的零状态响应为−2t(y)t=(δ)′t∗(h)t=δ()t∗h(′t)=h′(t)=2δ(t)−4eU(t)fkhaw.com根据零输入响应的线性性质，当yx(0-)=4的零输入响应为[−2t]−2ty(t)=22eU(t)=4eU(t)x−故得激励f(t)=δ′(t)，初始状态yx(0)=4时的全响应为−2t−2t(y)t=y(t)+y(t)=2δ(t)−4eU(t)+4eU(t)=2δ(t)fx2-20.已知系统的微分方程为y′(t)+2y(t)=f(t),系统的初始状态−−ty(0)=2f(t)=eU(t)yt)(.(1)求激励1时的全响应1;(2)求激励−tf2(t)=5eU(t)时的全响应y2(t).答案解将微分方程写成算子形式为(p+2)y(t)=f(t)1y(t)=f(t)p+2故(1)求系统的零输入响应yx(t).系统的特征方程为p+2=0,故特征根为p=−2.故得零输入响应的通解形式为−2ty(t)=Aex−−y(0)=y(0)=A=2故xkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com故得系统的零输入响应为−2ty(t)=2eU(t)x−t(1)求激励f1(t)=eUt)(时的零状态响应yf(t).当激励f1(t)=δ(t)时,有y(t)=h(t),故得单位冲激响应为1−2th(t)=δ()t=eU(t)p+2khaw.com故得系统的零状态响应为−t−2t−t−2t()yt=()ft(∗)ht=e(U)t∗eU()t=(e−e)U(t)f1故得系统的全响应为−2t−t−2ty()t=y(t)+y(t)=2eU()t+(e−e)U(t)=1xf−2t−t(e+e)Ut)(−tf(t)=5eU(t)(1)激励2时的零状态响应为−t−2ty(t)=5(e−e)U(t)f故得此时系统的全响应为−2t−t−2ty()t=y(t)+y(t)=2eU(t)+(5e−e)U(t)=2xf−t−2t(5e−3e)Ut)(y′′(t)+3y′(t)+2y(t)=f′(t)+3f(t)2-21.已知系统的微分方程为系统零输++y(0)=1y′(0)=2入响应的初始值为x,x，激励−3tf(t)=eUt)(.试求系统的全响应y(t),并求全响应的初始值y(0+).答案khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com解（1）求零输入响应yx(t)。将微分方程写成算子形式为2(p+3p+2)y(t)=(p+3)ft)(p+3y(t)=f(t)2p+3p+2故系统的特征方程为2p+3p+2=0y(t)故得特征根为pkhaw.com1=-1,p2=-2。故得零输入响应x的通解形式为−t−2ty(t)=Ae+Aex12−t−2ty′(t)=−Ae−2Ae又x12+⎧⎪yx(0)=A1+A2=1⎨+⎪⎩y′(0)=−A−2A=2故有x12A=4A=−3联解得1,2。故得零输入响应为−t−2ty(t)=(4e−3e)U(t)x(2)求单位冲激响应h(t)p+3p+3h(t)=δ(t)=δ(t)=2p+3p+2(p+1)(p+2)2−1−t−2tδ(t)+δ(t)=(2e−e)U(t)p+1p+2（2）求零状态响应yf(t).−3t[−2t−2t]y()t=(f)t∗h()t=eU(t)∗2e−eU(t)=f−3t−t−3t−2teU(t)∗2eU()t−eU()t∗eU(t)=khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com1−3t−t−3t−2t2(−)(e−e)U()t+(e−e)U(t)=2−t−2t(e−e)U(t)（2）全响应为y(t)=y(t)+y(t)=xf−t−2t−t−2tkhaw.com(4e−3e)Ut)(+(e−e)Ut)(=−t−2t(5e−4e)U(t)+y(t)y(0)=1y(t)（2）全响应的初始值为。全响应的一阶导数为−t−2ty′(t)=(−5e+8e)U(t)+y′(0)=−5+8=3故khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com第三章习题ft)(3.1图题3.1所示矩形波，试将此函数用下列正弦函数来近似ft)(=Csint+Csin2t+…+Csinnt12n。khaw.comf(t)1πt−π0-13.1答案任一函数在给定的区间内可以用在此区间的完备正交函数集表示，但若只取函数集中的有限项，或者正交函数集不完备，则只能得到近似的表达式。π∫f(t)sinntdt−πC=nπ2∫sinntdt−π(−π,π)由于分母与分母中的被积函数在区间内是偶函数，故有khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comππ1−∫sinntdtcosnt20nnC===[(−1)−1]nπsin2ntdt1⎡1⎤nπ∫t−sin2nt0⎢⎥2⎣2π⎦0故得44C=−,C=,0C=−,C=,0…1234π3πkhaw.comf(t)3.2求图题3.2（a）所示周期锯齿波的傅里叶级数。f(t)1......t-2T-T0T2T3T3.2(a)答案"""ft)(f(t)f(t)将求导得，的波形分别如图3.2（b），（c）所示。f′(t)f′′(t)1/T-2T-T0T2Ttt-2T-T0T2T............(1)(1)(1)(1)(1)(c)(b)3.2""f(t)于是得的傅立叶系数为khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com•TTA(jnΩ)=22f""(t)e−jnΩtdt=22−δ"te−jnΩtdt=2∫−T∫−T()TT22TTT−2∫2[e−jnΩ×0δ"(t)+jnΩe−jnΩ×0δ(t)]dt=−2∫2δ"(t)dt−2jnΩ∫2δ(t)dt=TTTT−T−T−2222jnΩ2jnΩ0−=−TTf(t)故得的傅立叶系数为khaw.com2jnΩ••A(jnΩ)−2−212T−An==−===22(jnΩ)(jnΩ)jnΩTjn2πjnπ(n≠0)2T2T1A=f(t)dt=tdt=10∫0∫0TTTft)(于是得的傅立叶级数为1∞A1∞•11∞1jnΩt0jnΩtjnΩtf(t)=∑Ane=+∑Ane=+∑(−)e2n=−∞22n=−∞22n=−∞jnπn≠0n≠0∞1111111=−(sinΩt+sin2Ωt+sin3Ωt+…)=−∑sinnΩt2π232πn=1nf(t)3.3求图题3.3（a）所示信号的傅里叶级数。f(t)1......t-T-T/20T/2T3.3(a)khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com答案"""""：f(t)，f(t)的波形如图3.3(b),(c)所示。于是得f(t)的傅立叶系数为khaw.comf′(t)f(t)′′2/T2/T............tt-T-T/20T/2T-T-T/20T/2T(1)(1)(1)(c)(b)3.32πΩ=•2TT2T⎡22TT⎤AjnΩ=2f""te−jnΩtdt2δt−δt−−δ"t−e−jnΩtdt2()()()()()∫T=∫T⎢⎥T−2T−2⎣TT22⎦44n2jnΩn=−(−1)−(−1)22TTTf(t)故得的傅立叶系数为••A2(jnΩ)1[nj]nAn==(−1)−1+(−1)n≠0222(jnΩ)nπnπ又T2T221A=f(t)dt=2tdt=0∫0∫0TTT2f(t)故得的傅立叶级数为khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comA1∞•0jnΩtf(t)=+∑Ane22n=−∞n≠0f(t)T=1s3.4khaw.com求图题3.4(a)所示信号的傅里叶级数，。f(t)E......t-T0T2T3T3.4(a)答案"""""f(t)，f(t)的波形如图题3.4（b）,(c)所示。于是得f(t)的傅立叶系数为f′(t)πEcosπtf′′(t)πE2(πE)............-T0T2Ttt2−πE−πft)((c)(b)3.4•T22""−jnΩt2T[2]−jnΩtA1(jnΩ)=∫Tf(t)edt=∫0−2πEδ()t−πf(t)edtT−T2khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com2T−jnΩt22T−jnΩt4πE2•=∫0−2πEδ(t)edt−π∫0−f(t)edt=−πAnTTT其中•2T−jnΩtAn=∫−f(t)edtT0•f(t)f(t)为的傅立叶系数。故的傅立叶An系数可求得如下：khaw.com2••4πE2•(jnΩ)An=A2(jnΩ)=−πAnT即[22]•4πEπ+(jnΩ)An=T今T=1s故2πΩ==2πT代入上式得•[222]π−4πnAn=4πE故得•4EAn=−2π(4n−1)f(t)于是得的傅立叶级数为khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com1∞•1∞4E∞2EjnΩtjn2πtjn2πtf(t)=∑Ane=∑−2e=∑−2e2−∞2−∞π(4n−1)−∞π(4n−1)3.5khaw.com设f(t)为复数函数，可表示为实部fr(t)与虚部fi(t)之和，即(f)t=f(t)+jf(t)f()t⇔F(jω)ri，且设。证明：1⎡•⎤F[f(t)=]F(jω)+F(−jω)r2⎢⎣⎥⎦1⎡•⎤F[f(t)=]F(jω)−F(−jω)i2j⎢⎣⎥⎦其中••⎡⎤F(−jω)=Ff(t)⎢⎥⎣⎦答案因ft)(=f(t)+jft)((1)ri故•(f)t=f(t)−jf(t)(2)rikhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com式（1）+式（2）得1⎡•⎤f(t)=f(t)+f(t)r2⎢⎥⎣⎦式（1）-式（2）得1⎡•⎤f(t)=f(t)−f(t)i2j⎢⎥⎣⎦故得khaw.com1⎡•⎤F[f(t)=]F(jω)+F(−jω)r2⎢⎣⎥⎦1⎡•⎤F[f(t)=]F(jω)−F(−jω)i2j⎢⎥⎣⎦f(t)F(jω)3.6求图题3.6所示信号的。f(t)Aτt−τ0-A3.6答案khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comττττωτjωωτ−jωωτ⎡jω−jω⎤F(jω)=AτSa()e2−AτSa()e2=AτSa()⎢e2−e2⎥=222⎣⎦2ωτ⎡ωτ⎤sin()sin()2ωτωτ⎢2⎥22ωτ2jAτsin()=2jAτ⎢⎥=jωAτSa()ωτ22ωτ2⎢⎥2⎢⎣2⎥⎦故khaw.com22ωτF(jω)=AτωSa()2f(t)F(jω)3.7求图题3.7所示信号的频谱函数。f(t)1t−2/102/13.7答案方法一用时域积分性质求解。因有"f(t)=G(t)1khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com故"ωf()t⇔G(jω)=Sa()12又因有tt"f()t=f(τ)dτ=G(τ)dτ∫−∞∫−∞1故得khaw.comωSa()G1(jω)2(Fjω)=πG(jω)δ(ω)+=πδ(ω)+1jωjω方法二用卷积性质求解。因有(f)t=G(t)∗U(t)1故得ωSa()ω⎡1⎤2F(jω)=Sa()×⎢πδ(ω)+⎥=πδ(ω)+2⎣jω⎦jωft)(F(jω)3.8求图题3.8所示信号的。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comf(t)1t-3-2-101233.8答案方法一因khaw.comft)(=G(t+)2+G(t−2),22又有ωτG(t)⇔τSa()τ2取ωτ=ω2故得τ=2故G(t)⇔2Sa(ω)2j2ωG2(t+2)⇔2Sa(ω)e−j2ωG(t−2)⇔2Sa(ω)e2故得khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comj2ω−j2ωF(jω)=2Sa(ω)e+2Sa(ω)e=4cos2ω•Sa(ω)方法二因有f()t=G(t)∗δ(t+2)+G(t)∗δ(t−2)22故j2ω−j2ωkhaw.comF(jω)=2Sa(ω)e+2Sa(ω)e=4cosω2•Sa(ω)f(t)⇔F(jω)3.9设。试证：∞1∞)1(F0()=∫f(t)dt　；　　)2(f)0(=∫F(jω)dω−∞2π−∞答案（1）因有∞−jωtF(jω)=∫f(t)edt−∞取ω=0，则得∞F(0)=∫f(t)dt−∞（2）因有1∞jωtf(t)=∫F(jω)edω2π−∞取t=0，则得khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com1∞f(0)=∫F(jω)dω2π−∞f(t)⇔F(jω)3.10已知，求下列信号的傅里叶变换。khaw.com(1)tf(2t)(2)(t−2)f(t)df(t)(3)(t−2)f(−2t)(4)tdt)5(f1(−t)(6)1(−t)f1(−t)(7)f(2t−5)(8)tU(t)答案（1）因有1ωf(2t)⇔F(j)22又有d⎡1ω⎤1"ω−jtf(2t)⇔F(j)=F(j)⎢⎥dω⎣22⎦22故1"ωtf(2t)⇔jF(j)22"(2()t−2)f(t)=tft)(−2ft)(⇔jF(jω)−2F(jω)khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com1d⎡ω⎤1ω(3)(t−2)f(−2t)=tf(−2t)−2f(−2t)⇔jF(−j)−2×F(−j)⎢⎥2dω⎣2⎦22故1"ωω(t−2)f(−2t)⇔jF(−j)−F(−j)222(4)因有dF(jω)khaw.com−jtf(t)⇔dω则有df(t)d−jt⇔[jωF(jω)]dtdω故df(t)["]t⇔−ωF(jω)+F(jω)dt(5)f(1−t)=f[−(t−1)]因有−jω×1f(t−1)⇔F(jω)e故有−jωf1(−t)=f[−(t−)1]⇔F(−jω)e(6)1(−t)f1(−t)=f1(−t)−tf1(−t)−jω⎧d−jω⎫"−jω⇔F(−jω)e−⎨j[F(−jω)e]⎬=−jF(−jω)e⎩dω⎭khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com5⎡5⎤1ω−jω(7)f(2t−5)=f2(t−)⇔F(j)e2⎢⎥⎣2⎦22d⎡1⎤"1(8)tU(t)⇔j⎢πδ(ω)+⎥=πjδ(ω)−2dω⎣jω⎦ωkhaw.comf(t)F(jω)3.11求图题3.11（a）所示信号的。f(t)Et3.11(a)答案⎡1⎤f(t)=EsinΩtU(t)−U(t−)⎢⎥⎣2⎦2πΩ=T"""f(t)，f(t)的波形如图题3.11（b），（c）所示。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comf′(t)f′′(t)EΩ(EΩ)(EΩ)tt0T/22−EΩ−EΩ(c)(b)3.11故有khaw.com""2⎡T⎤(f)t=−Ω(f)t+EΩδ(t)+δ(t−)⎢⎥⎣2⎦故有T⎡−jω⎤(j)ω2F(jω)=−Ω2F(jω)+EΩ1+e2⎢⎥⎣⎦故得TEΩ−jωF(jω)=(1+e2)22Ω−ωf(t)F(jω)3.12求图题3.12所示信号的。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comf(t)21t013.12(a)答案f(t)f(t)f(t)将khaw.com分解为1与2的叠加。即ft)(=ft)(+ft)(12"如图题3.12（b），（c）所示；f2t)(的波形如图题3.12（d）所示，故得11ω−jω(Fjω)=F(jω)+F(jω)=3πδ(ω)+Sa()e212jω2f(t)f(t)121.51tt010(a)(b)f(t)f2′(t)20.51t1-0.501t(c)(d)3.123.13求下列各时间函数的傅里叶变换。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com11n(1)(2)−(3)t2πtπt答案1（1）方法一由于为奇函数，故t⎡1⎤∞1F⎢⎥=−2j∫0sinωtdt⎣t⎦tkhaw.com今⎧πω>0∞sinωt⎪2∫dt=⎨0tπ⎪−ω<0⎩2故⎡1⎤⎧−jπω>0F⎢⎥=⎨⎣t⎦⎩jπω<0又得⎡1⎤⎧−j1ω>0F⎢⎥=⎨⎣πt⎦⎩j1ω<0即⎡1⎤F=−jsgn(ω)⎢⎥⎣πt⎦2sgn(t)⇔jω方法二利用傅立叶变换的对称性求解。因已知有，故有11jsgn(t)⇔2ωkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com故112πjsgn(−ω)⇔2t故得1⇔−jsgn(ω)πt（2）因khaw.com11"−=()2πtπt故⎡1⎤[]⎧ω,ω>0F⎢2⎥=jω−jsgn(ω)=ωsgn(ω)=⎨=ω⎣πt⎦⎩−ω,ω<0（3）因有1⇔δ(ω)2π根据频域微分性质有n1(n)(−jt)•⇔δ(ω)2π故得nn(n)t⇔2πjδ(ω)khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comf(t)(Fjω)=a(ω)−jb(ω)a(ω)3.14已知图题3.14(a)所示信号的频谱函数,b(ω)ω和均为的实函数。试求xt)(=[f(t+1)+f(t−1)]cosωtX(jω)f(t)=ft)(+f(−t)000的频谱函数。0，其波形如图题3.14(b)所示。khaw.comf(t)f(t)EEtt-101(a)(b)3.14答案x(t)=f(t+1)cosωt+f(t−1)cosωt0000今(f)t⇔(Fjω)=a(ω)−jb(ω)故(f)−t⇔(F−)jω=(a−)ω−jb(−ω)=a(ω)+jb(ω)(f)t⇔F(jω)=Fjω)+F(−jω)=2a(ω)00jω−jωf(t+1)+f(t−1)⇔2a(ω)e+2a(ω)e=4aω()cosω00khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com故得1X(jω)={4a(ω)cosω∗2π[(δω+ω)+δ(ω−ω)]}002π=2ωa(ω+)cos(ω+ω)+2ωa(ω−)cos(ω−ω)0000khaw.comF(jω)3.15已知的模频谱与相频谱分别为F(jω)=2[U(ω+3)−U(ω−3)]3ϕ(ω)=−ω+π2F(jω)f(t)f(t)=0求的原函数即时的t值。答案33−jω−ωF(jω)=F(jω)ejϕ(ω)=2[U(ω+3)−U(ω−3)]e2e−jπ=−2G(ω)e26因有⎛ωτ⎞Gτ(t)↔τSa⎜⎟⎝2⎠故khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com6⎛6t⎞3()G6(ω)↔Sa⎜⎟=Sa3t2π⎝2⎠π故6−2G(ω)↔−Sa()3t6π故3khaw.com−ω6⎡⎛3⎞⎤−2G(ω)e2↔−Sa3t−6⎢⎜⎟⎥π⎣⎝2⎠⎦故得6⎡⎛3⎞⎤f(t)=−Sa⎢3⎜t−⎟⎥π⎣⎝2⎠⎦f(t)3.16求下列各频谱函数所对应的时间函数。21(1)ω(2)2ω(3)δ(ω−2)(4)2cosωaω5(5)eU(−ω)(6)6πδ(ω)+(jω−2)(jω+3)答案khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com（1）22"ω=−(jω)×1⇔−δ(t)故"ft)(=−δ(t)（2）因有khaw.com21111jωF(jω)==−•=−•2ωjωjω2jω故根据时域积分性得1t11f(t)=−∫−∞sgn(τ)dτ=−tsgn(t)=−t222（3）因有1⇔2πδ(ω)则有1⇔δ(ω)2π故有1j2te⇔δ(ω−2)2π得1j2tf(t)=e2πkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com（4）因有cos1t⇔π[δ(w−)1+δ(w+)1]则有1cos1t⇔δ(ω−1)+δ(ω+1)π故khaw.com12π×cosω⇔δ(t−1)+δ(t+1)π即2cosω⇔ft)(=δ(t−)1+δ(t+)1aw（5）F(jω)=eU(−ω)的图形如图题3.16所示，F(jω)eαωU(−ω)1ω03.16故得1∞jωt10aωjωt1f(t)=∫−∞F(jω)edω=∫−∞eedω=,−∞0xf（3）全响应：221h(t)=4-6在图题4-6所示系统中，f(t)为已知的激励，πt，求零状态响y(t)应。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com答案1F[h()]t=H(jω)=[−jπsgn(ω)]=−jsgn(ω)解：π所以：(Y)jω=(Fj)ωH(jω)H(jω)=F(jω)[−sgn(ω)sgn(ω)]=−F(jω)khaw.comy(t)=−f(t)所以：ft)(4-7图题4-7(a)所示系统，已知信号如图题4-7(b)所示，f(t)=cosωtf(t)=cos2ωty(t)Y(jω)10，20。求响应的频谱函数。答案(x)t=f(t)f(t)解：111⎧(ω+ω0)τ(ω−ω0)τ⎫X(jω)=F(jω)∗F1(jω)=Aτ⎨Sa[+Sa[]⎬所以：2π2⎩22⎭(y)t=x(t)f(t)又：2所以：khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com11⎧(ω+3ω0)τ(ω−ω0)τω−ω0)τ(ω−3ω0)τ⎫Y(jω)=X(jω)∗F2(jω)=Aτ⎨Sa[+Sa[]+Sa[+Sa[]⎬2π4⎩2222⎭H(jω)=G(ω)4-8理想低通滤波器的传输函数2π，求输入为下列各信号时y(t)的响应。sin4πt()1f(t)=Sa(πt);(2)f(t)=khaw.comπt。答案ωτG(t)⇔τSa()τ解：（1）因有：2G(t)⇔2πSa(πω)2πG(ω)⇔Sa(πt)2πF(jω)=G(ω)所以：2πY(jω)=F(ωj)H(jω)=Gω()G(ω)=G(ω)又：2π2π2πy(t)=Sa(πt)所以：sin4πtf(t)==4Sa(4πt)（2）πtF(jω)=G(ω)所以：8π(Y)jω=(F)jω(Hj)ω=G(ω)G(ω)=G(ω)又：8π2π2πy(t)=Sa(πt)所以：24f(t)=20cos100tcos10t4-9图题4-9所示为信号处理系统，已知，理想khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comH(jω)=G(ω)yt)(低通滤波器的传输函数240。求零状态响应。khaw.com答案H(jω)解：的图形如图题4-9（b）所示。24ft)(=20cos100tcos10t=10cos100t+5cos20100t+5cos19900t所以：F(jω)=10π[δ(ω+100)+δ(ω−100)]+5π[δ(ω+20100)+δ(ω−20100)]+5π[δ(ω+19900)+δ(ω−19900)]khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comF(jω)的图形如图题4-9（c）所示。所以：Y(ωj)=F(jω)H(jω)=10π[δ(ω+100)+δ(ω−100)]Y(jω)的图形如图题4-9（d）所示。所以：yt)(=10cos100t,t∈RH(jω)4-10khaw.com在图题4-10(a)所示系统中，为理想低通滤波器的传输函数，其图形如图题4-10(b)所示，ϕ(ω)=0;f(t)=f0(t)cos1000t,−∞>ωm0且0m，H(jω)=G(ω)y(t)理想低通滤波器的2ω0，如图题4-11(b)所示。求响应。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comkhaw.com答案F(jω)=2[π(δω+ω)+δ(ω−ω)]F(jω)解：mm，的图形如图题4-11(c)所示。X(jω)=50π[δω(+ω)+δω(−ω)]X(jω)00，的图形如图题4-11(d)所示。所以：Y(jω)=50[π{δ(ω+ω+)]ω[+δω(−ω+)]ω+[δω(+ω−ω)]+δ[ω−(ω−ω)]}10m0m0m0mY(jω)1的图形如图题4-11(e)所示。所以：Y(jω)=Y(ωj)H(jω)=50π{δω[+ω(−ω)]+δω[−ω(−ω)]}10m0myt)(=50cos(ω−ω)tt∈R所以：0mkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com4-12在图题4-12(a)所示系统中，已知1f(t)=Sa(2t),−∞0时S在2，故可作出t>0时的s域电路模型，如图题5-8（d）所示。故可列写出节点N的KCL方程为khaw.com3−111ss−s+3(++s)U(s)=+=1111ss35=s+322U(s)==+故s(s+2)ss+235−2tu(t)=(−e)U(t)故得22ut()得波形入图题5-8（e）所示。f(t)/V1ΩN3++f(t)01Ω1Fu(t)t---2(a)(b)khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com1S1ΩN2+++1Ω1Fu(t)2V3V---(c)1Ωut()/VN+khaw.com1.51+s3U(t)-s1Ω+−10st---1(d)(e)图题5-8f()t=UtV()5.9图题5-9所示零状态电路，激励，求电路的单位阶跃响应u()t。+ft)(11ut)(FH22-图题5-9答案图题5-9（a）电路的s域电路模型，如图5-9（b）所示。故得khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com21×ss211U(s)=×=212ss+4+ss2u(t)=sin2tU(t)故得+f(t)11ut)(khaw.comFH22-(a)1+s21sU(s)s2-(b)图题5-9()−−−5.10图题5-10所示电路，已知i0=1A，u(0=)1V，u(0=)sintU()tV。u()t求全响应。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com1ΩNi++21f(t)1ΩHFu32--图题5-10答案khaw.com图题5-10（a）电路的s域电路模型，如图题5-10（b）所示，其中1F(s)=2s+1。故可列写节点N的KCL方程为1ΩNi++21f(t)1ΩHFu32--(a)1ΩN+22s+3sFs()1Ω--21U(s)3s+-(b)图题5-1011s3111(+++)U(s)=+−21122ss+12s故123232ss−2s+3s−2s−2s+3s−2−28.255U(s)===+++22222(s+4s+3)(s+1)(s+1)(s+3)(s+1)s+1khdaw.coms+2s+1s+1若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com故得−t−2t12[−t−2t�]u(t)=(−2e+8.2e+cost+sint)U(t)=−2e+8.2e+.0447cos(t−63.43)U(t)55（V）f()t5.11图题5-11(a)所示电路，已知激励的波形如图题5-11(b)所示，()[()−t]()ft=2U−t+2eUtVt=0St≥0u()tkhaw.com。今于时刻闭合，求时的响应。1Ω(ti)+1H1Ω2S−t2eUt)(f(t)-t=0+1Ω1Fu(t)-0t(a)(b)图题5-11答案t<0时S打开，电路已工作于稳态，电感L相当于短路，电容C相当于开路，−2i(0)==1−故有2A，u(0)=1V.。t>0时S闭合，故可作出t>0时s域电路模型，2F(s)=如图5-1（c）所示，其中s+1。对节点①，②列写KCL方程为⎧111121(++)Φ(s)−U(s)=−⎪⎪11s1s+1s⎨11111⎪−Φ(s)+(++s+)U(s)=1+⎪⎩111sss+211U(s)==+22联解得(s+1)s+1(s+1)khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com−t−t−t(u)t=(e+te)U(t)=(1+t)eU(t)故得1Ωi(t)+1H1ΩSf(t)-t=0+1Ω1Fu(t)-khaw.com(a)2−t2eUt)(0t(b)1ΩΦ(s)1①s1Ω+1-②Φ(s)+21+F(s)s-1Ω+U(s)1s--(c)图题5-11f()t=ft()=UtV()u()t5.12图题5-12所示零状态电路，12。求响应。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com+ut)(-1Ω1Ω1F1H++1Ωft)(f2t)(1--图题5-12答案khaw.com图题5-12（a）电路的s域电路模型，如图题5-12（b）所示。故可列写出节点的KCL方程为11(1+1+)Φ(s)−1Φ(s)=12ss−Φ(s)+1(+1+s)Φ(s)=11211Φ(s)=Φ(s)=12联解得s+1，s+1U(s)=Φ(s)−Φ(s)=0故12ut()=0故得khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com+u(t)-1Ω1Ω1F1H++1Ωft)(f2t)(1--(a)1ΩΦ()sΦ()s12khaw.com+Us()-1Ω1ss++1Ω11ss--(b)图题5-12()−tutf()t=10eUt()V5.13图题5-13所示零状态电路，求电压。已知。4Ω2u-1++++f(t)4Ωu11Hu---图题5-13答案图题5-13（a）电路的s域电路模，如图题5-13（b）所示，其中10F(s)=s+1。故可列写khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com出回路的KVL方程为10(4+4)I(s)−4I(s)=12s+1−4I(s)+4(+s)I(s)=2U(s)121U(s)=4[I(s)−I(s)]又112以上三式联立得khaw.com15I(s)=2(s+1)(s+6)15s−1318U(s)=sI(s)==+2又(s+1)(s+6)s+1s+6−t−6t故得ut)(=(−3e+18e)U(t)（V）khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com4Ω2u-1++++ft)(4Ωu11Hu---(a)khaw.com4Ω-2()Us1+++I2(s)+F(s)4ΩU1(s)sU(s)-I1(s)--(b)图题5-13f()t=UtV()u()t5.14图题5-14所示零状态电路，，求2。i1Ωi122H++f(t)1H4Hu21Ω--图题5-14答案khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com图题5-14（a）的电路的s域电路模型，如图5-14（b）所示。故可列出回路的KVL方程为1(1+s)I(s)−2sI(s)=12s−sI(s)+(4s+1)I(s)=0121I(s)=4.02联解得s+2.04.0U(s)=1×I(s)=22khaw.com故s+2.0−0.2tu(t)=4.0eU(t)故得2（V）i1Ωi122H++f(t)1H4Hu21Ω--(a)I1(s)1ΩI2(s)2s++F(s)1s4sU2(s)s1Ω--(b)图题5-145.15图题5-15所示电路t<0时闭合，电路已工作于稳态。今于St=0时刻i()ti()t打开，求St>0时的1和2。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comSi4Ω1i2t=04H+4H4H8Ω20V4Ω-图题5-15答案khaw.comt<0时得去耦合等效电路如图题5-15（b）所示。t<0时S闭合，电路工作−20i1(0)==5−于稳态，电感相当于短路，故有4A，i2(0)=0，−−−i(0)=i(0)+i(0)=5t>012A。时S打开，其对应的s域电路模型如图题5-15（c）所示。故有205I(s)==4s+4s+1512I(s)=I(s)=I(s)=12故2s+15−ti(t)=i(t)=eU(t)12故得2（A）Si4Ω1i2t=04H+4H4H8Ω20V4Ω-(a)khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comS4Ωi1i2t=0i+4H20V4Ω8Ω-(4-4)H(4-4)H(b)I1(s)4ΩI2(s)khaw.comI(s)4s8Ω4Ω-20V+(c)图题5-155.16图题5-16所示电路，t>0时打开，电路已工作于稳态。今于St=0u()t时刻闭合，求St>0时关于的零输入响应、零状态响应、全响应。Si3Ωt=01H++2Ω+12Vf(t)uc1F1Ωu---图题5-16答案khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comt<0时S打开，电路工作于稳态，电感L相当于短路，电容C相当于开路，故有−12i(0)==23+2+1(V)−−u(0)=(2+1)i(0)=6C(V)t>0时S闭合，其s域电路模型如图题5-16（b）所示。故对节点N课列写出KCL方程为−1i(0)+F(s)−khaw.com(+s+1)U(s)=+uC(0)s+3s+3−−i(0)+(s+3)u(0)F(s)CU(s)=+22故(s+2)(s+2)故得令输入响应与零状态响应的像函数为−−i(0)+(s+3)u(0)6s+2086CU(s)===+X222(s+2)(s+2)(s+2)s+212F(s)s123−6−3U(s)====++f2222(s+2)(s+2)s(s+2)s(s+2)s+2故得零输入响应和零状态响应分别为−2tuX(t)=(8t+6)eUt)(（V）−2tu(t)=[3−(6t+3)e]U(t)f（V）故得全响应为−2t(u)t=u()t+u(t)=[3+(2t+3)e]U(t)Xf（V）khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comSi3Ωt=01H++2Ω+12Vf(t)uc1F1Ωu---(a)I(s)3ΩsN--+1+i(0)khaw.com+sF(s)+1ΩU(s)−u(0)C-s--(b)图题5-16()()0−=1−5.17图题5-17所示电路，ft=UtV，uc()V，i(0=)2A，求响应u()t。uc+-i1F++f(t)0.5Ω1Hu--图题5-17答案图题5-17（a）电路的s域电路模型如图题5-17（b）所示。故可列写出回路的KVL方程为khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com111(5.0+)I(s)−5.0I(s)=−=012sss−5.0I(s)+(s+5.0)I(s)=2122(s+2)I(s)=22(s+1)联解得−2U(s)=sI(s)−2=22(s+1)故−tkhaw.com故得ut)(=−2teUt)(uc+-i1F++f(t)0.5Ω1Hu--(a)11ss+-I(s)+s+1I1(s)I2(s)-s-0.5Ω2V+-(b)图题5-175.18已知系统的微分方程为""()"()()"()()yt+5yt+6yt=2ft+8ftkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com()−t()−"−ft=eUty()0=3y(0=)2()ty激励，初始状态为，。求系统的全响应，并指出零输入响应yx()t、零状态响应yf()t。答案对微分方程等号两边同时求拉普拉斯变换，并考虑到拉普拉斯变换得微分性，有2−−−skhaw.comY(s)−sy(0)−y′(0)+5[sY(s)−y(0)]+6Y(s)=2sF(s)+8F(s)−−2s+8(s+5)y(0)+y′(0)Y(s)=F(s)+=Y(s)+Y(s)22fX故s+5s+6s+5s+61F(s)=−−今s+1，y(0)=3，y′(0)=2，代入上式有2s+813s+17Y(s)=×+22s+5s+6s+1s+5s+6故零状态响应为2s+813−41Y(s)=×=++f2s+5s+6s+1s+1s+2s+3−t−2t−3ty(t)=(3e−4e+e)U(t)故得f零输入响应为3s+1711−8Y(s)==+X2s+5s+6s+2s+3−2t−3t故得yX(t)=11(e−8e)U(t)故得全响应为−t−2t−3t(y)t=y()t+y(t)=(3e+7e−7e)U(t)Xfkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com第六章习题6.1图题6.1所示电路，求u(t)对i(t)的系统函数H(s)=U(s)／I(s)。1Ω1F+i(t)C1HLU(t)R2khaw.com_(a)R1+1I(s)LsLU(s)CsR2_(b)图题6.1答案解：图解6.1（a）电路的s域电路模型图解6.1（b）所示。故有⎡⎛1⎞⎤LsR⎜2+⎟⎢⎥⎝Cs⎠Is()R⎢1+⎥=Us()⎢++1⎥LsR2⎢⎣Cs⎥⎦代入数据得2U(s)2s+2s1+Hs()==2I(s)s++s1khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com1F31Ω+C+L1HU1U2(t)R2Ω2--(a)1CsR1khaw.com++LsU(s)U12R2--(b)图题6.2u()tu()t6.2图解6.2（a）所示电路，求2对1的系统函数U(s)2H(s)=U(s)1。答案解：图解6.2（a）所示电路的s域电路模型如图解6.2（b）所示。故有U(s)LsR+22H(s)==U(s)11LsR+2++R2Cs代入数据得2U()ss+2s2H(s)==()2Uss+5s+31khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com−5tht()=5teUt()6.3已知系统的单位冲激响应，零状态响应−5t−5tyt()=Ut()+2eUt()5+teUt()。求系统的激励f(t)。答案5h()s=解：s+5125Y(s)=++khaw.com2ss+5(s+5)故得激励f(t)的像函数为125++2Y(s)ss+5(s+5)311F(s)===++H(s)55ss+5s+5故得3-5t3-5tft()=δ(t)U(t)eU(t)++=δ(t)+(1e+U(t))552s+5H(s)=2(−)6.4已知系统函数s+5s+5，初始状态为y0=0，/()−y0=-2。(1).求系统的单位冲激响应h(t);(2).当激励f(t)=δ(t)时，求系统的全响应y(t)；(3)当激励f(t)=U(t)时，求系统的全响应y(t)。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com答案解:(1)2()s+5−s2−2ss+12H(s)==1+=1++22(2)(2)s+5s+5s+2s+5s+2+1s+1+4故-2t-2t-2t()h(t)=δ(t)-2ecostU)t(+esinU)t(=δ(t)-2ecos2t−2sin2tU)t(（2）系统的微分方程为khaw.com//()/()()///()()yt+2yt+5yt=ft+5ft对上式等号两边同时求拉普拉斯变换，并考虑到拉普拉斯变换的微分性质，有2(−)/−()(−)2sY)s(−sy0−y0+2sY)s(−2y0+5Y)s(=s)s(F+5F①−/(−)今)s(F=1,y(0)=0,y0=−2,代入上式得2s+32(s+1)Y(s)==1−22s+2s+5(s+1)+4故得全响应为-ty)t(=δ(t)-2ecostU)t(1−/−F(s)=,y(0)=,0y(0=)−2（3）将s代入上式①，有2s−2s+512Y(s)==−2×(2)(2)ss+5s+5ss+1+4故得全响应为khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com(−t)y)t(=1−2esin2tU)t(6.5图题6.5所示电路。(1)求电路的单位冲激响应h(t)；u(2)今欲使电路的零输入响应x(t)=h(t)，求电路的初始状态()−−i0u(0)khaw.com和；(3)今欲使电路的单位阶跃响应g(t)=U(t)，求电路的初始状态()−−i0和u(0。)答案解（1）零状态条件下的s域电路模型如图解6.5（b）所示。故根据该图得1U()ss11H(s)====()12(2)Fss+2s+1s+12+s+s故得单位冲激响应为−t()h)t(=teU)t(Vu()t（2）非零状态条件下求零输入响应x的s域电路模型如图6.5（c）所示。故(−)1(−)i0−u0()s11−us=×+u(0)x1ss2+s+skhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com2Ω1HRL++1FU(s)(ft)C--(a)2Ωs(Is)R+khaw.com+1U(s)F(s)s--(b)-i0()2Ωs-+R++1sU)s()t(f1u0(−)-s-(c)i0(-)+2Ωs-+1+1s)s(Us1+--u(0)−s-(d)图解6.5U()s=H(),s依题意要求，应使x即应有khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com−1−i(0)−u(0)s11−1×+u(0)=1(2)sss+12+s+s从而有−−(s+2)(0)u+i(0)=1−−u(0)=0,(0)1i=Akhaw.com（3）非零状态条件下求电路单位阶跃响应g（t）的s域电路模型，如图解6.5（d）所示。故1−1−+i(0)−u(0)ss11−G(s)=×+u(0)1ss2+s+s1G(s)=,依题意要求，应使s即应有1−1−+i(0)−u(0)ss11−1×+u(0)=1sss2+s+s(−)−()从而有(s+2u)0+i0=s+2()−−()故得u0=1V,i0=0U()s2Hs()=Us1()6.6图题6.6所示电路。(1)求；u()t=cos2tU)t(()V,C=1F,u()t(2)若1求零状态响应2；khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comu()tu()t(3)在1不变的条件下，为使响应2中不存在正弦稳态响u()t应，求C的值及此时的响应2。1H++Cu1u2−−khaw.com()a答案s++u1()s1u2()s−Cs−()b解（1）图解6.6（a）电路的s域电路模型如图题6.6（b）所示。故121s+H()s=2=C1221s×s+s+1CsCC+21s+CssU()s=C,=1F,12（2）s+4则22s+1s+1H()s==22s+2s+1(s+1)故khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com2s+1sKKKK111223U()s=Hs()Us=()×=+++21222(s+1)s+4(s+1)(s+1)s+j2s−j2(2)s+1s(2)2K=s+1=−11(2()2)s+1s+45（s=−1）2d⎡(s+1s)(2)⎤16K=s+1⎥=khaw.com12ds⎢(2)(2)25⎣s+1s+4⎦s=−1(2)s+1s3K=(s+J2)=22(s+1)(s+j2s−)(j2)10s=−j2。−53.13K=K=。3210−53.1故得2−t16−t3−j2t−j53.1。3j2tj53.1。u()t=−te+e+ee+ee=25251010⎡⎤⎢38⎛⎞3⎥−t°⎢⎜−te⎟+cos2t53.1(+⎥ut()()V)⎢�����25⎝⎠�������5⎥⎣瞬态响应正弦稳态响应⎦21s+CsU()s=Hs()Us()=×212122s+4s+s+（3）CCu()t由此式可见，欲使2中不存在正弦稳态响应，就必须有212s+=s+,4C故得C=.025F。代入上式有khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.coms.1077−.0077U()s==+22s+8s+4s+4+23s+4−23故得⎡⎤u()t=⎢.1077e−(4+23t−).0077e−(4−23t⎥)U()()tV2�������������⎢⎣瞬态响应⎥⎦6.7图题6.7所示电路。khaw.comU()s2H(s)=U()s(1)求1；(2)求K满足什么条件时系统稳定；(3)求K=2时，系统的单位冲激响应h(t)。11Ω1Ωs++1++sU)s(U)s(U(s)21----图解6.7答案解（1）对节点①列写KCL方程为⎧⎫⎪1⎪⎨1++s⎬δ(s)-sKU()s=U1s()1⎪s+⎪⎩s⎭U()s⎛1⎞δ(s)=⎜1+⎟1⎝s⎠又skhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comU()s=KUs()2以上三式联解得U()sK()2Hs==()2()Uss+3−Ks+11H()s（2）当K＜3时，的极点位于s平面的左半开平面，系统稳定。khaw.com（3）当K=2时，3()2222Hs===2××s2+s+122322⎛1⎞⎛3⎞⎛1⎞⎛3⎞⎜s+⎟+⎜⎟⎜s+⎟+⎜⎟⎝2⎠⎜⎝2⎟⎠⎝2⎠⎜⎝2⎟⎠故得14−t3h(t)=e2sintU(t)()V32s+5H(s)=26.8已知系统函数s+4s+6。(1)写出描述系统响应y(t)与激励f(t)关系的微分方程；(2)画出系统的一种时域模拟图；−/()−−t(3)若系统的初始状态为y(0)=2,y0=1，激励)t(f=eU()t，y()ty()t求系统的零状态响应f，零输入响应x，全响应y(t)。答案Y()ss+5H()s==()2解（1）因Fss+5s+6khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com故得系统的微分方程为//()/()()/()()yt+5yt+6yt=ft+5ft（2）该系统的一种时域模拟图如图题6.8所示。1∫∫5∑f(t)khaw.comy−5−6图解6.8y()t（3）求零状态响应f1F()s=s+1故s+5s+52−31Y=F()()sHs===++f(()2())()()s+1s+5s+6s+1s+2s+3s+1s+2s+3()(−t−2t−3t)()yt=2e−3e+eUt故得fy()t（4）求零输入响应x2系统的特征方程为s+5s+6=0，故得特征根为p1=−2,p2=−.3故得零输入响应的通解形式为()−2t−3tyxt=A1e+A2e/−2t−3t又yx()t=−2A1e−3A2ekhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com{()++()yy0=y0=A+A=2x12/()+/+()y0=y0=−2A−3A=1故有x12A=7,A=−5联解得12故得零输入响应为()(−2t−3t)()(−t−2t−3t)()(−2t−3t)()yt=7e−5eUt+2e−3e+eUt=4e−4eUt+2ex������������自由响应��������瞬态响应Y()sH()s=khaw.com6.9已知系统的框图如图题6.9所示，求系统函数F()s，并画出一种s域模拟图。11∑s+1∑s+2F(s)y(s)1s1s()a答案(ys)111F(s)∑sss−3−12()bkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com⎧⎡()1()⎤11()⎫1()⎨⎢Fs+Ys⎥+Ys⎬=Ys解⎩⎣s⎦s+1s⎭s+2sH()s=32故解得s+3s+s−2其中一种s域模拟如图解6.9（b）所示。khaw.com6.10已知系统的框图如图题6.10所示。Y()ssH()s==()2(1)欲使系统函数Fss+5s+6，试求a，b的值；(2)当a=2时，欲使系统为稳定系统，求b的取值范围；(3)若系统函数仍为(1)中的H(s)，求系统的单位阶跃响应g(t)。s∑(s+1)(s+a))s(y)s(Fb−s图题6.10答案⎡b⎤sF()s−Y()s=Y()s⎢⎣s⎥⎦(s+1s)(+a)解（1）Y()ssH()s==2解得F()ss+(a+1s)+a+(b)ss=22()()s+5s+6s+a+1s+a+b故有khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com⎧a+1=5⎨a+b=6故有⎩解得a=4,b=2.sH()s=2当a=2时，s+3s+2+b故欲系统为稳定系统，就必须有2+b＞0,b＞-2.khaw.com()1Fs=(3)s,故s1111-G()s=Hs()()Fs=×==+22s+5s+6ss+5s+6s+2s+3故得系统的单位阶跃响应为()(−2t−3t())gt=e−eUt6.11已知系统的框图如图题6.11所示。Y()sH()s=F()s(1)求系统函数；(2)欲使系统为稳定系统，求K的取值范围；(3)在临界稳定条件下，求系统的单位冲激响应h(t)。s∑s2+4s+4KF(s)(ys)图题6.11答案khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.coms[F()s+Ys()]×K=Y()s2解（1）s+4s+4Y()sKsH()s==()2()Fss+4−Ks+4解得4−k〉0k〉4（2）欲为稳定系统，则必须有，故。（3）当K=4时，系统为临稳定，即khaw.com4sH()s=2s+4故得临界稳定条件下的单位冲激响应应为h()t=4cos2tUt()()+6.12图题6.12所示为H(s)的零、极点分布图，且知h0=2。求该系统的H(s)。jωp2×j3j2z1p1×−3−2−1oδ−j1z2-j2p×-j33答案图题6.12khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com解()()(2)2()(s−z1s)(−z2)s+2−j1s+2+j1s+2+1s+4s+5Hs=H0=H0()()(=H)0(()2=H)032(s−ps)(−ps−)(p)s+3s−j3s+j3s+3s+9s+3s+9s+27123又有2+s+4s+5h(0)=limsH(s)=limH=20S32s+3s+9s+27即khaw.comh)0(=2故得22(s+4s+5)H(s)=32s+3s+9s+276.13已知系统的微分方程为///()//()/()/()()()yt+5yt+8yt+4yt=ft+3ftY()sH()s=F()s（1）求系统函数；（2）画出系统的三种形式的信号流图。答案Y()ss+2s+3H()s===322F()ss+5s+8s+4(s+1s)(+1)解（1）（2）直接形式的信号流图如图题6.13（a）所示。1s+31H()s=××（3）s+1s+2s+2khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com级联形式的信号流图如图题6.13（b）所示。（4）()2−1−221⎛−1⎞Hs=++=+⎜−2⎟2s+1(s+2)s+2s+1s+2⎝s+2⎠并联形式的信号流图如图题6.13（c）所示。11s-1-1-11sskhaw.comF(s)-5Y(s)-8-4(a)11s-11s-11s-11F(s)Y()s-1-2-2(b)s-1211Y(s)1-1-2F(s)-11-1-1ss1-2-2(c)6.14已知系统的信号流图如图题6.14（a）所示。Y()sH()s=F()sh(t)（1）求系统函数及单位冲激响应；（2）写出系统的微分方程；khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comH(s)（3）画出与相对应的一种等效电路，并求出电路元件的值11s-1s-131F(s)Y(s)-4-3khaw.com(a)答案Y()ss+3s+31H()s====()2()()解（1）Fss+4s+3s+1s+3s+1故得系统的单位冲激响应为−th(t)=eU(t)（2）系统的微分方程为//()/()()/()()yt+4yt+3yt=ft+3ftH(s)注意，写系统的微分方程时，分子与分母中的公因式不能约去。331+1+ssH(s)==33s+4+s+3+1+（3）ss根据上式即可画出与之对应的一种等效电路，如图题6.14（b）所示，与之相对应的时域电路则如图题6.14（c）所示。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com11s-1s-131F(s)Y(s)-4-3(a)s3Ω++1Ωkhaw.comF()sY()s3--s(b)3Ω1H++1Ωf()ty()t1-F-3(c)图解6-14()()()−sht=Ut,Hs=e,6.15图题6.15（a）所示系统，其中13大系h(t)=(2−tU)(t−1)统的。求子系统的单位h()t冲激响应2。解图题6.15（a）系统的s域系统如图6.15（b）所示。故大系统的系统函数为khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com()[()][()(])1−s1−sHs=Lht=L−t−1−1Ut−1=−e+e2ss又题图6.15（b）得H(s)=[H()s−Hs]()H()s1231−s1−s1−s()−s−e+e=e−Hse22即ssskhaw.com1H(s)=22故sh()t=tUt()故得26.16系统的信号流图如图题6.16（a）所示。试用梅森公式求Y()sH()s=系统函数F()s。ht)(1+ft)(ΣH3t)(yt)(-ht)(2(a)答案解（1）求∆∑Li①求i:该信号流图共有3个环路，其传输函数分别为−1−1−1L=−s,L=−2s,L=−2s12khdaw.com3若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com故−1−1−1−1L=L+L+L=−s−2s−2s=−5s∑i123i∑LLmn②求m,n：该信号流图中两两互不接触的环路共有3组：−2−2−2LL=2s,LL=4s,LL=2s122331−2−2−2−2∑LL=2s+4s+2s=8smnkhaw.com故m,n∑LLLpqr③求p,q,r：该信号流图中三个互相不接触的环路只有1组L1，L2与L3，故−3∑LLL=LLL=−4spqr123p,q,r∑Pk∆（2）求kkP①求k：该信号流图共有4条前向通路，其传输函数分别为−1−1P=1×1×s×3×1×1=3s1−1−1P=1×1×s×2×1=2s2−1()−1P=1×1×s×1×−2×1=−2s3−1−1P=1×1×s×(−1)×1=−s4②求∆k：除去P1前向通路中所包含的支路和节点后，所剩子图如图题6.16（b）所示。根据该图可求得−1−2−2∆1=∆=1+5s+8s+4skhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comP除去2前向通路所包含的支路和节点后，所剩子图如图题6.16（d）所示。根据该图可求得−1∆4=1+sH()s（3）求42113s+16s+27H()s=∑P∆=[p∆+p∆+p∆+p∆]=KK1122334443khaw.com∆k∆s+5s+8s此题也可从信号流图直接求得，即42321⎛−1⎞3s+16s+27s+12H()s=++⎜−2+⎟=432ss+1(s+2⎝)s+2⎠s+5s+8s+4s-1s3111s-112F(s)Y(s)-11-1-1-1-2-1sss1-1-2-2()a()b-2-1-1ss-1s1-2-2-2()c()d()e−t6.17已知系统为单位冲激响应h()t=2eUt。求()khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comH()s（1）系统函数；f()t=cosUt()y(t)（2）若激励，求系统的正弦稳态响应答案2H()s=解（1）s+1khaw.com（2）由于系统的稳定系统，故2H(jω=)Hs()=s=jωjw+1()2°Hj1==2∠−45即j1+2故得系统的正弦稳态响应为()(°())yt=2cost−45Ut13H(s)=(()2)s+1s+4s+56.18已知系统函数，求激励f(t)=10cos2tU(t)时的正弦稳态响应y(t)。答案解(1)用解析法求H(s)因的极点全部位于s平面的作半开平面,系统为稳定的系统,故系统的频率特性为H(jω=)H(s)s=jωkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com即13131313−j1463.°H(j2)=====.072e(j2+1−)(4+j8+5(j2)+11)(+j8)5ej63.430°×65ej82.87°513ej1463.°故得正弦稳态响应为y()t=10×.072cos(2t−1463.°=)2.7cos2t−146(3.°Ut)()(2)用图解法解khaw.com13H(s)=([)(2)]s+1s+2+1故H(s)的极点为p1=−,1p2=−2+j,1p3=−2−j,H(s)的零﹑极点图如图题6.18所示.由图可求得22M=2+1=,5ψ=arctan=63.43°11121M=1+2=,5ψ=arctan=26.57°222223M=2+3=13,ψ=arctan=563.°33213−j146.3°H(j2=)=.072ej(ψ+ψ+ψ)MMMe123故123故得()ty=10×0.72cos(2t−146.3°=7.)2cos2t−146.(3°Ut)()可见两种求解方法所得结果全同.khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comjωM2ψ2×j1MM31ψ×1−2−1Oσψ3×−j1khaw.com图题6.186.19系统的零、极点分布如图题6.9所示。(1)试判断系统的稳定性；()−4Hjω=10(2)若jω，求系统函数H(s)；(3)画出直接形式的信号流图；(4)定性画出系统的模频特性|H(jω)|；(5)求系统的单位阶跃响应g(t)。jωH(jω)×j100−1Oσ10−4−j100O10−2×ω(rad•s−1)()a()ckhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com答案jω解(1)由于在轴上有一对共轭极点,故为临界稳定系统.s+1H()s=H0()()s+j100s−j100(2)()1−4Hj0=H=100()khaw.com故有j100×−j100H=1故0s+1s+1H()s==2222故得s+100s+0s+100(3)直接形式的信号流图如图题6.19(b)所示.jω+1H(jω)=H()s=s=jω(2)4jω+10(4)21+ωH(jω)=42故10−ω其模频特性如图6.19(c)所示.1F()s=(5)s,故−4−4−4−42s+110−10s+110−10s−210Y()s=Hs()()Fs==+=++1024242424s(s+10s)s+10ss+10s+10故得系统的单位阶跃响应为khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com()(−4−4−2)()gt=10−10cos100t+10sin100tUt11s-11-11s1F(s)Y()s−410khaw.com(b)图题6.196.20系统的信号流图如图题6.20所示.Y()sH()s=F()s(1)求系统函数；(2)欲使系统为稳定系统，求K的取值范围；(3)若系统为临界稳定，求H(s)在jω轴上的极点的值。-111-111s-1s-11sF(s)10-k-1图题6.20答案解(1)利用梅森公式可求得Ys()10s+10Hs()==32Fs()s+s+(10K+10s+)10khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com(2)罗斯阵列为3s110k+102s1101s10K00khaw.coms10可见,只要K＞0,系统即可稳定.(2)当K=0时,系统的特征方程为32s+s+10s=0H()s故得的极点为p=−,1p=j10rads,p=−j10radsjω123.即在轴上有两个极点,系统为临界稳定.khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com第七章习题7.1已知频谱包含有直流分量至1000Hz分量的连续时间信号f(t)延续1min，现对f(t)进行均匀抽样以构成离散信号。求满足抽样定理的理想抽样的抽样点数。答案khaw.comf=1000Hz解答：今m，故抽样频率应为：f≥2fsm3f=2f=2×10Hz最低抽样频率为sm。而最大的抽样间隔为11−4T===5×10ss3f2×10s故得最少抽样点数为t604N===12×10−4T5×10S个7.2已知序列f(k)={−2,−127,,,14,23,⋅⋅⋅}↑k=0试将其表示成解析（闭合）形式，单位序列组合形式，图形形式和表格形式。答案解答：（1）解析形式khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com2f(k)=(k−2)U(k)或2f(k)=k−2,k≥0（2）单位序列组合形式khaw.comf(k)=−2δ(k)−δ(k−1)+2δ(k−2)+7δ(k−3)+14δ(k−4)+23δ(k−5)+...（3）图形形式如图题7.2所示。f(k)23147...21k2345-2-17.2（4）表格形式如下：k0123456…f(k)-2-127142334…7.3判断以下序列是否为周期序列，若是，则其周期N为何值？3ππ(1)f(k)=Acos(k−)k∈Z78kj(−π)(2)f(k)=e8k∈Zkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com(3)f(k)=AcosωkU(k)0答案解答：若存在一个整数N，能使f(k+N)=f(k)f(k)则khaw.com即为周期为N的周期序列；若不存在一个周期N，则f(k)即为非周期序列。3ππ3π3ππ(1)f(k+N)=Acos[(k+N)−]=Acos[k+N−]78778取3πN=2nπ,n=2,1,0,...7故得2n×7N=3f(k)可见当取n=3时，即有N=14。故为一周期序列，其周期为N=14。k+NkNj(−−π)j(−π)j(2)f(k)=e8=e8e8f(k)N欲使为周期序列，则必须满足=2nπ，即N=16nπ，但由于n为整数，8π不是整数，故N不可能是整数，因此f(k)不可能是周期序列。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com（3）因f(k)=AcosωkU(k)为因果序列。故为非周期序列。也可以理解为是在02πk=0时刻作用于系统的周期序列，其周期为N=。ω07.4求以下序列的差分。22(1)y(k)=k−2k+3,求∆y(k);khaw.comk(2)y(k)=∑f(i),求∆y(k);i=0)3(y(k)=U(k),求∆[y(k−1)],∆y(k−),1∇[y(k−1)],∇y(k−).1答案解答：（1）方法一22∆y(k)=y(k+)1−y(k)=(k+1)−2(k+1)+3−[k−2k+3]=2k−12∆y(k)=∆y(k+1)−∆y(k)=2(k+1)−1−[2k−1]=2方法二2∆(y)k=∆[∆y(k)]=∆[y(k+)1−y(k)]=∆y(k+1)−∆y(k)=y(k+2)−y(k+1)−[y(k+)1−y(k)]=y(k+2)−2y(k+1)+y(k)=222(k+2)−2(k+2)+3−2[(k+1)−2(k+1)+3]+[k−2k+3]=2k(2)(y)k=∑f(i)=f(0)+f(1)+f(2)+...+f(k)i=0k+1y(k+)1=∑f(i)=f(0)+f(1)+f(2)+...+f(k)+f(k+1)i=0khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com故∆y(k)=y(k+)1−y(k)=f(k+)1(3)∆[y(k−)]1=y(k)−y(k−)1=U(k)−U(k−1)=δ(k)。这是先延迟后求差分。khaw.com因有∆y(k)=y(k+1)−y(k)故有∆y(k−1)=y(k)−y(k−)1=U(k)−U(k−1)=δ(k)这是先求差分后延迟。可见先延迟后求差分和先求差分后延迟是是一样的。∇[y(k−1)]=y(k−1)−y(k−2)=U(k−1)−U(k−2)=δ(k−1)（这是先求差分后延迟）∇y(k−)1=y(k−)1−y(k−)2=U(k−)1−U(k−)2=δ(k−)1（这是先求差分后延迟)7.5欲使图题7.5(a)与图题7.5(b)所示系统等效，求图题7.5(a)中的加权系数h(k)。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comf(k)DDDDh(0)h(1)h(2)h(k)Σy(k)(a)1y(k)khaw.comf(k)D∑DD5-6(b)7.5答案解答：两个系统等效，意即它们的单位响应相等。图题(b)的差分方程为y(k)−5y(k−1)+6y(k−2)=f(k)+f(k−1)故得转移算子2E+EE−1⎡12⎤H(E)==1+6=1+6+2⎢⎥E+5E+6(E−2)(E−3)⎣E−2E−3⎦故得k−1k−1h(k)=δ(k)+6[−1(2)U(k−1)+2(3)U(k−1)]⎡k1k1⎤=δ(k)+6−1(2)U(k−1)+2(3)U(k−1)⎢⎥⎣23⎦kk=δ(k)−3(2)U(k−1)+4(3)U(k−1)因为当k=0时有khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comh(0)=1−0+0=1故上式可写为[kk]h(k)=−3(2)+4(3)U(k)因由此式也可得到khaw.comh(0)=−3+4=1图题(a)的差分方程为∞y(k)=h(0)f(k)+h(1)f(k−1)+...(+)hi(fk)−i=∑(h)i(fk−)i=k(k)∗f(k)i=0欲使图题(b)和(a)两个系统等效，图题(a)的单位响应也应为[kk]h(k)=−3(2)+4(3)U(k)f(k)f(k)7.6已知序列1和2的图形如图题7.6所示。求y(k)=f(k)∗f(k)12f1(k)f2(k)2211111516kk-5-4-3-201234-5-4-3-201234(a)(b)7.6答案khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com(yk)=f(k)∗f(k)12=[δ(k+1)+2δ(k)+δ(k−1)]∗[δ(k+2)+δ(k+1)+2δ(k)+δ(k−1)+δ(k−2)]=δ(k+3)+3δ(k+2)+5δ(k+1)+6δ(k)+5δ(k−1)+3δ(k−2)+δ(k−3)7.7求下列各卷积和。k(1)U(k)∗U(k)(2)(.025)U(k)∗U(k)kkkhaw.com(3)(5)U(k)∗(3)U(k)(4)kU(k)∗δ(k−2))答案解答：(1)U(k)∗U(k)=(k+1)U(k)k+1k1−(.025)4k+1(2)(.025)U(k)∗U(k)=U(k)=[1−(.025)]U(k)1−.0253k+1k+1kk(5)+(3)1k+1k+1(3)(5)U(k)∗(3)U(k)=U(k)=[(5)+(3)]U(k)5−32)4(kU(k)∗δ(k−)2=U(k)+U(k−)1+U(k−)2y(k)7.8求下列各差分方程所描述的离散系统的零输入响应。(1)y(k+2)+2y(k+1)+y(k)=,0y(0)=,1y(1)=0;(2)y(k)−7y(k−1)+16y(k−2)−12y(k−3)=,0y(1)=−,1y(2)=−,3y(3)=−5。答案解答：（1）对差分方程进行移序变换得khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com2(E+2E+1)y(k)=0特征方程为2E+2E+1=0得特征根为p=p=−112故零输入响应的通解为khaw.comky(k)=(A1+A2k)(−1)U(k)故有y)0(=A=1y)1(=A+A=01，12故得A=1,A=−112故得零输入响应为ky(k)=(1−k)(−1)U(k)（2）对差分方程进行移序变换得−1−2−332(1−7E+16E−12E)y(k)=0(E−7E+16E−12)y(k)=0即特征方程为32E−7E+16E−12=0特征根为khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comp=p=,2p=3123故零输入响应的通解为kky(k)=[(A+Ak)2+A(3)]U(k)123故有y()1=(A+A)2+3A=−1123khaw.com22y(2)=(A+A)2+A×3=−312333y(3)=(A+A2)+A×3=−5123联解得A=−,1A=−,1A=1123故得零输入响应为kky(k)=[(−1−k)2+3]U(k)7.9已知系统的差分方程为51y(k)−y(k−1)+y(k−2)=f(k)−f(k−2)66h(k)求系统的单位响应。答案解答：系统差分方程的转移算子为khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com−221−EE−1H(E)===5−11−22511−E+EE−E+66662E1−=1111(E−)(E−)(E−)(E−)2323⎡⎤⎡⎤⎢E⎥−1⎢E⎥E⎢⎥−E⎢⎥=1111⎢(E−)(E−)⎥⎢(E−)(E−)⎥⎣23⎦⎣23⎦⎡⎤⎡⎤⎢32⎥−1⎢32⎥khaw.comE⎢−⎥−E⎢−⎥=1111⎢E−E−⎥⎢E−E−⎥⎣23⎦⎣23⎦⎡⎤EE−1⎢32⎥3−2−E⎢−⎥1111E−E−⎢E−E−⎥23⎣23⎦故得⎡1k1k⎤⎡1k−21k−2⎤h(k)=3()−2()U(k)−3()−2()U(k−2)⎢⎥⎢⎥⎣23⎦⎣23⎦7.10已知差分方程y(k+2)−5y(k+1)+6y(k)=U(k)系统的初始条件y(0)=1,y(1)=5xxy(k)求全响应。答案y(k)解答：（1）求零输入响应xkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com2E−5E+6=0得特征根为p=,2p=312故kky(k)=A(2)+A(3)x12khaw.comyx(0)=A1+A2=1y(1)=2A+3A=5x12联解得A=−,2A=312故y(k)=[−2(2)k+3(3)]kU(k)=[−(2)k+1+(3)k+1]U(k)xh(k)（2）求1−11H(E)==+2E−5E+6E−2E−3故得k−1k−1h(k)=−(2+3)U(k−1)y(k)（3）求零状态响应fk−1k−1y()k=h(k)∗f(k)=[−2U(k−1)+3U(k−1)]∗U(k)=fk−1k−1−2U(k−1)∗U(k)+3U(k−1)∗U(k)khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com查卷积和表得11kky(k)=[−(2)+(3)]U(k)f22全响应为⎡1k7k⎤(y)k=y(k)+y(k)=−3(2)+(3)U(k)xf⎢22⎥⎣⎦7.11khaw.com某人每年初在银行存款一次，第1年存款1万元，以后每年初将上年所得利息和本金以及新增1万元存入当年，年利息为5%。(1)列此存款的差分方程；(2)求第10年底在银行存款的总数。答案y(k)解答：（1）设第k年初银行存款总额为，则差分方程为5y(k+)1−y(k)=y(k)×+U(k)100y(k+1)k+1U(k)k+1式中为年初存款的总数，为第年初新增存款1万元。整理之得y(k+1)−.105y(k)=U(k)y(0)=0由于，故只存在零状态响应。传输算子为1H(E)=E−.105故k−1k(k)=(1.05)U(k−1)故khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comk−1(y)k=U()k∗h(k)=U(k)∗(.105)U(K−1)=K1−(.105)Ku(K−1)=20[(.105)−1]u(K−1)1−.105当k=10时有10y(10)=20[(1.05)−1]×1=12.5779万元故第10年底银行的存款总数为khaw.comy(10)×⎡⎢⎣1+1005⎤⎥⎦=13.2068万元7.12已知差分方程为y(k)+3y(k−1)+2y(k−2)=f(k)激励kf(k)=2U(k)初始值y(0)=,0y(1)=2y(k)试用零输入-零状态法求全响应。答案y(k)解答：（1）求零输入响应x。系统的特征方程为2E+3E+2=0khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com得特征根为p=−1,p=−212y(k)故得零输入响应x的通解为kky(k)=A(−1)+A(−2)x12A,A待定系数12必须根据系统的初始状态来求，而不能根据全响应的初始值ykhaw.com)0(=0,y)1(=2来求。又因为激励f(k)是在k=0时刻作用于系统的，故初始状y(−),1y(−2)y(−),1y(−2)态应为。下面求。取k=1，代入原差分方程有y(1)+3y(0)+2y(−1)=2即2+0+2y(−1)=2故得y(−1)=0取k=0，代入原差分方程有y(0)+3y(−1)+2y(−2)=1即0+0+2y(−)2=1故得khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com1y(−2)=21y(−2)=y(−1)=02将所求得的初始状态，代入式（1）有1y(−1)=−A−A=0x12211y(−2)=A+A=x12khaw.com42A=,1A=−2联解得12。故得零输入响应为kky(k)=(−1)−2(−2),k≥0x（2）差分方程的转移算子为21EH(E)===−1−221+3E+2EE+3E+2E⎛−12⎞E=E⎜+⎟=(E+1)(E+2)⎝E+1E+2⎠−E2E+E+1E+2[kk]h(k)=−(−)1+(2−)2U(k)故得单位响应为（3）零状态响应为kkky(k)=h(k)∗f(k)=2∗[−(−1)+2(−2)]=fkkkk2∗[−(−1)+2]∗2(−2)=1k1kk−(−1)+(2)+(−2),k≥033(y)k=y(k)+y(k)（4）全响应xf，即khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comkk1kk1k2kk1k=y(k−)(−1)−2(2−)−(1)+−(2)+(2)=−(1)−(−2)+(2),k≥03333零输入响应零状态响应强迫响应自由响应7.13已知离散系统的差分方程与初始状态为51y(k+2)−y(k+1)+y(k)=f(+1k)−2f(k),y(0)=y(1)=,1f(k)=U(k)khaw.com66(1)求零输入响应yx(k)，零状态响应yf(k)，全响应y(k)；(2)判断该系统是否稳定；(3)画出该系统的一种时域模拟图。答案解答：（1）E−2−910H(E)==+25111E−E+E−E−6623故零输入响应的通解为⎡1k1k⎤y(k)=A()+A()U(k)x⎢1223⎥⎣⎦故有y(0)=A+A=112khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com11y(1)=A+A=11223A=,4A=−3联解得12。故得零输入响应为⎡1k1k⎤y(k)=4()+3()U(k)x⎢23⎥⎣⎦（2）系统的单位序列响应为khaw.comh(k)=⎡⎢⎣−9(12)k−1+10(13)k−1⎤⎥⎦U(k−1)故零状态响应为⎡1k−11k−1⎤y()k=(hk)∗f(k)=U(k)∗−9()+10()U(k−1)=f⎢23⎥⎣⎦⎧⎡1k⎤⎡1k⎤⎫⎨−18⎢1−()⎥+15⎢1−()⎥⎬U(k−1)=⎩⎣2⎦⎣3⎦⎭⎡1k1k⎤18()−15()−3U(k)⎢⎥⎣23⎦（3）全响应为⎡1k1k⎤(y)k=y(k)+y(k)=22()−18()−3U(k)xf⎢⎥⎣23⎦11,（4）由于差分方程的特征根23的绝对值均小于1，故系统是稳定的（5）系统的一种时域模拟图如图题7.13所示khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com1f(k)∑DD-2∑y(k)5/6-1/67.137.14已知系统的单位阶跃响应11k4kkhaw.comg(k)=[−(−1)+(−2)]U(k)623求系统在kf(k)=(−3)U(k)y(k)激励下的零状态响应f，写出该系统的差分方程，画出一种时域模拟图。答案h(k)解答：先求单位响应。因有(δ)k=∇U(k)=U(k)−U(k−1)故根据系统的差分性有(h)k=∇g(k)=g(k)−g(k−1)⎡11k4k⎤⎡11k−14k−1⎤=−(−1)+(−2)U(k)−−(−1)+(−2)U(k−1)⎢⎥⎢⎥⎣623⎦⎣623⎦[kk]=−(−1)+2(−2)U(k)故得khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comkkky()k=h(k)∗f(k)=(−3)U(k)∗[−(−1)+2(−2)]U(k)f⎡9kk1k⎤=(−3)−4(−2)+(−1)U(k)⎢⎥⎣22⎦h(k)又由的表达式可求得转移算子为2−E2EE1H(E)=+==2−1−2E+1E+2E+3E+21+3E+2E故得系统的差分方程为khaw.comy(k)+3y(k−1)+2y(k−2)=f(k)其模拟图如图题7.14所示y(k)f(k)∑DD-3-27.147.15已知零状态因果系统的单位阶跃响应为kkg(k)=[2+3(5)+10]U(k)(1)求系统的差分方程；(2)若激励f(k)=2G(k)=2[U(k)−U(k−10)]10y(k)求零状态响应。答案khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comg(k)解答：（1）由阶跃响应的表达式可知，特征方程有两个特征根：p=2,p=512故知该系统是二阶的。故可设系统的差分方程为my(k)+ay(k−1)+ay(k−)2=bf(k−i),(i=2,1,0,...,m)12∑ii=0系统的特征多项式为khaw.com22E+aE+a=(E−2)(E−5)=E−7E+1012故得a=−,7a=1012故得差分方程为my(k)−7y(k−1)+10y(k−2)=∑bif(k−i)i=0bh(k)f(k)=δ(k)下面再求系数。先求单位响应i。当激励时，系统的差分方程变为mh(k)−7h(k−1)+10h(k−2)=∑biδ(k−i)i=0因有(δ)k=∇U(k)=U(k)−U(k−1)故根据线性系统的差分性有khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com(h)k=∇g(k)=g(k)−g(k−1)kkk−1k−1=[2+3(5)+10]U(k)−10+([2)+3(5)]U(k−1)k−1k−1=14δ(k)+[(2)+12(5)]U(k−1)故得：h(−2)=,0h(−1)=,0h(0)=14,h(1)=13,h(2)=62,h(3)=304,h(4)=1508,...将这些值代入式（1）得khaw.com⎧14,k=0⎪⎪−85,k=1h(k)−7h(k−1)+10h(k−2)=⎨111,k=2⎪⎪⎩,0k≥3故得系数b=14,b=−85,b=111,b=b=...=b=001234m最后得差分方程为y(k)−7y(k−1)+10y(k−2)=14f(k)−85f(k−1)+111f(k−2)实际上，由于因果系统总是有m≤n，今n=2阶，故必有b=b=...=b=034m（2）根据线性系统的齐次性与移序不变性可得[]{[kk]k−10[k−10]}y(k)=2g(k)−g(k−10)=22+3(5)+10U(k)−2+3(5)+10U)k−107.16图题7.16所示(a)，(b)，(c)三个系统，已知各子系统的单位响应为h(k)=U(k)1h(k)=δ(k−3)2khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comkh(k)=(0.8)U(k)3试证明三个系统是等效的，即h()k=h(k)=h(k)abc。y1(k)h2(k)δ(k)h1(k)−y3(k)∑h3(k)ha(k)khaw.com+y2(k)(a)y1(k)h2(k)δ(k)h1(k)h3(k)−∑h(k)b+y2(k)(b)h2(k)h1(k)y1(k)−δ(k)h3(k)∑hc(k)+y2(k)h1(k)(c)7.16答案解答：欲证明三个系统相互等效，只要证明三个系统的单位响应相同即可。h(k)（1）求图题7.16(a)的单位响应akhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comy(k)=δ(k)∗h(k)∗h(k)=δ(k)∗U(k)∗δ(k−)3=U(k−)3112y(k)=δ(k)∗h(k)=δ(k)∗U(k)=U(k)21y(k)=y(k)−y(k)=U(k)−U(k−)3321h(ak)=y3(k)∗h3(k)[]kkk=U(k)−U(k−3)∗8.0U(k)∗8.0U(k)−U(k−3)∗8.0U(k)k+1k−2=5(1−8.0)U(k)−5(1−8.0)U(k−3)h(k)（2）求图题7.16(b)的单位响应bkhaw.com(y1)k=(δ)k∗h(1)k∗h3(k)∗h2(k)kk−2=δ(k)∗U(k)∗8.0U(k)∗δ(k−3)=5(1−8.0)U(k−3)kk+1(y)k=(δ)k∗h()k∗h()k=δ(k)∗U(k)∗8.0U(k)=5(1−8.0)U(k)213(h)k=y()k−y(k)=h(k)b21ah(k)（3）求图题7.16(c)的单位响应c(y)k=(δ)k∗h()k∗h(k)∗h(k)1321kk−2=δ(k)∗8.0U(k)∗δ(k−3)∗U(k)=5(1−8.0)U(k−3)kk+1(y)k=(δ)k∗h(k)∗h(k)=δ(k)∗8.0U(k)∗U(k)=5(1−8.0)U(k)231(h)k=(y)k−y()k=h(k)=h(k)c21ab故三个系统是等效的。7.17试写出图题7-17(a)，(b)所示系统的后向与前向差分方程。y(k)y(k)f(k)∑Df(k)∑DD-5-1/5-6(a)(b)7.17答案解：khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com（a）1y(k+1)+y(k)=f(k+1)51y(k)+y(k−1)=f(k)5（b）y(k+)2+5y(k+)1+6y(k)=f(k+)2khaw.comy(k)+5y(k−1)+6y(k−2)=f(k)khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com第八章习题8.1求长度为N的斜坡序列⎧k,0≤k≤N−1Rk()=⎨N⎩0,k<0,k≥N的z变换khaw.comRN()z，并求N=4时的RN()z(见图题81)。N-1432101234N-1Nk答案解方法一设G()k=Uk()−Uk(−N),则NRk()=kGk()NN−N+1zzG()z=−N因z−1z−1故−N+1−N+2−N+1−N+1−N+1−N+2dzz+Nz−Nzz−z+Nz−NzR()z=−zG()z=−=NN222dz(z−1)(z−1)(z−1)当N=4时khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com−3−3−242z−z+4z−4zz+−34zz+2z+3Rz()===42323(z−1)zz(−1)z方法二R()k=δ(k−1)+2(δk−2)+3(δk−3)+⋯+(N−1)(δk−N+1)N(N−2)N−3N−4−1−2−3−(N−1)z+2z+3z+⋯+(N−1)R()z=z+2z+3z+⋯+(N−1)z=N(N−1)zkhaw.com2z+2z+3当N=4时Rz()=43zFz()Fz()8.2求下列序列的z变换，并标明收敛域，指出的零点和极点。1k()Uk()(1)21k()U(−k)(2)21k2k()Uk()()−Uk()(3)431k−()U(−−k1)(4)21k1k()Uk()()−U(−−k1)(5)53ejkω0Uk()(6)答案khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com解z1（）1()Fz=,z>12z−21极点P=,零点z=0。112∞+∞−1+∞1k−kzk1k11（）2()Fz=∑()z=∑()=∑()=,z12123z−z−12(z−)(z−)434312极点P=,P=;零点z=0。12143−∞−∞−11k−kzk(4)()Fz=−∑()z=−∑()+1k=−12k=0212z11=+=,z<2z−12z−121极点P=,零点z=0.112z1(5)()Fz=,z>115z−53z1()Fz=,z<23z−13z3z11故()Fz=Fz()−Fz()=−,1jωze−0极点P=ejω0.khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comFz()8.3试用z变换的性质求下列序列的z变换。1kfk()=[1(1)]()−−Uk(1)2fk()=Uk()−Uk(−6)(2)kkhaw.com(3)fk()=k(1)−Uk()()fk=kk(+1)()Uk(4)πfk()=coskUk()(5)21kπfk()=()cos(kUk)()(6)22答案解1z1zzFz()=×−×=2(1)2z−12z+1z−1−5zz−6z−zFz()=−z=(2)z−1z−1z−1dz−zFz()=−z[]=2dzz+1(z+1)(3)khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com(4)fk()=×kkUk()+kUk()dzz故Fz()=−z[]+22dz(z−1)(z−1)2zz(+1)zz=+=323(z−1)(z−1)(z−1)ππ1jk−jkfk()=[e2+e2]()Uk(5)2khaw.com21zzzFz()=[+]=ππ22jjz+1z−e2z+e2故(6)由尺度变换性质得z124z2Fz()==2z24z+1()+112Fz()fk()8.4求下列各的反变换。2z+z(1)()Fz=,z>1;2(z−1)(z−+z1)z(2)()Fz=,||1;z>2(z−1)(z−1)−5z(3)()Fz=,||2z>z+2答案解khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com(1)z+12−1−1Fz()=z[]=z[++]11313z−11313(z−1)(z−−j)(z−+j)z−−jz−+j222222222zzz=−[+]ππz−1j−jz−e3z−e3故得ππjk−jkππ33jk−jke+efk()=2()[Uk−e3+e3]()Uk=2()Uk−22khaw.comπ=2[1cos−kUk]()3111zz−zz424Fz()==++22(z+1)(z−1)z+1(z−1)z−1(2)故1k1k1kfk()=[(1)−+k(1)−(1)]()Uk4241k=[(1)−+2k−1]()Uk4−6z(3)()Fz=zz+2k−6故fk()=−(2)Uk(−6)fk()Fz()f(0)f(1)f()∞8.5已知序列的如下，求初值,及终值。2z++z1(1)()Fz=,z>11(z−1)(z+)22z(2)()Fz=,z>2(z−2)(z−1)答案khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com解2z++z1(1)(0)f=lim=1z→∞1(z−1)(z+)233z(z+)223f(1)=lim[()zFz−f(0)]=lim=z→∞z→∞12(z−1)(z+)2khaw.comz2++z1f()∞=lim(z−1)()Fz=lim=2z→1z→11z+22z(2)(0)f=lim=1z→∞(z−2)(z−1)zz(3−2)f(1)=lim[()zFz−f(0)]=lim=3z→∞z→∞(z−2)(z−1)因为Fz()的收敛域z>2，不满足应用终值定理的条件，故终值不存在。8.6已知离散系统的差分方程为yk()−yk(−1)2(−yk−2)=fk()2(+fk−2)1y(2)−=−系统的初始状态为y(1)2−=,2；激励fk()=Uk()。求系统的零输入响应ykx()，零状态响应yf()k，全响应yk()。答案解将差分方程进行z变换得khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com−1−1−1−1−k−2−2−k−2Yz()[−zYz()+z∑ykz()]2[−zYz()+z∑ykz()]=Fz()+2zFz()k=−1k=−2−1−2−1−2(1−z−2z)()Yz=(12+z)(1)y−+2(2)y−+(12+z)()Fz即−1−2(12+z)(1)y−+2(2)y−12+z()Yz=+Fz()−1−2−1−2�����������1−z−2z1���������−z−2z故得零输入响应Yx()z零状态响应Yf()zkhaw.com即Yz()=(12+z−1)(1)y−+2(2)y−=(12+z−1)22(×+−12)=z2+4zx−1−2−1−221−z−2z1−z−2zz−−z2z+42−12zz=z[]=z[+]=−(z−2)(z+1)z−2z+1z−2z+1故得零输入响应为kkyk()=2(2)−−(1),k≥−2xkkyk()=[2(2)−−(1)](Uk+2)或x13−2−12+zz2222z1z3zYz()=×=z[++]=+−f−1−21−z−2zz−1z−2z+1z−1z−22z+12z−1故得零状态响应为k1k3kyk()=[2(2)+(1)−−(1)]()Ukf22故又得全响应为kkk1k3kyk()=yk()+yk()=[2(2)−−(1)](Uk+2)[2(2)++(1)−−(1)]()Ukxf22Hz()8.7根据下面描述离散系统的不同形式，求出对应系统的系统函数。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com(1)()yk−2(yk−1)5(−yk−2)+6(yk−3)=fk()32−E(2)()HE=3121E−E+E218(3)单位响应hk()如图题8.7(a)所示.。(4)khaw.com信号流图如图题8.7(b)所示.22311121k4-10234(a)(b)5图题8.7答案解(1)在零状态下对差分方程进行z变换为−1−2−3(1−2z−5z+6z)()Yz=Fz()3Yz()zHz()==32Fz()z−2z−5z+6故32−zHz()=HE()=Ez=1132z−z+z(2)218hk()=δ()k+δ(k−1)+2(δk−2)+2(δk−3)(3)因khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com32−1−2−3z+z+2z+2Hz()=+1z+2z+2z=3故zhk()=Uk()+Uk(−2)2(−Uk−4)或−1−32zz2z3z+2zHz()=+−=2故z−1z−1z−1z−4z−5(4)根据梅森公式khaw.com−1232+z3z+2zHz()==−1−2214−z−5zz−4z−543k2kgk()[=−(0.5)+(0.2)]()−Uk8.8已知离散系统的单位阶跃响应3721。若需获10kkyk()=[(0.5)−−(0.2)]()Uk得的零状态响应为7。求输入fk()。答案解24z3z2zzz(−0.2)Gz()=Zgk[()]=−+=3z−17z−0.521z+0.2(z−1)(z−0.5)(z+0.2)z又因Gz()=HzFz()()=Hz(),故得系统函数为z−1z−1zz(−0.2)Hz()=Gz()=z(z−0.5)(z+0.2)又零状态响应的z变换为khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com10zzzYz()=[−]=7z−0.5z+0.2(z−0.5)(z+0.2)又Yz()=HzFz()()Yz()1故Fz()==Hz()z−0.2k−1khaw.com故得激励fk()=(0.2)Uk(−1)fk()=kUk()8.9离散时间系统，当激励时，其零状态响应1kyk()=2[()−1]()Ukfhk()2。求系统的一种z域模拟图和单位响应。答案dzzFz()=−z()=2dzz−1(z−1)解2z2z−zYz()=−=f1z−11z−(z−)(z−1)22由Y()z=HzFz()()可得fYzf()1−zHz()==Fz()1z−2由该系统的z域模拟图如图题8.9所示。单位响应为1k−11khk()=()Uk(−1)()−Uk()22khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com-1111/2图题8.98.10已知图题8.10(a)所示系统。(1)写出系统的差分方程；(2)求系统函数Yz()Hzkhaw.com()=Fz()，画出零极点图；(3)求单位响应hk()，并画出波形；(4)若保持其频率特性不变，试再画出一种时域模拟图。jImzDDRe[z]-0.5D(a)(b)DD111/215678-0.5-1012349k-1/4-1/4(c)(d)答案解(1)yk()=fk(−1)+yk(−1)0.5(−yk−2),故系统的差分方程为yk()−yk(−1)0.5(+yk−2)=fk(−1)−1zz(2)()Hz==−1−221−z+0.5zz−+z0.5khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com11故得系统函数Hz()的零点为z=0,极点为p=±j.零极图如图题8.10(b)所示.11,222zjzjzHz()==−20.51111z−+zz−+jz−−j(3)因222211k11k2kπhk()=j[(−j)−(+j)]()Uk=2()sinkUk()故222224hkkhaw.com()的波形如图题8.10(c)所示.Hz()(4)根据和题目的要求，可画出另一种时域模拟图，如图8.10(d)所示，可见比原模拟图节省一个延迟器。1yk()−yk(−1)=fk()8.11已知离散系统的差分方程为3。(1)画出系统的一种信号流图；1k1kyk()=3[()−()]()Ukffk()(2)若系统的零状态响应为23，求输入。答案1(1)()Hz=,故得系统的信号流图如图题8.11所示.1−11−z33z3zzYz()=−=f1111z−z−2(z−)(z−)2323Yz()1fFz()==Hz()12(z−)2khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com11k−1故fk()=()Uk(−1)22111113/41/3-1/8khaw.comYz()Hz()=Fz()8.12已知离散系统的信号流图如图题8.12所示。(1)求及单位序列hk()gk()响应；(2)写出系统的差分方程；(3)求系统的单位阶跃响应。答案2z2z−z(1)()Hz==+231111k1kz−z+z−z−故hk()=[2()−()]()Uk48242431(2)(yk+2)−yk(+1)+yk()=fk(+2)4831z或yk()−yk(−1)+yk(−2)=fk()(3)()fk=UkFz(),()=48z−1182zzzz−2z33Gz()=HzFz()()==++1111z−1(z−)(z−)(z−1)z−z−24241k11k8k故得gk()=−[2()+()+(1)]()Uk2343z1Hz()=Hz()=hk()=Uk()238.13图题8.13所示系统，1,z+1,z,fk()=Uk()−Uk(−2)yk()。求零状态响应。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com+-答案zHz()=。大系统的系统函数1解z−1khaw.comzz12Hz()=[Hz()−HzHz()]()=[−]=123z−1z+1z(z−1)(z+1)zz−2z+1Fz()=−z=z−1z−1z22z−2Yz()=HzFz()()==z(z−1)zz−1k故得yk()=2(1)Uk(−2)=2(Uk−2)8.14已知离散系统的系统函数为323z−5z+10zHz()=32z−3z+7z−5试画出级联形式的模拟图与并联形式的信号流图。答案223z−5z+102zz(1)()Hz=z=+322解z−3z+7z−5z−1z−2z+5其级联形式的时域模拟图如图题8.14(a)所示，并联形式的信号流图如图题8.14(b)所示。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com3-5∑DD10∑y(k)D2--55(a)2-1z1khaw.comf(k)1111y(k)-1-11zz2--55(b)图题8.141k1kyk()=3[()−()]()Uk8.15已知图题8.15所示系统的零状态响应为23。Hz()(1)求，画出零极点图；(2)求频率特性，大致画出幅频特性曲线(T=1)。1111/31/3(a)(b)1.53/40(c)khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com答案解1z(1)()Hz==1−111−zz−331故得零点z=0，极p=。故零、极点图如图题8.15(b)所示。113jTω1(2)(He)=Hz()=khaw.comze=jTω1−jω1−e3jTω1故幅频特性He()=，其曲线如图题8.15(c)所示。102−cosω938.16已知图题8.16所示离散系统。(1)写出系统的差分方程；πfk()=Uk()[cos(+k)cos+πkUk]()(2)若3，求系统的稳态响应yk()-0.80.8D。答案解(1)由模拟图得yk()=fk()0.8()−fk+0.8(yk−1)khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com故系统得差分方程为()0.8(yk−yk−1)=0.2()fk0.2z(2)()Hz=,z>0.8且T=1,故z−0.8jωjω0.2e0.2cosω+j0.2sinωHe()=Hz()==ze=jωjωe−0.8cosω−0.8+jsinωj0�当khaw.comω=0时，He()=1，（）ϕ0=0ππjπ�当ω=时，He(3)=0.22，（）ϕ=−49.133jπ�当ω=π时，He()=0.11，（）ϕπ=0π今fk()=+1cos(k)+cosπk,故系统的稳态响应为3π�()yk=+10.22cos(k−49.1)0.11cos+πk3khk()=0.5[()Uk+Uk(−1)]8.17已知离散系统的单位响应为。(1)写出系统的差分方程；(2)画出系统的一种时域模拟图；jkωfk()=e00.5,且取T=1,故khaw.comz−0.5−jωjω10.5+eHe()=−jω10.5−ejkωjω今激励fk()=e,根据He()意义，可知零状态响应为−jωjωjkω10.5+ejkωyk()=He()e=e−jω10.5−eπ(4)当ω=时2πj1−j0.5sin(π2)1−j0.5He(2)==1+j0.5sin(π2)1+j0.5π2j10.5+He(2)==1210.5+π�ϕ（）=−2arctan0.5=−53.132故得正弦系统的稳态相应为π��π�yk()=cos(k+45−53.13)=cos(k−8.13)22khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com8.18图题8.18所示为非递推型滤波器，抽样间隔T=0.001s。今为了提供直流π3ω=×103增益为1和在2与π×10rad/s两频率时的增益为零，试确定系数a,,,aaaHz()0123，并求此滤波器的系统函数及其模频特性。DDDkhaw.com答案yk()=afk()+afk(−1)+afk(−2)+afk(−3)解因0123−1−2−3故Hz()=a+az+az+az0123jTω−jTω−j2ωT−j3ωTHe()=a+ae+ae+ae0123当ωT=0时有a0+a1+a2+a3=1π当ωT=时有2a0−ja1−a2+ja3=0π当ωT=时有2a0−a1+a2−a3=01联解得a=a=a=a=0123432z+z++z1故Hz()=34zkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comjTω1−jTω−j2ωT−j3ωTHe()=(1+e+e+e)4jTω122He()=(1cos+ωT+cos2ωT+cos3ωT)+(sinωT+sin2ωT+sin3ωT)28.19已知一数字滤波器的差分方程为5(yk−2)=fk()+fk(−1)+fk(−2)+fk(−3)+fk(−4)khaw.com输入信号fk()为频率f=5Hz的正弦信号，信号的抽样频率fs=250Hz，同时fk()有频率为50Hz的干扰信号存在。试求此滤波器能否将输入信号基本上完全通过，而同时将干扰信号基本上完全滤除。答案解由差分方程可求得系统函数为−1−2−3−42341+z+z+z+z1++zz+z+zHz()==−225z5z因Hz()的极点p1=p2=0，故系统为稳定系统，故得系统的频率特性为−jTω−j2ωT−j3ωT−j4ωTjTω11+e+e+e+eHe()=Hz()ze=jTω=×−j2ωT5ea=1−jTω式中的分子首项1，公比q=e的等比级数前五项的和，故根据等比级数na(1−q)1S=n前n项求和的公式1−q可得−jTω5−5jTω1[1(−e)]1−e分子==−jTω−jTω1−e1−e再代入上式有khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com555−jωTjωT−jTω−j5ωT222jTω11−ej2ωT1e(e−e)j2ωTHe()=××e=××e−jTω11151−e5−jωTjωT−jωTe2(e2−e2)55jωT−jTωe2−e25sinωT1−j2ωT2jj2ωT12=×e×e=×51151jωT−jωTe2−e2sinωT22j11πωT=2πf=2π××5=f25025今已知khaw.coms。代入上式得5ππsin×sinjTω12251100.3090He()=×=×=0.2×=0.98411≈51π5π0.0628sin×sin22550fk()此结果表明，该滤波器基本上能将输入信号全部通过。f=50Hz对于频率的干扰信号有112πωT=2πf×=2π×50×=f2505s52πsin×jTω12510He()=×=×=0512π5πsin×sin故得255此结果表明，该滤波器能够将50Hz的干扰信号完全滤除。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comHz()8.20已知离散系统系统函数的零极点分布如图题8.20所示，lim()hk=4k→∞。(1)求系统函数Hz()；(2)若系统的零状态响应为kyk()[13(3)]()=+−Ukfk()，求激励。答案khaw.comz（）设1Hz()=H0解z−1z因有lim()hk=lim(z−1)()Hz=lim(z−1)H=H=400k→∞z→1z→1z−1z故得Hz()=4z−1zz(2)()Yz=+3=HzFz()()z−1z+3z3z+Yz()z−1z+3z故Fz()===Hz()4zz+3z−1k故得fk()=−(3)Uk()1lim()hk=8.21已知离散系统系统函数Hz()的零极点分布如图题8.21所示，k→∞3，系统的初始条件为y(0)=2,y(1)1=。(1)求Hz()及零输入响应ykx()；(2)若kykfk()=−(3)Uk()，求零状态响应f()。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com答案z（）设1Hz()=H01khaw.com(z+)(z−1)解2z21因有lim()hk=lim(z−1)()Hz=lim(z−1)H=H=00k→∞k→31z→1133(z+)(z−1)21故H=021z1z2故得Hz()=×=21211(z+)(z−1)z−z−2221(2)()Hz的极点为p=−,p=1。故有1221kk()yk=A(−)+A(1)x122代入初始条件有y(0)=A+A=2x121y(1)=−A+A=1x12224联解得A=,A=123321k4k故得yk()=[(−)+(1)]()Ukx323khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comz(3)()Fz=z+32z3z1z1z故Yz()=FzHz()()==−×+×+×f120z+315112z−12(z+3)(z−1)(z+)z+223k11k1k故得yk()=−[(3)−+(−)+(1)]()Ukf2015212khaw.comHz()8.22图题8.22所示离散系统。(1)求，并画出零极点图及收敛域；(2)hk()写出系统的差分方程；(3)求；(4)判断系统的稳定性；71k71k91k5yk()[()=−(−)−()+]()Ukf(5)已知系统的零状态响应为8212021036，求激fk()励。(a)0(b)khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com答案解31−211−111−1−z3(+z)(−z)Yz()4323231（）1Hz()===,z>Fz()1−11−21−31−11−11−131−z−z+z(1−z)(1+z)(1−z)341222311122故极点为p=，p=，p=−；零点为z=0，z=，z=−。12312323233零极点分布及收敛域如图题8.22(b)所示。khaw.com(2)系统的差分方程为11131yk()−yk(−1)−yk(−2)+yk(−3)=fk()−fk(−2)341243977−−5840(3)()Hz=++1−11−11−11−z1−z1+z32291k71k71k故hk()=[()−()−(−)]()Uk5382402(4)由于Hz()的极点均于单位圆内部，故该系统为稳定系统。71719151(5)()Yz=×−×−×+×81120110161−1−1−1−1−z1−z1+z1−z22311−111−13(+z)(−z)2323=1−11−11−1−1(1−z)(1+z)(1−z)(1−z)223Yz()1z故()Fz===−1Hz()1−zz−1故得fk()=Uk()khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com第九章习题x(t)x(t)9.1图题9.1所示电路，已知1与2为状态变量，试证明以下各对变量是否都可以作为状态变量。(1)i(t),u(y);(2)i(t),u(t);(3)u(t),u(t);(4)i(t),u(t);(5)i(t),u(t);(6)i(t),i(t)LLCCR1LCLCR3R1R2。khaw.com+u−LiR1+uR1−x2R1ii++CR2xR3uR31CR2−−图题9.1答案解本题说明状态变量的选取不是唯一的。若各组变量之间存在着非奇异线性变换关系，则这些变量组即可作为状态变量。又因为研究的是电路的状态，故可采取无激励电路（即令电路中的激励均为零）。i(t)=x(t)（1）L2u()t=x(t)−Rx(t)L132⎡iL(t)⎤⎡01⎤⎡x1(t)⎤⎢⎥=⎢⎥⎢⎥u(t)1−Rx(t)即⎣L⎦⎣3⎦⎣2⎦khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com11i(t)=−x(t)−x(t)−x(t)=C112RR（2）1211−(+)x(t)−x(t)12RR12ut)(=x(t)C1⎡11⎤⎡iC(t)⎤⎢−(+)1⎥⎡x1(t)⎤⎢⎥=⎢R1R2⎥⎢⎥⎣uC(t)⎦10⎣x2(t)⎦即khaw.com⎣⎦u=−xt)(（3）R11u()t=x(t)−Rx(t)L132⎡uR1(t)⎤⎡10⎤⎡x1(t)⎤⎢⎥=⎢⎥⎢⎥即⎣uL(t)⎦⎣1−R3⎦⎣x2(t)⎦11i(t)=−(+)x(t)−x(t)C12RR（4）12u(t)=x(t)−Rxt)(L132即⎡11⎤⎡iC(t)⎤⎢−(+)−1⎥⎡x1(t)⎤⎢⎥=⎢R1R2⎥⎢⎥⎣uL(t)⎦1−R⎣x2(t)⎦⎣3⎦11i(t)=−(+)x(t)−x(t)C12RR（5）12u()t=Rx(t)R332khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com即⎡11⎤⎡iC(t)⎤⎢−(+)−1⎥⎡x1(t)⎤⎢⎥=⎢R1R2⎥⎢⎥⎣uR3(t)⎦0R⎣x2(t)⎦⎣3⎦可见以上5对变量的变换矩阵，其行列式的值均不为零，即它们均为非奇异矩阵，故以上的五对变量组均可作为该电路的状态变量。1i(t)=−x(t)R11Rkhaw.com（6）11iR2(t)=x1(t)R2⎡1⎤−0⎡iR1(t)⎤⎢R1⎥⎡x1(t)⎤⎢⎥=⎢1⎥⎢⎥⎣iR2(t)⎦⎢0⎥⎣x2(t)⎦即⎢⎣R2⎥⎦i(t)i(t)可见此变换矩阵的行列式的值为零，故R1与R2不能同时作为状态变量，它们两者线性相关。x(t),x(t),x(t)9.2图题9.2所示电路，以123为状态变量，试列写电路的状态方程，并写成矩阵形式。2Ωx11HN1Hx22Ω++Ⅰ2F+Ⅱft1()x3ft2()−−−图题9.2答案khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com解只含一个独立电感的两个回路，ΙΠ分别列写ＫＶＬ方程为2x(t)+1ẋ()t+x(t)=f(t)11311ẋ(t)+2x(t)−x(t)=−f(t)2232⎧ẋ1(t)=−2x(1)t−x3(t)+f1(t)⎨ẋ(t)=−2x()t+x(t)−f(t)即⎩1232（1）（khaw.com2）对只含一个独立电容的节点Ｎ列写ＫＣＬ方程为2ẋ(t)=x(t)−x(t)31211ẋ(t)=x(t)−x(t)312即22（３）式（１），（２），（３，）即为电路的状态方程，其矩阵形式为⎡⎤⎡ẋ1(t)⎤⎢−201⎥⎡10⎤⎢⎥⎢⎥⎡f1(t)⎤ẋ(t)=⎢0−21⎥+0−1⎢2⎥⎢⎥⎢⎥⎢f(t)⎥11⎣2⎦⎢⎣ẋ3(t)⎥⎦⎢−0⎥⎢⎣00⎥⎦⎣22⎦9.3图题9.3所示电路，以x1(t),x2(t),x3(t)为状态变量，以y1(t),y2t)(为响应变量，试列写电路的状态方程与输出方程。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com+−i1Ω1ibc2da++x2−+x3−+x11ft1()ⅠH1Ωyt2()2−−gie3f图题9.3khaw.com答案解（１）求状态方程。对只含一个独立电感的回路列写ＫＶＬ方程为1x(t)+ẋ(t)=f(t)212ẋ(t)=−2x(t)+2f(t)即12（１）x(t)+x(t)23i==x(t)+x(t)123又1i=i+1(ẋ)t=x()t+x(t)+ẋ(t)213233abcdefga回路的ＫＶＬ方程为xt)(+x(t)+1i=f(t)232x(t)+x(t)+1[x()t+x()t+ẋ(t)]=f(t)即23233ẋ(t)=−2x(t)−2x(t)+f(t)故323（２）khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comẋ()t=x(t)+ż(t)=对节点b列ＫＣＬ方程为213x(t)−2x(t)−2xt)(+f(t)123（３）式（１），（２），（３）即为电路的状态评论员，其矩阵形式为⎡ẋ1(t)⎤⎡0−20⎤⎡x1(t)⎤⎡2⎤⎢ẋ(t)⎥=⎢1−2−2⎥⎢x(t)⎥+⎢1⎥[f(t)]⎢2⎥⎢⎥⎢2⎥⎢⎥khaw.com⎢⎣ẋ3(t)⎥⎦⎢⎣0−2−2⎥⎦⎢⎣x3(t)⎥⎦⎢⎣1⎥⎦（２）求输出方程。y(t)=x(t)+x(t)y(t)=−x(t)−x(t)+ft)(123223故输出方程的矩阵形式为⎡x1(t)⎤⎡y1(t)⎤⎡011⎤⎢⎥⎡0⎤[]⎢⎥=⎢⎥⎢x2(t)⎥+⎢⎥f(t)⎣y2(t)⎦⎣0−1−1⎦⎣1⎦⎢x(t)⎥⎣3⎦9.4以知系统的微分方程为y′′′(t)+5y′′(t)+7y′(t)+3y(t)+f(t)试列写系统的状态方程与输出方程，并写出Ａ，Ｂ，Ｃ，Ｄ矩阵。答案解从已知的系统微分方程列写系统状态方程与输出方程的题目。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com设状态变量为x(t)=y(t)1x()t=y(′t)=ẋ(t)21x()t=y(′′t)=ẋ(t)32代入原微分方程有ẋ(t)+5ẋt)(+7ẋ(t)+3x(t)=ft)(3211khaw.comẋ(t)=−3xt)(−5ẋt)(−7ẋt)(+f(t)即3121ẋ(t)=−3x(t)−7x(t)−5x(t)+f(t)即3123故得系统的状态方程为⎧ẋ1(t)=x2(t)⎪⎨ẋ2(t0=x3(t)⎪⎩ẋ(t)=−3x(t)−7x(t)−5x(t)+f(t)3123其矩阵形式为⎡ẋ1(t)⎤⎡010⎤⎡x1(t)⎤⎡0⎤⎢ẋ(t)⎥=⎢001⎥⎢x(t)⎥+⎢0⎥[f(t)]⎢2⎥⎢⎥⎢2⎥⎢⎥⎢ẋ(t)⎥⎢−3−7−5⎥⎢x(t)⎥⎢1⎥⎣3⎦⎣⎦⎣3⎦⎣⎦系统输出方程为⎡x1(t)⎤⎢⎥y(t)=x(t)=[100x](t)+0f(t)[][]1⎢2⎥⎢⎣x3(t)⎥⎦khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com⎡010⎤⎡0⎤⎢⎥⎢⎥A=001,B=0⎢⎥⎢⎥⎢⎣−3−7−5⎥⎦⎢⎣1⎥⎦C=[100],D=[]0故有9.5图题9.5所示系统，以积分器的输出信号为状态变量，试列写系统的khaw.com状态方程与输出方程。ẋx11∑∫4−3ẋx22ft)(∑∫1∑yt)(−2ẋ3x3∑∫−2−5图题5.9答案ẋ(t)=−3x(t)+f(t)ẋ(t)=−2x(t)+f(t)解1122ẋ(t)=−5x(t)+f(t)33此方程组即为系统的状态方程，其矩阵形式为khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com⎡ẋ1(t)⎤⎡−300⎤⎡x1(t)⎤⎡1⎤⎢ẋ(t)⎥=⎢0−20⎥⎢x(t)⎥+⎢1⎥[f(t)]⎢2⎥⎢⎥⎢2⎥⎢⎥⎢⎣ẋ3(t)⎥⎦⎢⎣00−5⎥⎦⎢⎣x3(t)⎥⎦⎢⎣1⎥⎦y(t)=4x(t)+x(t)−2x(t)系统的输出方程为123写成矩阵形式为⎡x1(t)⎤[][⎢⎥]y(t)=41−2x(t)khaw.com⎢2⎥⎢⎣x3(t)⎥⎦9.6已知系统的微分方程为y′′′(t)+7y′′(t)+10y′(t)=5f′(t)+5f(t)（１）试画出直接形式、级联形式、并联形式的信号流图；（2）列写出与上述各种形式相对应的状态方程与输出方程。答案5s+5解系统函数H(s)=32s+7s+10skhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com51ẋs−1xs−1s−11335F(s)Y(s)xx21−7−10(a)1s−1−15111ẋ1sx11F(s)Y(s)xẋxẋ2233−2−5(b)−1khaw.coms1152−1F(s)11s61Y(s)ẋx22−241−1−s3xẋ33−5(c)图题6.9（1）直接形式的信号流图如图9.6(a)所示。取积分器的输出信号x(t),x(t),x(t)123为状态变量，故可列写出系统的状态方程为ẋ(t)=x(t)12ẋ(t)=x(t)23ẋ(t)=−10x(t)−7x(t)+f(t)323其矩阵形式为⎡ẋ1(t)⎤⎡010⎤⎡x1(t)⎤⎡0⎤⎢⎥⎢⎥⎢⎥⎢⎥ẋ(t)=001x(t)+0[f(t)]⎢2⎥⎢⎥⎢2⎥⎢⎥⎢⎣ẋ3(t)⎥⎦⎢⎣0−10−7⎥⎦⎢⎣x3(t)⎥⎦⎢⎣1⎥⎦其输出方程为yt)(=5xt)(+5xt)(12khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com⎡x1(t)⎤[y(t)=]5[50⎢x(t)]⎥⎢2⎥即⎢⎣x3(t)⎥⎦5s+55(s+1)1s+11(2)H(s)===5×××32s+7s+10ss(s+2)(s+5)ss+2s+5故级联形式的信号流图如图题9.6（b）所示。取积分器的输出信号x(t),x(t),x(t)khaw.com123为状态变量，故可列写出系统的状态方程为ẋ(t)=−5x()t+x(t)+ẋ(t)=1122−5x(t)+x(t)−2x(t)+x(t)=ẋ(t)=−2x(t)+x(t)1223223−5x()t−x(t)+x(t)ẋ(t)=5f(t)1233其矩阵形式为⎡ẋ1(t)⎤⎡−5−11⎤⎡x1(t)⎤⎡0⎤⎢⎥⎢⎥⎢⎥⎢⎥ẋ(t)=0−21x(t)+0[f(t)]⎢2⎥⎢⎥⎢2⎥⎢⎥⎢⎣ẋ3(t)⎥⎦⎢⎣000⎥⎦⎢⎣x3(t)⎥⎦⎢⎣5⎥⎦其输出方程为y(t)=x(t)1⎡x1(t)⎤[][⎢]⎥y(t)=100x(t)⎢2⎥即⎢⎣x3(t)⎥⎦（3）153−5s+5264H(s)==++s(s+2)(s+5)ss+2s+5x(t),x(t),x(t)故并联形式的信号流图如图题9.6(c)所示。取积分器的输出信号123为状态变量，故可列写出系统的状态方程为khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comẋt)(=ft)(1ẋt)(=−2xt)(+ft)(22ẋ(t)=−5x(t)+f(t)33其矩阵形式为⎡ẋ1(t)⎤⎡000⎤⎡x1(t)⎤⎡1⎤⎢ẋ(t)⎥=⎢0−20⎥⎢x(t)⎥+⎢1⎥[f(t)]khaw.com⎢2⎥⎢⎥⎢2⎥⎢⎥⎢⎣ẋ3(t)⎥⎦⎢⎣00−5⎥⎦⎢⎣x3(t)⎥⎦⎢⎣1⎥⎦其输出方程为154y(t)=x(t)+x(t)−x(t)123263即⎡x1(t)⎤[]⎡153⎤⎢⎥y(t)=−x(t)⎢264⎥⎢2⎥⎣⎦⎢x(t)⎥⎣3⎦9.7已知离散系统的框图如图题9.7所示，试列写系统的状态方程与输出方程。W(z)X2(z)−1z+1X1(z)F(z)∑∑Y(z)+z−1z+3+−−2X3(z)z+1z−2图题9.7khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com答案x(k),x(k),x(k)解（1）状态方程。取一阶子系统的输出信号123为状态变量。W(z)=−2X()z−X(z)+F(z)23ω(k)=−2x(k)−x(k)+f(k)即231khaw.comX2(z)=W(z)又z−1zX(z)=X(z)+W(z)故22即x(k+1)=x(k)−(2x)k−(x)k+(f)k=−x()k−x(k)+f(k)222323（1）z+1X(z)=X(z)12又z+3故zX(z)=−3X(z)+2X(z)+X(k)1122故x1(k+1)=−3x1(k)+x2(k+1)+x2−(k)=−3x1(k)−x2(k)−x3(k)+f(k)+x2(k)=−3x()k−x(k)+f(k)13（2）z+1X(z)=X(z)31又z−2khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com故zX(z)=2X()z+zX(z)+X(z)3311故x(k+1)=2x(k)+x(k+1)+x(k)=2x(k)−3(x)k−x()k+f(k)+x(k)=33113131−2x(k)+x(k)+f(k)13（3）khaw.com将式（1），（2），（3）按次写成矩阵形式即为⎡x1(k+1)⎤⎡−30−1⎤⎡x1(k)⎤⎡1⎤⎢x(k+1)⎥=⎢0−1−1⎥⎢x(k)⎥+⎢1⎥[f(k)]⎢2⎥⎢⎥⎢2⎥⎢⎥⎢⎣x3(k+1)⎥⎦⎢⎣−201⎥⎦⎢⎣x3(k)⎥⎦⎢⎣1⎥⎦（１）输出方程为(Y)z=X(z)−X(z)12即(y)k=x(k)−x(k)12即⎡x1(k)⎤⎢⎥[y(k)=][10−1x(]k)⎢2⎥⎢⎣x3(k)⎥⎦9.8离散系统的时域模拟图如图题9.8所示，以单位延时器的输出信号x(k),x(k)12的状态变量，列写系统的状态方程与输出方程。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com−3−1x(k)1f(k)∑Dx(k+)1∑y(k)1−27x(k)∑D2x(k+)124khaw.com图题8.9答案解x(k+1)=−2x(k)+f(k)11x(k+1)=4x(k)+f(k)22其矩阵形式的状态方程为⎡x1(k+1)⎤⎡−20⎤⎡x1(k)⎤⎡1⎤[]⎢⎥=⎢⎥⎢⎥+⎢⎥f(k)⎣x2(k+1)⎦⎣04⎦⎣x2(k)⎦⎣1⎦其输出方程为y(k)=−x(k+)1+7x(k+)1−3f(k)12即y(k)=2x(k)+28x(k)+3f(k)12其矩阵形式的输出方程为khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com[][⎡x1(]k)⎤[][]y(k)=228⎢⎥+3f(k)x(k)⎣2⎦9.9已知离散系统的差分方程为khaw.comy(k)+3y(k−1)+2y(k−2)+y(k−3)=f(k−1)+2f(k−2)+3f(k−3)（1）画出系统直接形式的信号流图；（2）以单位延时器的输出信号x(t),x(t),x(t)123为状态变量，列写出系统的状态方程与输出方程。答案解（1）由差分方程可求得系统函数为2z+2z+3H(1)=32z+3z+121x3(k+)1−1−1−1zzzF(z)x(k)3x(k)x(k)−321−2−1图题9.9故直接形式的信号流图如图题9.9所示。以单位延时器的输出信号x(t),x(t),x(t)123为状态变量，可列写出状态方程为khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comx(k+1)=x(k)12x(k+1)=x(k)23x(k+1)=−x(k)−2x(k)−3x(k)+f(k)3123其矩阵形式为⎡x1(k+1)⎤⎡010⎤⎡x1(k)⎤⎡0⎤⎢x(k+1)⎥=⎢001⎥⎢x(k)⎥+⎢0⎥[f(k)]⎢2⎥⎢⎥⎢2⎥⎢⎥⎢⎣x3(k+1)⎥⎦⎢⎣−1−2−3⎥⎦⎢⎣x3(k)⎥⎦⎢⎣1⎥⎦其输出方程为khaw.comy(k)=3x(k)+2x(k)+x(k)123其矩阵形式为⎡x1(k)⎤[y(k)=][321⎢x(]k)⎥+0f(k[][)]⎢2⎥⎢x(k)⎥⎣3⎦9.10已知系统的状态转移矩阵为⎡−t−t⎤e(cost+sint)−2esintΦ(t)=⎢−t−t⎥⎣esinte(cost−sint)⎦求系统矩阵A。答案解方法一利用状态转移矩阵的一阶导数求，即dAtAte=Ae=AI=Adtt=0khdaw.comt=0若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com故⎡d−td−t⎤e(cost+sint)(−2esint)d⎢dtdt⎥A=Φ(x)=⎢⎥=dtd−td−tt=0⎢esinte(cost−sint)⎥⎣dtdt⎦t=0−t−t−t⎡−2esint2esint−2ecost⎤⎡0−2⎤⎢−t−t−t⎥=⎢⎥⎣−esint+ecost−2ecost⎦t=0⎣1−2⎦khaw.com方法二变换域方法因有[At][]−1Le=LΦ(t)=(sI−A)故[]−1A=sI−(LΦ(t))令⎡s+2−2⎤⎢22⎥(s+1)+1(s+1)+1L[Φ(t)=]⎢⎥=1s⎢⎥22⎢⎣(s+1)+1(s+1)+1⎥⎦1⎡s+2−2⎤2⎢⎥(s+1)+1⎣1s⎦故−1−1⎛1⎡s+2−2⎤⎞⎡s2⎤(L[Φ(t))]=⎜⎜2⎢⎥⎟⎟=⎢⎥⎝(s+1)+1⎣1s⎦⎠⎣−1s+2⎦故⎡s−s−2⎤⎡0−2⎤[−]1A=sI−(LΦ(t))=⎢⎥=⎢⎥⎣1s−s−2⎦⎣1−2⎦khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com9.11已知系统的状态方程为⎡ẋ1(t)⎤⎡−11⎤⎡x1(t)⎤⎡1⎤[]⎢⎥=⎢⎥⎢⎥+⎢⎥f(t)ẋ(t)0−2x(t)−1⎣2⎦⎣⎦⎣2⎦⎣⎦−−t⎡x1(0)⎤⎡1⎤激励f()t=eU(t)，初始状态为⎢−⎥=⎢⎥khaw.com⎢⎣x2(0)⎥⎦⎣2⎦。⎡x1(t)⎤(1)求系统的状态转移矩阵Φ(t；()2)求状态向量x(t)=⎢⎥⎣x2(t)⎦。答案⎡−11⎤⎡1⎤解（1）A=⎢⎥,B=⎢⎥⎣0−2⎦⎣−1⎦⎡11⎤⎢⎥[−1]s+1(s+1)(s+2)Φ(s)=sI−A=⎢⎥1⎢0⎥⎢⎣s+2⎥⎦故−t−t−2t⎡ee−e⎤Φ(t)=⎢⎥U(t)−2t⎣0e⎦⎡−t−−2t⎤3e2e−（2）零输入解=Φ(t)x(0)=⎢−2t⎥U(t)⎣2e⎦khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com⎡11⎤⎢s+1(s+1)(s+2)⎥⎡1⎤⎡1⎤⎢1⎥⎢⎥⎢⎥=⎢0⎥⎣−1⎦⎣s+2⎦⎢⎣s+2⎥⎦⎡1⎤⎡11⎤⎢(s+1)(s+2)⎥⎢−⎥=s+1s+2⎢⎥⎢⎥−1−11⎢⎥⎢+⎥s域零状态解=Φ(s)BF(s)=⎢⎣(s+1)(s+2)⎥⎦⎣s+1s+2⎦khaw.com−t−2t⎡4e−3e⎤故时域零状态解=⎢⎥U(t)−t−2t⎣−e+e⎦故得状态向量为x(t)−t−2t⎡1⎤⎡4e−3e⎤x(t)=⎢⎥=零输入解+零状态解=⎢−t−2t⎥U(t)⎣x2(t)⎦⎣−e+e⎦9.12已知系统的状态方程与输出方程为⎡xṫ1()⎤⎡xt1()⎤⎢⎥=A⎢⎥+B[ft()]⎣xṫ2()⎦⎣xt2()⎦⎡xt1()⎤[yt()=]C⎢⎥+D[ft()]⎣xt2()⎦khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com状态转移矩阵为−t−2t−t−2t⎡2e−e−2e+2e⎤Φ()t=⎢⎥U()t−t−2t−t−2t⎣e−e6e+2e⎦ft()=δ()t当激励时的零状态解与零状态响应分别为−t−2t⎡xt()⎤⎡12e−12e⎤1⎢⎥=⎢⎥U()t−t−2t⎣xt2()⎦⎣6e−12e⎦khaw.comA,B,C,D求系统的系数矩阵。答案解设⎡a11a12⎤⎡⎤b1A=⎢⎥,B=⎢⎥,C=[c1c2,D=]d[]aab⎣2122⎦⎣⎦2因有ddAtAtΦ()t=e=Aedtdt故−t−2t−t−2td⎡−2e+2e2e−4e⎤AtA=e=⎢⎥=−t−2t−t−2tdtt=0⎣−e+2ee−4e⎦t=0⎡0−2⎤⎢⎥⎣1−3⎦又有−t−2t−t−2t⎡xt()⎤⎡2e−e−2e+2e⎤⎡⎤b1At1⎢⎥=eB∗ft()=⎢⎥⎢⎥∗δ()t−t−2t−t−2t⎣xt2()⎦⎣e−e−e+2e⎦⎣⎦b1khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com即−t−2t−t−2t⎡12e−12e⎤⎡(2b−2)eb+−+(b2)eb⎤1212⎢⎥U()t=⎢⎥U()t−t−2t−t−2t⎣6e−12e⎦⎣(b−b)e+−+(b2)eb⎦1212故有⎧2b−2b=1212⎨⎩−+b2b=−1212联解得khaw.comb1=0,b2=−6。故得矩阵⎡0⎤B=⎢⎥⎣−6⎦又因有yt()=Cx()t+Df()t=−t−2t⎡12e−12e⎤[c1c2⎢]−t−2t⎥+[][dδ()t]⎣6e−12e⎦即−t−2t−t−2tδ()(6et+−12e)=⎡(12c+6)ec−12(c+c)e⎤+dδ()t⎣1212⎦故有⎧12c+6c=612⎪⎪⎨12(c+c)12=12⎪⎪d=1⎩c=0,c=1,d=1联解得12。故得矩阵C=[01]D=1[]khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comp=−1,p=−3故得系统的自然频率为12。9.13已知系统的信号流图如图题9.13所示。(1)以积分器的输出信号xt(),xt()12为状态变量，列写系统的状态方程与输出方程；(2)求系统函数矩阵H()sh()t；(3)求单位冲激响应矩阵。khaw.com21s−1x11F1(s)Y1(s)1−131−1F(s)sx22Y(s)22−1答案解这是一个多输入多输出系统。(1)状态方程与输出方程xṫ()=2()xt+ft()−ft()1112xṫ()=3()xt−xt()+ft()2122其矩阵形式为⎡xṫ()⎤⎡20⎤⎡xt()⎤⎡1−1⎤⎡ft()⎤111⎢⎥=⎢⎥⎢⎥+⎢⎥⎢⎥⎣xṫ()⎦⎣3−1⎦⎣xt()⎦⎣01⎦⎣ft()⎦222输出方程为yt()=xt()+xt()112khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comyt()=2()xt22其矩阵形式为⎡yt1()⎤⎡11⎤⎡xt1()⎤⎡00⎤⎡ft1()⎤⎢⎥=⎢⎥⎢⎥+⎢⎥⎢⎥yt()01xt()00ft()⎣2⎦⎣⎦⎣2⎦⎣⎦⎣2⎦故⎡20⎤⎡1−1⎤⎡11⎤⎡00⎤A=⎢⎥,B⎢⎥,C⎢⎥,D⎢⎥khaw.com⎣3−1⎦⎣01⎦⎣02⎦⎣00⎦H()s(2)求系统函数矩阵−1H()s=CΦ()sB+D=CI[s−A]B+D=⎡2−12−1⎤++⎢⎥s−2s+1s−2s+1⎢⎥⎢2−12−1⎥++⎢⎣s−2s+1s−2s+1⎥⎦h()t(3)求系统的单位冲激响应矩阵2t−t−t2t⎡2e−e2e−2e⎤−1h()t=L[H()s=]⎢⎥U()t2t−t−t2t⎣2e−2e4e−2e⎦9.14已知离散系统的状态方程与输出方程为⎡xk(+1)⎤⎡01⎤⎡xk()⎤⎡⎤011⎢⎥=⎢⎥⎢⎥+⎢⎥[fk()]⎣xk(+1)⎦⎣−65⎦⎣xk()⎦⎣⎦122⎡yk1()⎤⎡11⎤⎡xk1()⎤⎢⎥=⎢⎥⎢⎥⎣yk()⎦⎣2−1⎦⎣xk()⎦22khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com系统的初始状态为⎡x1(0)⎤⎡⎤1⎢⎥=⎢⎥x(0)2⎣2⎦⎣⎦kΦ()k=Afk()0=x()k(1)求状态转移矩阵；(2)求激励时的状态向量和响应y()k向量。答案khaw.com解(1)−1−1Φ()[z=I−zA]=⎡3z2z−zz⎤−+⎢⎥z−2z−3z−1z−3⎢⎥⎢6z6z−2z3z⎥−+⎢⎣z−2z−3z−2z−3⎥⎦或kkkk−1⎡3(2)−2(3)−(2)+(3)⎤Φ()k=L[Φ()z=]⎢⎥U()kkkkk⎣6(2)−6(3)−2(2)+3(3)⎦fk()=0(2)当激励时,状态向量只有零输入解,响应向量只有零输入响应。状态向量为k⎡2⎤x()k=Φ()(0)kx=⎢⎥U()kk⎣2(2)⎦响应向量为k⎡3(2)⎤y()k=CΦ()(0)kx=⎢⎥U()k⎣0⎦khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com9.15已知系统的状态方程与输出方程为⎡xṫ()⎤⎡−12⎤⎡xt()⎤⎡⎤011⎢⎥=⎢⎥⎢⎥+⎢⎥[ft()]⎣xṫ()⎦⎣−1−4⎦⎣xt()⎦⎣⎦122⎡xt1()⎤[yt()=]11[⎢]⎥+1ft()[][]xt()⎣2⎦khaw.com⎡ω1(t)⎤今选新的状态向量w(t)=⎢⎥，它与原状态向量x(t)的关系为ω(t)⎣2⎦⎡2−1⎤x()t=⎢⎥w()t⎣−11⎦(1)求关于w(t)的状态方程与输出方程；x(0−)−⎡1⎤⎡3⎤(2)已知系统的初始状态为x(0)=⎢−⎥=⎢⎥，激励f(t)=δ(t)，求两种状态变量下的响应y(t)。x(0)2⎣2⎦⎣⎦答案解(1)−1⎡2−1⎤⎡11⎤w()t=⎢⎥x()t=⎢⎥x()t⎣−11⎦⎣12⎦故⎡wṫ1()⎤⎡11⎤⎡xṫ1()⎤⎢⎥=⎢⎥⎢⎥=⎣wṫ2()⎦⎣12⎦⎣xṫ2()⎦⎡11⎤⎡⎧⎪−12⎤⎡xt()⎤⎡⎤0⎫⎪1⎢⎥⎢⎨⎥⎢⎥+⎢⎥[ft()⎬]=⎣12⎦⎣⎩⎪−1−4⎦⎣xt()⎦⎣⎦1⎭⎪2khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com⎡−20⎤⎡wt()⎤⎡⎤11⎢⎥⎢⎥+⎢⎥[ft()]⎣0−3⎦⎣wt()⎦⎣⎦22⎡2−1⎤⎡wt()⎤1[ft()=]11[⎢]⎥⎢⎥+[][1ft()=]⎣−11⎦⎣wt()⎦2⎡wt1()⎤[10⎢]⎥+1ft()[][]wt()⎣2⎦x()tkhaw.com(2)当状态变量为时1⎡s+42⎤−1Φ()[s=sI−A]=⎢⎥(s+2)(s+3)⎣−1s+1⎦⎡12−9⎤+⎢⎥−s+2s+3X()s=Φ()(0)sx+Φ()sBF()s=⎢⎥⎢−69⎥+⎢⎣s+2s+3⎥⎦故得状态向量为−2t−3t⎡12e−9e⎤x()t=⎢⎥U()t−2t−3t⎣−6e+9e⎦响应向量为−2t−3t⎡12e−9e⎤−2ty()t=[11⎢]⎥+[][1δ()t=]6eU()t+δ()t−2t−3t⎣−6e+9e⎦w()t当状态向量为时−⎡11⎤−⎡⎤5w(0)=⎢⎥x(0)=⎢⎥⎣12⎦⎣⎦7khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com⎡1⎤−10−1⎧⎡10⎤⎡−20⎤⎫⎢s+2⎥Φ()[s=sI−A]=⎨s⎢⎥⎢−⎥⎬=⎢⎥⎩⎣01⎦⎣03⎦⎭⎢1⎥0⎣⎢s+3⎦⎥−W()s=Φ()(0)sw+Φ()sBF()s=⎡1⎤⎡1⎤00⎢s+2⎥⎡⎤5⎢s+2⎥⎡⎤1⎢⎥⎢⎥+⎢⎥⎢⎥[]1=⎢1⎥⎣⎦7⎢1⎥⎣⎦200khaw.com⎢⎣s+3⎥⎦⎢⎣s+3⎥⎦故−2t⎡wt()⎤⎡6e⎤1w()t=⎢⎥=⎢⎥U()t−3twt()9e⎣2⎦⎣⎦⎡wt1()⎤−2t[yt()=]10[⎢]⎥+1ft()=[][6eU()t]+δ()twt()⎣2⎦可见在两种不同的状态变量下,响应是完全相同的。fk()=δ()k9.16已知离散系统的模拟图如图题9.16所示。(1)求激励时的x()k状态向量；(2)求系统的差分方程。khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.comx(k+)1x(k)11∑D3y(k)f(k)4x(k+)1x(k)22∑D2图题.916khaw.com答案x()k解(1)求状态向量xk(),xk()取单位延时器得输出信号12为状态变量,则可列出状态方程为xk(+1)=xk()+fk()11xk(+1)=4()2()xk+xk+fk()212其矩阵形式为⎡xk(+1)⎤⎡10⎤⎡xk()⎤11⎢⎥=⎢⎥⎢⎥+[11][fk()]⎣xk(+1)⎦⎣42⎦⎣xk()⎦22输出方程为yk()=3()xk1即⎡xk1()⎤[yk()=]30[⎢]⎥⎣xk2()⎦khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com⎡z⎤0⎢⎥−1z−1Φ()[z=zI−A]z=⎢⎥⎢−4z4zz⎥+⎢⎣−z1z−2z−⎦2⎥Fz()=L[δ()k=]1因为系统得初始状态为零,故状态向量中只有零状态解,即⎡1⎤⎢⎥khaw.comz−1X()z=Φ()zBF()z=⎢⎥⎢−45⎥+⎢⎣−z1z−⎦2⎥故得状态向量为⎡1⎤x()k=LX[()z=]⎢⎥U(k−1)k−1⎢⎣−⎡⎣45(2)−⎤⎦⎥⎦yk()=3()xk=3(Uk−1)(2)由于1为零状态响应,故3Yz()=z−1故3Yz()z−13Hz()===Fz()1z−1故得系统得差分方程为yk(+1)−yk()=3()fkkhdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com9.17已知系统的信号流图如图题9.17所示。(1)以积分器的输出信号xt(),xt()12为状态变量，列写系统的状态方程与输出方程；(2)求系统的微分方f(t)=U(t)程；(3)已知激励时的全响应为115y(t)=(+e−t−e−3t)U(t)求系统的零输入响应y(t)与初始状态x(0−)；326x1−1−1khaw.com11s1s1F(s)Y(s)ẋ2x3ẋ1x1−4−3图题9.17答案解(1)列写系统得状态方程与输出方程xṫ()=−4()xt+xt()+ft()112xṫ()=−3()xt+ft()21即⎡xṫ()⎤⎡−41⎤⎡xt()⎤⎡⎤111⎢⎥=⎢⎥⎢⎥+⎢⎥[ft()]⎣xṫ()⎦⎣−30⎦⎣xt()⎦⎣⎦122输出方程为⎡xt1()⎤yt()=xt1()=[10⎢]⎥+0ft()[][]xt()⎣2⎦khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com故⎡−41⎤⎡⎤1A=⎢⎥,B=⎢⎥,C=[10]D=0[]⎣−30⎦⎣⎦1(2)−1s+1H()s=CI[s−A]B+D=2s+4s+1故得系统得微分方程为khaw.comyt′′()4()3()+yt′+yt=ft′()+ft()(3)零状态响应得像函数为11s+1133Ys()=HsFs()()=×=−f(s+1)(s+3)sss+3故得零状态响应为11−3tyt()=(−e)()Utf33yt()故又得零输入响应x为11−t5−3tyt()=yt()−yt()=(+e−e)()Utxf32611−3t1−t1−3t(−e)()Ut=(e−e)()U3322故13y(0)=0,y′(0)=−+=1xx22khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com又因y(0)=CIx(0)=0xy′(0)=CAIx(0)=1x即⎡10⎤⎡x1(0)⎤[10⎢]⎥⎢⎥=001x(0)khaw.com⎣⎦⎣2⎦⎡−41⎤⎡10⎤⎡x(0)⎤1[10⎢]⎥⎢⎥⎢⎥=1⎣−30⎦⎣01⎦⎣x(0)⎦2联解得⎡x1(0)⎤⎡⎤0⎢⎥=⎢⎥x(0)1⎣2⎦⎣⎦9.18已知系统的信号流图如图题9.18所示。试求K满足什么条件时系统为稳定。−1−2F1(s)11−1ẋ3sx31−1s−1ẋs−11F2(s)11Y(s)kẋxx221−1−1图题.918khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com答案xt(),xt(),xt()解取积分器得输出信号123为状态变量,故状态方程与输出方程为xṫ()=xt()12xṫ2()=k[−xt1()−xt3()+ft2()]−xt2()=−kxt()−xt()−kxt()+kft()khaw.com1232xṫ3()=−2()xt3−[xt2()+xt3()]=−xt2()3()即⎡xṫ1()⎤⎡010⎤⎡xt1()⎤⎡00⎤⎢⎥⎢⎥⎢⎥⎢⎥⎡ft1()⎤xṫ()=−k−1−kxt()+0k⎢⎥⎢2⎥⎢⎥⎢2⎥⎢⎥ft()⎣2⎦⎢⎣xṫ()⎥⎦⎢⎣0−1−3⎥⎢⎦⎣xt()⎥⎢⎦⎣10⎥⎦33故系统的特征多项式为32[sI−A=]s+4s+3s+3k罗斯阵列为3s1302s43k0112−3k0s3k00s3k故欲使系统为稳定系统,就必须有khdaw.com若侵犯了您的版权利益，敬请来信通知我们！℡www.khdaw.com 课后答案网www.khdaw.com⎧123−k>0⎪⎨⎪⎩3k>0故得0