1. 您所在位置：首页 > 给排水规范 > 设计规范 > 《大学物理学》第二版下册习题解答.doc

《大学物理学》第二版下册习题解答.doc 66页

  • 4.54 MB
  • 2022-04-22 11:23:30 发布

《大学物理学》第二版下册习题解答.doc

  • 66页
  • 当前文档由用户上传发布，收益归属用户
  1. 1、本文档共5页，可阅读全部内容。
  2. 2、本文档内容版权归属内容提供方，所产生的收益全部归内容提供方所有。如果您对本文有版权争议，可选择认领，认领后既往收益都归您。
  3. 3、本文档由用户上传，本站不保证质量和数量令人满意，可能有诸多瑕疵，付费之前，请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形，可联系本站下载客服投诉处理。
  4. 文档侵权举报电话：19940600175。
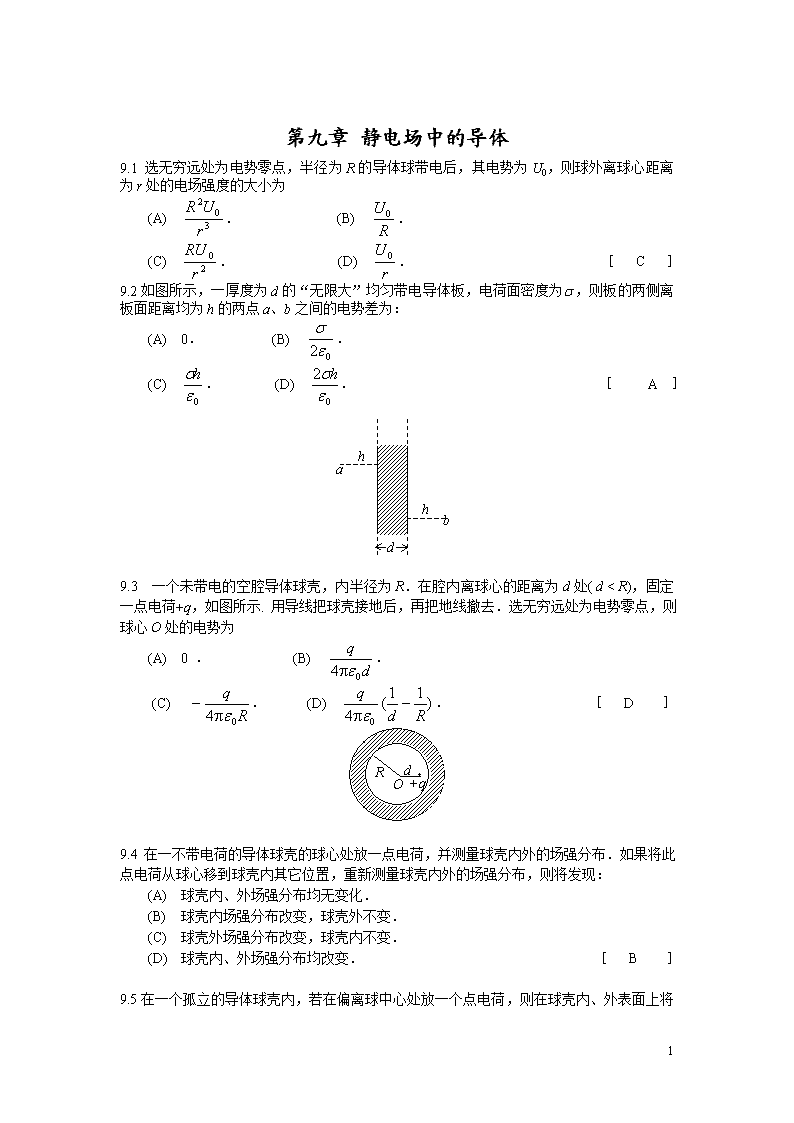
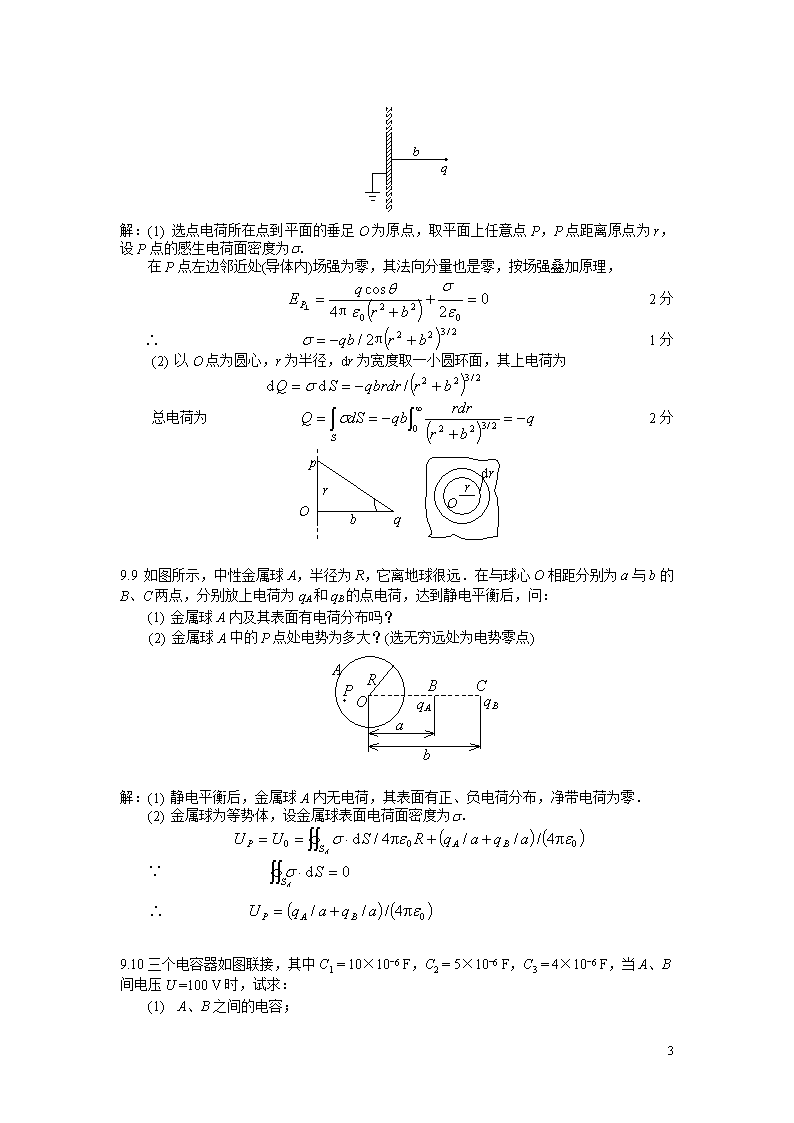
'第九章静电场中的导体9.1选无穷远处为电势零点，半径为R的导体球带电后，其电势为U0，则球外离球心距离为r处的电场强度的大小为(A)．(B)．(C)．(D)．［C］9.2如图所示，一厚度为d的“无限大”均匀带电导体板，电荷面密度为s，则板的两侧离板面距离均为h的两点a、b之间的电势差为：(A)0．(B)．(C)．(D)．［A］9.3一个未带电的空腔导体球壳，内半径为R．在腔内离球心的距离为d处(d>b，可以忽略边缘效应，求：(1)圆柱形电容器的电容；(2)电容器贮存的能量．解：由题给条件(和，忽略边缘效应,应用高斯定理可求出两筒之间的场强为：3分两筒间的电势差3分电容器的电容2分电容器贮存的能量2分10.17如图所示，一空气平行板电容器，极板面积为S，两极板之间距离为d，其中平行地放有一层厚度为t(tEx．说明如何操作,并需要知道什么数据才能得到测量结果.答：调节滑线电阻的滑动头M，使电流计G指示为零、即达到I=0．2分设这时FM间的电阻为Rx，则由含源电路欧姆定律得Ex=I0Rx若I0和Rx已知，则由上式可确定待测电动势Ex．3分第十二章稳恒磁场12.1均匀磁场的磁感强度垂直于半径为r的圆面．今以该圆周为边线，作一半球面S，则通过S面的磁通量的大小为(A)2pr2B．(B)pr2B．(C)0．(D)无法确定的量．［B］12.2载流的圆形线圈(半径a1)与正方形线圈(边长a2)通有相同电流I．若两个线圈的中心O1、O2处的磁感强度大小相同，则半径a1与边长a2之比a1∶a2为(A)1∶1(B)∶1(C)∶4(D)∶8［D］12.3如图，两根直导线ab和cd沿半径方向被接到一个截面处处相等的铁环上，稳恒电流66 I从a端流入而从d端流出，则磁感强度沿图中闭合路径L的积分等于(A)．(B)．(C)．(D)．［D］12.4在匀强磁场中，有两个平面线圈，其面积A1=2A2，通有电流I1=2I2，它们所受的最大磁力矩之比M1/M2等于(A)1．(B)2．(C)4．(D)1/4．［C］12.5如图，在一固定的载流大平板附近有一载流小线框能自由转动或平动．线框平面与大平板垂直．大平板的电流与线框中电流方向如图所示，则通电线框的运动情况对着从大平板看是：(A)靠近大平板．(B)顺时针转动．(C)逆时针转动．(D)离开大平板向外运动．［B］12.6无限长直导线在P处弯成半径为R的圆，当通以电流I时，则在圆心O点的磁感强度大小等于(A)．(B)．(C)0．(D)(E)．［D］66 12.7一载有电流I的细导线分别均匀密绕在半径为R和r的长直圆筒上形成两个螺线管，两螺线管单位长度上的匝数相等．设R=2r，则两螺线管中的磁感强度大小BR和Br应满足：(A)BR=2Br．(B)BR=Br．(C)2BR=Br．(D)BR=4Br．［B］12.8如图所示，一无限长直导线通有电流I=10A，在一处折成夹角q＝60°的折线，求角平分线上与导线的垂直距离均为r=0.1cm的P点处的磁感强度．(m0=4p×10-7H·m-1)解：P处的可以看作是两载流直导线所产生的，与的方向相同．3分3.73×10-3T1分方向垂直纸面向上．1分12.9如图所示，半径为R，线电荷密度为l(>0)的均匀带电的圆线圈，绕过圆心与圆平面垂直的轴以角速度w转动，求轴线上任一点的的大小及其方向．解：1分3分的方向与y轴正向一致．1分12.10均匀带电刚性细杆AB，线电荷密度为l，绕垂直于直线的轴O以w角速度匀速转动(O66 点在细杆AB延长线上)．求：(1)O点的磁感强度；(2)系统的磁矩；(3)若a>>b，求B0及pm．解：(1)对r～r+dr段，电荷dq=ldr，旋转形成圆电流．则2分它在O点的磁感强度1分2分方向垂直纸面向内．(2)1分2分方向垂直纸面向内．(3)若a>>b，则，过渡到点电荷的情况．　　　　　　　　　　　　　　　　　2分同理在a>>b时，，则也与点电荷运动时的磁矩相同．2分12.11如图所示，一半径为R的均匀带电无限长直圆筒，面电荷密度为s．该筒以角速度w绕其轴线匀速旋转．试求圆筒内部的磁感强度．解：如图所示，圆筒旋转时相当于圆筒上具有同向的面电流密度i，3分作矩形有向闭合环路如图中所示．从电流分布的对称性分析可知，在上各点66 的大小和方向均相同，而且的方向平行于，在和上各点的方向与线元垂直，在,上各点．应用安培环路定理2分可得2分圆筒内部为均匀磁场，磁感强度的大小为，方向平行于轴线朝右．1分12.12一根很长的圆柱形铜导线均匀载有10A电流，在导线内部作一平面S，S的一个边是导线的中心轴线，另一边是S平面与导线表面的交线，如图所示．试计算通过沿导线长度方向长为1m的一段S平面的磁通量．(真空的磁导率m0=4p×10-7T·m/A，铜的相对磁导率mr≈1)解：在距离导线中心轴线为x与处，作一个单位长窄条，其面积为．窄条处的磁感强度2分所以通过dS的磁通量为通过１m长的一段S平面的磁通量为Wb3分12.13在一顶点为45°的扇形区域，有磁感强度为方向垂直指向纸面内的均匀磁场，如图．今有一电子(质量为m，电荷为-e)在底边距顶点O为l的地方，以垂直底边的速度射入该磁场区域，若要使电子不从上面边界跑出，电子的速度最大不应超过多少？解：电子进入磁场作圆周运动，圆心在底边上．当电子轨迹与上面边界相切时，对应最大速度，此时有如图所示情形．66 ∴由，求出v最大值为12.14有一无限大平面导体薄板，自下而上均匀通有电流，已知其面电流密度为i(即单位宽度上通有的电流强度)．(1)试求板外空间任一点磁感强度的大小和方向．(2)有一质量为m，带正电荷q的粒子，以速度v沿平板法线方向向外运动(如图)，求：(a)带电粒子最初至少在距板什么位置处才不与大平板碰撞？(b)需经多长时间，才能回到初始位置(不计粒子重力)？解：(1)由安培环路定理：(大小)方向：在板右侧垂直纸面向里3分(2)由洛伦兹力公式可求(至少从距板R处开始向外运动)返回时间2分12.15一圆线圈的半径为R，载有电流I，置于均匀外磁场中(如图示)．在不考虑载流圆线圈本身所激发的磁场的情况下，求线圈导线上的张力．(载流线圈的法线方向规定与的方向相同．)66 解：考虑半圆形载流导线CD所受的安培力3分列出力的平衡方程式故：2分12.16半径为R的半圆线圈ACD通有电流I2，置于电流为I1的无限长直线电流的磁场中，直线电流I1恰过半圆的直径，两导线相互绝缘．求半圆线圈受到长直线电流I1的磁力．解：长直导线在周围空间产生的磁场分布为取xOy坐标系如图，则在半圆线圈所在处各点产生的磁感强度大小为：，方向垂直纸面向里，3分式中q为场点至圆心的联线与y轴的夹角．半圆线圈上dl段线电流所受的力为：3分．根据对称性知：Fy=，∴半圆线圈受I1的磁力的大小为：，方向：垂直I1向右．4分12.17如图，一半径为R的带电塑料圆盘，其中半径为r的阴影部分均匀带正电荷，面电荷密度为+s，其余部分均匀带负电荷，面电荷密度为-s。当圆盘以角速度w旋转时，测得圆盘中心O点的磁感强度为零，问R与r满足什么关系？解：带电圆盘转动时，可看作无数的电流圆环的磁场在O点的叠加．某一半径为r的圆环的磁场为2分66 而∴2分正电部分产生的磁感强度为2分负电部分产生的磁感强度为今∴2分12.18有一闭合回路由半径为a和b的两个同心共面半圆连接而成，如图．其上均匀分布线密度为l的电荷，当回路以匀角速度w绕过O点垂直于回路平面的轴转动时，求圆心O点处的磁感强度的大小．解：B1、B2分别为带电的大半圆线圈和小半圆线圈转动产生的磁感强度，B3为沿直径的带电线段转动产生的磁感强度．，3分，3分4分12.19已知半径之比为2∶1的两载流圆线圈各自在其中心处产生的磁感强度相等，求当两线圈平行放在均匀外场中时，两圆线圈所受力矩大小之比．解：设两圆线圈半径分别为R1，R2，分别通以电流I1，I2．则其中心处磁感强度分别为：，已知，∴2分设外磁场磁感强度为，两线圈磁矩和与夹角均为a，则两线圈所受力矩大小2分66 1分12.20在一平面内有三根平行的载流直长导线，已知导线1和导线2中的电流I1=I2流向相同，两者相距d，并且在导线1和导线2之间距导线1为a=d/3处B=0，求第三根导线放置的位置与所通电流I3之间的关系．解：取x坐标如图（原点在I1处）．设第三根导线放在与I1相距为x处，电流流向同于I1，则有02分即2分当I3与I1同方向时，第三根导线在B=0处的右侧，当I2与I1反方向时，第三根导线在B=0处的左侧．1分12.21如图，半径为a，带正电荷且线密度是l(常量)的半圆以角速度w绕轴O′O″匀速旋转．求：(1)O点的；(2)旋转的带电半圆的磁矩．(积分公式)解：(1)对q～q+dq弧元，，旋转形成圆电流2分它在O点的磁感强度dB为：66 3分1分的方向向上．1分(2)3分1分的方向向上．1分12.22如图，一无限长圆柱形直导体，横截面半径为R，在导体内有一半径为a的圆柱形孔，它的轴平行于导体轴并与它相距为b，设导体载有均匀分布的电流I，求孔内任意一点P的磁感强度B的表达式．解∶电流密度1分P点场强为充满圆柱并与I同向的电流I10，及充满孔并与I反向的电流I20的场叠加而成．取垂直于圆柱轴并包含P点的平面，令柱轴与孔轴所在处分别为O与O¢，P点与两轴的距离分别为r1与r2，并建立坐标如图．利用安培环路定理可知P点场强为与I同向的I1和与I反向的I2的场的叠加，且有，2分2分，方向如图所示．P点总场3分3分1分B与r1，r2无关，可知圆柱孔内为匀强场，方向沿y轴正向．66 12.23如图所示，有一电子以初速v0沿与均匀磁场成a角度的方向射入磁场空间．试证明当图中的距离时，(其中me为电子质量，e为电子电荷的绝对值，n=1，2……)，电子经过一段飞行后恰好打在图中的O点．证：设电子飞行时间为t，其作螺旋运动的周期为T，则：①1分②2分当t=nT时，电子能恰好打在O点．∴2分第十三章磁介质13.1关于稳恒电流磁场的磁场强度，下列几种说法中哪个是正确的？(A)仅与传导电流有关．(B)若闭合曲线内没有包围传导电流，则曲线上各点的必为零．(C)若闭合曲线上各点均为零，则该曲线所包围传导电流的代数和为零．(D)以闭合曲线Ｌ为边缘的任意曲面的通量均相等．［C］13.2磁介质有三种，用相对磁导率mr表征它们各自的特性时，(A)顺磁质mr>0，抗磁质mr<0，铁磁质mr>>1．(B)顺磁质mr>1，抗磁质mr=1，铁磁质mr>>1．66 (C)顺磁质mr>1，抗磁质mr<1，铁磁质mr>>1．(D)顺磁质mr<0，抗磁质mr<1，铁磁质mr>0．［C］13.3一均匀磁化的磁棒，直径为d＝25mm，长L＝75mm，磁矩为pm＝12000A·m2．求磁棒表面磁化电流密度iS．解：pm=iSLS3分S=pd2/4A/m2分13.4螺绕环中心周长l=10cm，环上均匀密绕线圈N=200匝，线圈中通有电流I=0.1A．管内充满相对磁导率mr=4200的磁介质．求管内磁场强度和磁感强度的大小．解：200A/m3分1.06T2分13.5一根沿轴向均匀磁化的细长永磁棒，磁化强度为，求图中标出各点的和．解：把磁棒看作nI=i"的无限长螺线管，则B1=m0i"=m0M，2分因螺线管无限长，∴2分和螺线管一样，在端面附近有2分介质棒内，，2分介质棒外，2分13.6一铁环中心线周长l=30cm，横截面S=1.0cm2，环上紧密地绕有N=300匝线圈．当导线中电流I=32mA时，通过环截面的磁通量F=2.0×10-5Wb．试求铁芯的磁化率cm．解：B=F/S=2.0×10-2T2分32A/m2分6.25×10-4T·m/A2分4962分13.7在磁化强度为的均匀磁化的无限大磁介质中，挖出一个半径为R的球形腔．求此腔表面的磁化电流面密度和磁化电流产生的磁矩．66 解：磁化电流面密度为：。式中是磁介质表面法线方向单位矢量，方向指向球心．设：M的方向与z轴重合，则j=Msinf，方向如图所示．3分选择一宽度为dl=Rdf的圆环，它产生的磁矩为：3分总磁矩为：3分方向与z轴方向相反，即与反向，写成矢量式为：1分13.8一根同轴线由半径为R1的长导线和套在它外面的内半径为R2、外半径为R3的同轴导体圆筒组成．中间充满磁导率为m的各向同性均匀非铁磁绝缘材料，如图．传导电流I沿导线向上流去，由圆筒向下流回，在它们的截面上电流都是均匀分布的．求同轴线内外的磁感强度大小B的分布．解：由安培环路定理：66 0R3区域：H=0，B=0第十四章电磁感应14.1半径为a的圆线圈置于磁感强度为的均匀磁场中，线圈平面与磁场方向垂直，线圈电阻为R；当把线圈转动使其法向与的夹角a=60°时，线圈中通过的电荷与线圈面积及转动所用的时间的关系是(A)与线圈面积成正比，与时间无关．(B)与线圈面积成正比，与时间成正比．(C)与线圈面积成反比，与时间成正比．(D)与线圈面积成反比，与时间无关．［A］14.2一矩形线框长为a宽为b，置于均匀磁场中，线框绕OO′轴，以匀角速度w旋转(如图所示)．设t=0时，线框平面处于纸面内，则任一时刻感应电动势的大小为66 (A)2abB|coswt|．(B)wabB(C)．(D)wabB|coswt|．(E)wabB|sinwt|．［D］14.3如图，长度为l的直导线ab在均匀磁场中以速度移动，直导线ab中的电动势为(A)Blv．(B)Blvsina．(C)Blvcosa．(D)0．［D］14.3圆铜盘水平放置在均匀磁场中，的方向垂直盘面向上．当铜盘绕通过中心垂直于盘面的轴沿图示方向转动时，(A)铜盘上有感应电流产生，沿着铜盘转动的相反方向流动．(B)铜盘上有感应电流产生，沿着铜盘转动的方向流动．(C)铜盘上产生涡流．(D)铜盘上有感应电动势产生，铜盘边缘处电势最高．(E)铜盘上有感应电动势产生，铜盘中心处电势最高．［D］14.5自感为0.25H的线圈中，当电流在(1/16)s内由2A均匀减小到零时，线圈中自感电动势的大小为：(A)7.8×10-3V．(B)3.1×10-2V．(C)8.0V．(D)12.0V．［C］14.6两个相距不太远的平面圆线圈，怎样可使其互感系数近似为零？设其中一线圈的轴线恰通过另一线圈的圆心．66 (A)两线圈的轴线互相平行放置．(B)两线圈并联．(C)两线圈的轴线互相垂直放置．(D)两线圈串联．［C］14.7面积为S和2S的两圆线圈1、2如图放置，通有相同的电流I．线圈1的电流所产生的通过线圈2的磁通用F21表示，线圈2的电流所产生的通过线圈1的磁通用F12表示，则F21和F12的大小关系为：(A)F21=2F12(B)F21>F12．(C)F21=F12．(D)F21=F12．［C］14.8用线圈的自感系数L来表示载流线圈磁场能量的公式(A)只适用于无限长密绕螺线管．(B)只适用于单匝圆线圈．(C)只适用于一个匝数很多，且密绕的螺绕环．(D)适用于自感系数Ｌ一定的任意线圈．［D］14.9有两个长直密绕螺线管，长度及线圈匝数均相同，半径分别为r1和r2．管内充满均匀介质，其磁导率分别为m1和m2．设r1∶r2=1∶2，m1∶m2=2∶1，当将两只螺线管串联在电路中通电稳定后，其自感系数之比L1∶L2与磁能之比Wm1∶Wm2分别为：(A)L1∶L2=1∶1，Wm1∶Wm2=1∶1．(B)L1∶L2=1∶2，Wm1∶Wm2=1∶1．(C)L1∶L2=1∶2，Wm1∶Wm2=1∶2．(D)L1∶L2=2∶1，Wm1∶Wm2=2∶1．［C］14.10真空中一根无限长直细导线上通电流I，则距导线垂直距离为a的空间某点处的磁能密度为(A)(B)(C)(D)［B］14.11一忽略内阻的电源接到阻值R＝10的电阻和自感系数L＝0.52H的线圈所组成的串联电路上，从电路接通计时，当电路中的电流达到最大值的90%倍时，经历的时间是：(A)46s．(B)0.46s．(C)0.12s(D)5.26×10-3s．［C］14.12一个自感系数为0.05mH，电阻为0.0166 的线圈连接到内阻可以忽略的电池上，则开关接通后经过_____________s，线圈中电流达到最大值的90％．(答0.0115)14.13电容器电容C=5mF，极板带有电荷Q=1×10-3C．通过一个R=1×106W的电阻放电，经历时间t=5s时电容器两极板间电势差为U=__________．（答73.6V）参考解：73.6V14.14如图，在电容器充电电路中，R=2000W，C=100mF，E=100V，则充电开始时的最大电流imax=___________．充电完毕时电容器上的电势差UC=_______________________．（答：50mA，100V）14.15在图示的电路中，R=2000W，C=100mF，E=100V，则电路的时间常数为_________．一般认为电容器的电势差uC达到最大值的99％以上为电容器充电完毕，则充电时间t应大于______．（答：0.2s，0.921s）14.16.如图所示，有一根长直导线，载有直流电流I，近旁有一个两条对边与它平行并与它共面的矩形线圈，以匀速度沿垂直于导线的方向离开导线．设t=0时，线圈位于图示位置，求(1)在任意时刻t通过矩形线圈的磁通量F．(2)在图示位置时矩形线圈中的电动势E．解：(1)3分(2)2分14.17如图所示，长直导线AB中的电流I沿导线向上，并以dI/dt=2A/s的变化率均匀增长．导线附近放一个与之同面的直角三角形线框，其一边与导线平行，位置及线框尺寸如图所示．求此线框中产生的感应电动势的大小和方向．(m0=4p×10-7T·m/A)。66 解：建立坐标如图所示，则直角三角形线框斜边方程y=-2x+0.2(SI)在直角三角形线框所围平面上的磁通量为＝2.59×10-8I(SI)三角形线框中的感应电动势大小为E=-dF/dt=-2.59×10-8(dI/dt)=–5.18×10-8V其方向为逆时针绕行方向．14.18一面积为S的单匝平面线圈，以恒定角速度w在磁感强度的均匀外磁场中转动，转轴与线圈共面且与垂直（为沿z轴的单位矢量）．设t=0时线圈的正法向与同方向，求线圈中的感应电动势．解：2分3分14.19如图所示，一半径为r2电荷线密度为l的均匀带电圆环，里边有一半径为r1总电阻为R的导体环，两环共面同心(r2>>r1)，当大环以变角速度w=w(t)绕垂直于环面的中心轴旋转时，求小环中的感应电流．其方向如何？解：大环中相当于有电流2分这电流在O点处产生的磁感应强度大小2分以逆时针方向为小环回路的正方向，2分∴66 2分方向：dw(t)/dt>0时，i为负值，即i为顺时针方向．1分dw(t)/dt<0时，i为正值，即i为逆时针方向．1分14.20电荷Q均匀分布在半径为a、长为L(L>>a)的绝缘薄壁长圆筒表面上，圆筒以角速度w绕中心轴线旋转．一半径为2a、电阻为R的单匝圆形线圈套在圆筒上(如图所示)．若圆筒转速按照的规律(w0和t0是已知常数)随时间线性地减小，求圆形线圈中感应电流的大小和流向．解：筒以w旋转时，相当于表面单位长度上有环形电流，它和通电流螺线管的nI等效．按长螺线管产生磁场的公式，筒内均匀磁场磁感强度为：(方向沿筒的轴向)4分筒外磁场为零．穿过线圈的磁通量为：2分在单匝线圈中产生感生电动势为2分感应电流i为1分i的流向与圆筒转向一致．1分14.21两个半径分别为R和r的同轴圆形线圈相距x，且R>>r，x>>R．若大线圈通有电流I而小线圈沿x轴方向以速率v运动，试求x=NR时(N为正数)小线圈回路中产生的感应电动势的大小．解：由题意，大线圈中的电流Ｉ在小线圈回路处产生的磁场可视为均匀的．66 3分故穿过小回路的磁通量为2分由于小线圈的运动，小线圈中的感应电动势为2分当x=NR时，小线圈回路中的感应电动势为1分B14.22如图所示，有一弯成q角的金属架COD放在磁场中，磁感强度的方向垂直于金属架COD所在平面．一导体杆MN垂直于OD边，并在金属架上以恒定速度向右滑动，与MN垂直．设t=0时，x=0．求下列两情形，框架内的感应电动势Ei．(1)磁场分布均匀，且不随时间改变．(1)非均匀的时变磁场．解：(1)由法拉第电磁感应定律：2分在导体MN内Ei方向由M向N．(2)对于非均匀时变磁场取回路绕行的正向为O→N→M→O，则3分Ei=3分66 Ei>0，则Ei方向与所设绕行正向一致，Ei<0，则Ei方向与所设绕行正向相反14.23如图所示，真空中一长直导线通有电流I(t)=I0e-lt(式中I0、l为常量，t为时间)，有一带滑动边的矩形导线框与长直导线平行共面，二者相距a．矩形线框的滑动边与长直导线垂直，它的长度为b，并且以匀速(方向平行长直导线)滑动．若忽略线框中的自感电动势，并设开始时滑动边与对边重合，试求任意时刻t在矩形线框内的感应电动势Ei并讨论Ei方向．解：线框内既有感生又有动生电动势．设顺时针绕向为Ei的正方向．由Ei=-dF/dt出发，先求任意时刻t的F(t)2分2分再求F(t)对t的导数：∴Ei4分Ei方向：lt<1时，逆时针；lt>1时，顺时针．2分[动生电动势、感生电动势]14.24载有电流的I长直导线附近，放一导体半圆环MeN与长直导线共面，且端点MN的连线与长直导线垂直．半圆环的半径为b，环心O与导线相距a．设半圆环以速度平行导线平移，求半圆环内感应电动势的大小和方向以及MN两端的电压UM-UN．66 解：动生电动势为计算简单，可引入一条辅助线MN，构成闭合回路MeNM,闭合回路总电动势，2分负号表示的方向与x轴相反．方向N→M14.25求长度为L的金属杆在均匀磁场中绕平行于磁场方向的定轴OO＇转动时的动生电动势．已知杆相对于均匀磁场的方位角为q，杆的角速度为w，转向如图所示．解：在距O点为l处的dl线元中的动生电动势为dE66 ∴EE的方向沿着杆指向上端．14.26如图所示，一长直导线中通有电流I，有一垂直于导线、长度为l的金属棒AB在包含导线的平面内，以恒定的速度沿与棒成q角的方向移动．开始时，棒的A端到导线的距离为a，求任意时刻金属棒中的动生电动势，并指出棒哪端的电势高．解：1分Ei(指向以A到B为正)3分式中：2分A端的电势高．2分14.27如图所示，长直导线中电流为i，矩形线框abcd与长直导线共面，且ad∥AB，dc边固定，ab边沿da及cb以速度无摩擦地匀速平动．t=0时，ab边与cd边重合．设线框自感忽略不计．(1)如i=I0，求ab中的感应电动势．ab两点哪点电势高？(2)如i=I0coswt，求ab边运动到图示位置时线框中的总感应电动势．66 解：(1)所处的磁场不均匀，建立坐标ox，x沿ab方向，原点在长直导线处，则x处的磁场为，i=I02分沿a→b方向3分故1分(2)，以abcda作为回路正方向，2分上式中，则有4分14.28如图所示，一根长为L的金属细杆ab绕竖直轴O1O2以角速度w在水平面内旋转．O1O2在离细杆a端L/5处．若已知地磁场在竖直方向的分量为．求ab两端间的电势差．解：间的动生电动势：4分b点电势高于O点．间的动生电动势：4分66 a点电势高于O点．∴2分14.29长为L，质量为m的均匀金属细棒，以棒端O为中心在水平面内旋转，棒的另一端在半径为L的金属环上滑动．棒端O和金属环之间接一电阻R，整个环面处于均匀磁场中，的方向垂直纸面向里，如图．设t=0时，初角速度为w0．忽略摩擦力及金属棒、导线和圆环的电阻．求(1)当角速度为w时金属棒内的动生电动势的大小．(2)棒的角速度随时间变化的表达式．解∶(1)3分(2)①2分②1分3分3分其中exp(x)=ex14.30在两根平行放置相距2a的无限长直导线之间，有一与其共面的矩形线圈，线圈边长分别为l和2b，且l边与长直导线平行．两根长直导线中通有等值同向稳恒电流I，线圈以恒定速度垂直直导线向右运动(如图所示)．求：线圈运动到两导线的中心位置(即线圈的中心线与两根导线距离均为a)时，线圈中的感应电动势．66 解：取顺时针方向回路正向．2分2分2分∴2分14.31在半径为R的圆柱形空间内，存在磁感强度为的均匀磁场，的方向与圆柱的轴线平行．有一无限长直导线在垂直圆柱中心轴线的平面内，两线相距为a，a>R，如图所示．已知磁感强度随时间的变化率为dB/dt，求长直导线中的感应电动势E，并说明其方向．解：由问题的轴对称性和轴向的无限长条件可知，感生涡漩电场的场强在垂直轴线的平面内，且与径向相垂直．3分如图所示，选取过轴线而平行给定的无限长直导线的一条无限长直导线，与给定的无限长直导线构成闭合回路(在无限远闭合)，则在过轴线的长直导线上，因处处与之垂直，∴电动势为零．又在无限远处，故此回路中的电动势就是给定的无限长直导线中的电动势E．3分该回路的磁通量1分由电磁感应定律有：2分E的正方向如图所示．1分14.32在一无限长载有电流I的直导线产生的磁场中，有一长度为b的平行于导线的短铁棒，它们相距为a．若铁棒以速度垂直于导线与铁棒初始位置组成的平面匀速运动，求t时刻铁棒两端的感应电动势E的大小．66 解：如俯视图所示14.33图中所示为水平面内的两条平行长直裸导线LM与L′M′，其间距离为l，其左端与电动势为E0的电源连接．匀强磁场垂直于图面向里．一段直裸导线ab横嵌在平行导线间(并可保持在导线间无摩擦地滑动)把电路接通．由于磁场力的作用,ab将从静止开始向右运动起来．求(1)ab能达到的最大速度v．(2)ab达到最大速度时通过电源的电流I．解：(1)导线ab运动起来时，切割磁感线，产生动生电动势．设导线中电流为i，导线运动速度为v，则ab上的动生电动势E=Blv，由b指向a．2分在由ab接通的电路中E0-E=E0-Blv=ri在磁场力作用下，v不断增大，则i不断减小，当v增大到某一值V时，2分若E0-BlV=0，则i=0，ab所受磁场力为零，其速度不再增加，导线作匀速运动，这也就是ab能达到的最大速度V=E0/(Bl)2分(2)这时电路中和电源中的电流都是I=02分[自感和互感]14.34真空矩形截面螺绕环的总匝数为N，尺寸如图所示，求它的自感系数．解：设螺绕环中通电流I，在环内取以环中心为圆心，半径为r的圆形回路，由安培环路定理有66 则3分通过螺线管矩形截面的磁通链数Y为：3分∴2分14.35两同轴长直螺线管，大管套着小管，半径分别为a和b，长为L(L>>a；a>b)，匝数分别为N1和N2，求互感系数M．解：设半径为a的长螺线管中通入电流I，则管内的均匀磁场1分通过半径为b的线圈横截面积的磁通量为：通过半径为b的长螺线管的磁链为：2分根据定义：2分14.36一无限长直导线通有电流．一矩形线圈与长直导线共面放置，其长边与导线平行，位置如图所示．求：(1)矩形线圈中感应电动势的大小及感应电流的方向；(2)导线与线圈的互感系数．解：(1)1分1分∴2分2分感应电流方向为顺时针方向．2分(2)2分10一矩形线圈长a=0.20m，宽b=0.10m，由10066 匝表面绝缘的细导线绕成，放在一很长的直导线旁且与之共面，线圈的长边与长直导线平行，导线和线圈间的距离为b，如图．求它们之间的互感．(真空的磁导率m0=4p×10-7H/m)解：设长直导线中有电流I，它在周围产生磁场1分在矩形线圈中产生的磁通链数为3分H1分14.37真空中，一个半径r1=1cm，长度l1=1m的圈数为N1=1000的螺线管在它的中部与它同轴有一个半径r2=0.5cm，长度l2=1.0cm圈数N2=10的小线圈．计算两个线圈的互感系数．(真空的磁导率m0=4p×10-7H/m)解：设外圈线圈通过电流I1，由于l1>>r1，它在线圈中间产生的磁感强度为：1分由于内线圈的r2

您可能关注的文档

相关文档

最近下载