张仰森---人工智能原理及其应用(第二版)习题答案.doc 35页

'第2章知识表示方法部分参考答案2.8设有如下语句，请用相应的谓词公式分别把他们表示出来：(1)有的人喜欢梅花，有的人喜欢菊花，有的人既喜欢梅花又喜欢菊花。解：定义谓词P(x)：x是人L(x,y)：x喜欢y其中，y的个体域是{梅花，菊花}。将知识用谓词表示为：(x)(P(x)∧(L(x,梅花)∨L(x,菊花)∨L(x,梅花)∧L(x,菊花)))(2)有人每天下午都去打篮球。解：定义谓词P(x)：x是人B(x)：x打篮球A(y)：y是下午将知识用谓词表示为：(x)(y)(A(y)∧B(x)∧P(x))(3)新型计算机速度又快，存储容量又大。解：定义谓词NC(x)：x是新型计算机F(x)：x速度快B(x)：x容量大将知识用谓词表示为：(x)(NC(x)→F(x)∧B(x))(4)不是每个计算机系的学生都喜欢在计算机上编程序。解：定义谓词S(x)：x是计算机系学生L(x,pragramming)：x喜欢编程序U(x,computer)：x使用计算机将知识用谓词表示为：¬(x)(S(x)→L(x,pragramming)∧U(x,computer))(5)凡是喜欢编程序的人都喜欢计算机。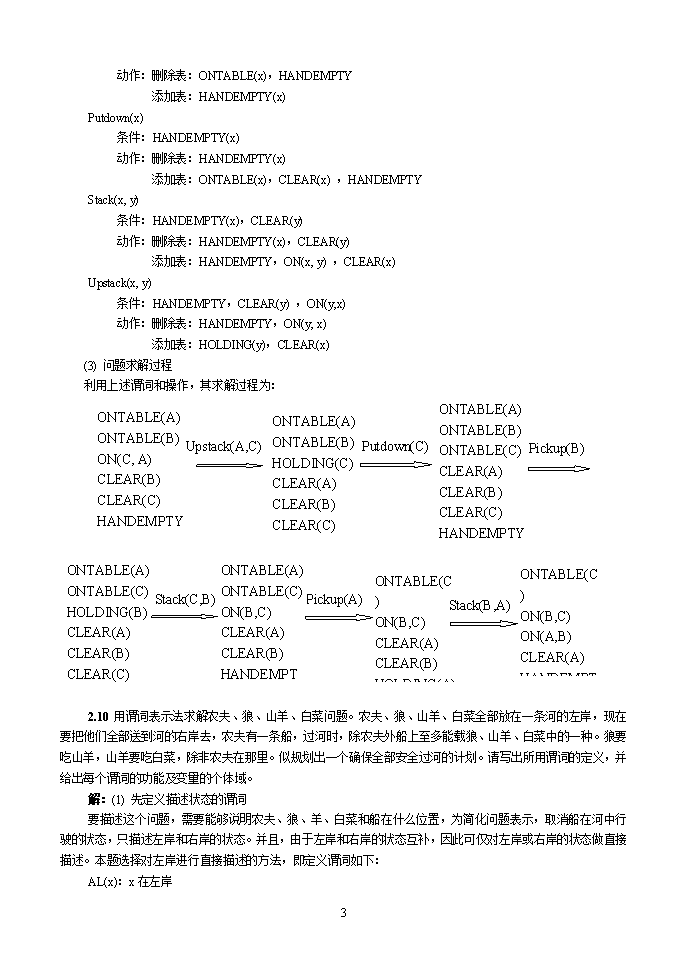解：定义谓词P(x)：x是人L(x,y)：x喜欢y将知识用谓词表示为：(x)(P(x)∧L(x,pragramming)→L(x,computer))35 2.9用谓词表示法求解机器人摞积木问题。设机器人有一只机械手，要处理的世界有一张桌子，桌上可堆放若干相同的方积木块。机械手有4个操作积木的典型动作：从桌上拣起一块积木；将手中的积木放到桌之上；在积木上再摞上一块积木；从积木上面拣起一块积木。积木世界的布局如下图所示。ABCCAB图机器人摞积木问题解：(1)先定义描述状态的谓词CLEAR(x)：积木x上面是空的。ON(x,y)：积木x在积木y的上面。ONTABLE(x)：积木x在桌子上。HOLDING(x)：机械手抓住x。HANDEMPTY：机械手是空的。其中，x和y的个体域都是{A,B,C}。问题的初始状态是：ONTABLE(A)ONTABLE(B)ON(C,A)CLEAR(B)CLEAR(C)HANDEMPTY问题的目标状态是：ONTABLE(C)ON(B,C)ON(A,B)CLEAR(A)HANDEMPTY(2)再定义描述操作的谓词在本问题中，机械手的操作需要定义以下4个谓词：Pickup(x)：从桌面上拣起一块积木x。Putdown(x)：将手中的积木放到桌面上。Stack(x,y)：在积木x上面再摞上一块积木y。Upstack(x,y)：从积木x上面拣起一块积木y。其中，每一个操作都可分为条件和动作两部分，具体描述如下：Pickup(x)条件：ONTABLE(x)，HANDEMPTY，CLEAR(x)35 动作：删除表：ONTABLE(x)，HANDEMPTY添加表：HANDEMPTY(x)Putdown(x)条件：HANDEMPTY(x)动作：删除表：HANDEMPTY(x)添加表：ONTABLE(x)，CLEAR(x)，HANDEMPTYStack(x,y)条件：HANDEMPTY(x)，CLEAR(y)动作：删除表：HANDEMPTY(x)，CLEAR(y)添加表：HANDEMPTY，ON(x,y)，CLEAR(x)Upstack(x,y)条件：HANDEMPTY，CLEAR(y)，ON(y,x)动作：删除表：HANDEMPTY，ON(y,x)添加表：HOLDING(y)，CLEAR(x)(3)问题求解过程利用上述谓词和操作，其求解过程为：ONTABLE(A)ONTABLE(B)ONTABLE(C)CLEAR(A)CLEAR(B)CLEAR(C)HANDEMPTYONTABLE(A)ONTABLE(B)ON(C,A)CLEAR(B)CLEAR(C)HANDEMPTYONTABLE(A)ONTABLE(B)HOLDING(C)CLEAR(A)CLEAR(B)CLEAR(C)Upstack(A,C)Putdown(C)Pickup(B)ONTABLE(A)ONTABLE(C)ON(B,C)CLEAR(A)CLEAR(B)HANDEMPTYONTABLE(A)ONTABLE(C)HOLDING(B)CLEAR(A)CLEAR(B)CLEAR(C)ONTABLE(C)ON(B,C)ON(A,B)CLEAR(A)HANDEMPTONTABLE(C)ON(B,C)CLEAR(A)CLEAR(B)HOLDING(A)Stack(B,A)Stack(C,B)Pickup(A)2.10用谓词表示法求解农夫、狼、山羊、白菜问题。农夫、狼、山羊、白菜全部放在一条河的左岸，现在要把他们全部送到河的右岸去，农夫有一条船，过河时，除农夫外船上至多能载狼、山羊、白菜中的一种。狼要吃山羊，山羊要吃白菜，除非农夫在那里。似规划出一个确保全部安全过河的计划。请写出所用谓词的定义，并给出每个谓词的功能及变量的个体域。解：(1)先定义描述状态的谓词要描述这个问题，需要能够说明农夫、狼、羊、白菜和船在什么位置，为简化问题表示，取消船在河中行驶的状态，只描述左岸和右岸的状态。并且，由于左岸和右岸的状态互补，因此可仅对左岸或右岸的状态做直接描述。本题选择对左岸进行直接描述的方法，即定义谓词如下：AL(x)：x在左岸35 其中，x的个体域是{农夫，船，狼，羊，白菜}。对应地，¬AL(x)表示x在右岸。问题的初始状态：AL(农夫)AL(船)AL(狼)AL(羊)AL(白菜)问题的目标状态：¬AL(农夫)¬AL(船)¬AL(狼)¬AL(羊)¬AL(白菜)(2)再定义描述操作的谓词本题需要以下4个描述操作的谓词：L-R：农夫自己划船从左岸到右岸L-R(x)：农夫带着x划船从左岸到右岸R-L：农夫自己划船从右岸到左岸R-L(x)：农夫带着x划船从右岸到左岸其中，x的个体域是{狼，羊，白菜}。对上述每个操作，都包括条件和动作两部分。它们对应的条件和动作如下：L-R：农夫划船从左岸到右岸条件：AL(船)，AL(农夫)，¬AL(狼)∨¬AL(羊)，¬AL(羊)∨¬AL(白菜)动作：删除表：AL(船)，AL(农夫)添加表：¬AL(船)，¬AL(农夫)L-R(狼)：农夫带着狼划船从左岸到右岸条件：AL(船)，AL(农夫)，AL(狼)，¬AL(羊)动作：删除表：AL(船)，AL(农夫)，AL(狼)添加表：¬AL(船)，¬AL(农夫)，¬AL(狼)L-R(羊)：农夫带着羊划船从左岸到右岸条件：AL(船)，AL(农夫)，AL(羊)，AL(狼)，AL(白菜)或：AL(船)，AL(农夫)，AL(羊)，¬AL(狼)，¬AL(白菜)动作：删除表：AL(船)，AL(农夫)，AL(羊)添加表：¬AL(船)，¬AL(农夫)，¬AL(羊)L-R(白菜)：农夫带着白菜划船从左岸到右岸条件：AL(船)，AL(农夫)，AL(白菜)，¬AL(狼)动作：删除表：AL(船)，AL(农夫)，AL(白菜)添加表：¬AL(船)，¬AL(农夫)，¬AL(白菜)R-L：农夫划船从右岸到左岸条件：¬AL(船)，¬AL(农夫)，AL(狼)∨AL(羊)，AL(羊)∨AL(白菜)35 或：¬AL(船)，¬AL(农夫)，¬AL(狼)，¬AL(白菜)，AL(羊)动作：删除表：¬AL(船)，¬AL(农夫)添加表：AL(船)，AL(农夫)R-L(羊)：农夫带着羊划船从右岸到左岸条件：¬AL(船)，¬AL(农夫)，¬AL(羊)，¬AL(狼)，¬AL(羊)，AL(白菜)动作：删除表：¬AL(船)，¬AL(农夫)，¬AL(羊)添加表：AL(船)，AL(农夫)，AL(羊)(3)问题求解过程AL(白菜)¬AL(农夫)¬AL(船)¬AL(狼)¬AL(羊)AL(农夫)AL(船)AL(狼)AL(白菜)¬AL(羊)AL(狼)AL(白菜)¬AL(农夫)¬AL(船)¬AL(羊)AL(农夫)R-LR-L(羊)L-R(狼)L-R(羊)AL(船)AL(狼)AL(羊)AL(白菜)AL(农夫)AL(船)AL(羊)AL(白菜)¬AL(狼)AL(农夫)AL(船)AL(羊)¬AL(白菜)¬AL(狼)AL(羊)¬AL(农夫)¬AL(船)¬AL(白菜)¬AL(狼)L-R(羊)¬AL(农夫)¬AL(船)¬AL(羊)¬AL(白菜)¬AL(狼)R-LL-R(白菜)2.11用谓词表示法求解修道士和野人问题。在河的北岸有三个修道士、三个野人和一条船，修道士们想用这条船将所有的人都运过河去，但要受到以下条件限制：(1)修道士和野人都会划船，但船一次只能装运两个人。(2)在任何岸边，野人数不能超过修道士，否则修道士会被野人吃掉。假定野人愿意服从任何一种过河安排，请规划出一种确保修道士安全的过河方案。要求写出所用谓词的定义、功能及变量的个体域。解：（1）定义谓词先定义修道士和野人人数关系的谓词：G(x,y,S)：在状态S下x大于yGE(x,y,S)：在状态S下x大于或等于y其中，x,y分别代表修道士人数和野人数，他们的个体域均为{0,1,2,3}。再定义船所在岸的谓词和修道士不在该岸上的谓词：Boat(z,S)：状态S下船在z岸EZ(x,S)：状态S下x等于0，即修道士不在该岸上其中，z的个体域是{L,R}，L表示左岸，R表示右岸。再定义安全性谓词：Safety(z,x,y,S)≡(G(x,0,S)∧GE(x,y,S))∨(EZ(x,S))其中，z,x,y的含义同上。该谓词的含义是：状态S下，在z岸，保证修道士安全，当且仅当修道士不在该岸上，或者修道士在该岸上，但人数超过野人数。该谓词同时也描述了相应的状态。再定义描述过河方案的谓词：L-R(x,x1,y,y1,S)：x1个修道士和y1个野人渡船从河的左岸到河的右岸35 条件：Safety(L,x-x1,y-y1,S’)∧Safety(R,3-x+x1,3-y+y1,S’)∧Boat(L,S)动作：Safety(L,x-x1,y-y1,S’)∧Safety(R,3-x+x1,3-y+y1,S’)∧Boat(R,S’)R-L(x,x1,y,y1,S)：x2个修道士和y2个野人渡船从河的左岸到河的右岸条件：Safety(R,3-x-x2,3-y-y2,S’)∧Safety(L,x+x2,y+y2,S’)∧Boat(R,S)动作：Safety(R,3-x-x2,3-y-y2,S’)∧Safety(L,x+x2,y+y2,S’)∧Boat(L,S’)(2)过河方案Safety(L,3,3,S0)∧Safety(R,0,0,S0)∧Boat(L,S0)L-R(3,1,3,1,S0)L-R(3,0,3,2,S0)Safety(L,2,2,S1)∧Safety(R,1,1,S1)∧Boat(R,S1)Safety(L,3,1,S1’)∧Safety(R,0,2,S1’)∧Boat(R,S1’)R-L(2,1,2,0,S1)R-L(3,0,1,1,S1’)Safety(L,3,2,S2)∧Safety(R,0,1,S2)∧Boat(L,S2)L-R(3,0,2,2,S2)Safety(L,3,0,S3)∧Safety(R,0,3,S3)∧Boat(R,S3)R-L(3,0,0,1,S3)Safety(L,3,1,S4)∧Safety(R,0,2,S1)∧Boat(L,S4)L-R(3,2,1,0,S4)Safety(L,1,1,S5)∧Safety(R,2,2,S5)∧Boat(R,S5)R-L(1,1,1,1,S5)Safety(L,2,2,S6)∧Safety(R,1,1,S6)∧Boat(L,S6)L-R(2,2,2,0,S6)Safety(L,0,2,S7)∧Safety(R,3,1,S7)∧Boat(R,S7)R-L(0,0,2,1,S7)Safety(L,0,3,S8)∧Safety(R,3,0,S8)∧Boat(L,S8)L-R(0,0,3,2,S8)Safety(L,0,1,S9)∧Safety(R,3,2,S9)∧Boat(R,S9)R-L(0,1,1,0,S9)Safety(L,1,1,S10)∧Safety(R,2,2,S10)∧Boat(L,S10)L-R(1,1,1,1,S10)Safety(L,0,0,S11)∧Safety(R,3,3,S11)∧Boat(R,S11)2.18请对下列命题分别写出它们的语义网络：(1)每个学生都有一台计算机。gGSgGSGS解：占有权计算机学生AKOISAISAFOwnsOwnercosg35 (2)高老师从3月到7月给计算机系学生讲《计算机网络》课。解：7月8月StartEnd老师ISAObjectSubject高老师计算机系学生讲课事件ActionCaurse计算机网络讲课(3)学习班的学员有男、有女、有研究生、有本科生。解：参例2.14(4)创新公司在科海大街56号，刘洋是该公司的经理，他32岁、硕士学位。解：参例2.10(5)红队与蓝队进行足球比赛，最后以3：2的比分结束。解：比赛AKOParticipants1Outcome3:22足球赛红队Participants2蓝队2.19请把下列命题用一个语义网络表示出来：(1)树和草都是植物；植物解：AKOAKO草树(2)树和草都有叶和根；根叶解：HaveHave植物是一种是一种草树35 (3)水草是草，且生长在水中；解：LiveAKOAKO水草水中植物草(4)果树是树，且会结果；解：CanAKOAKO果树结果植物树(5)梨树是果树中的一种，它会结梨。解：CanAKOAKO梨树树果树结梨2.25假设有以下一段天气预报：“北京地区今天白天晴，偏北风3级，最高气温12º，最低气温-2º，降水概率15%。”请用框架表示这一知识。解：Frame<天气预报>地域：北京时段：今天白天天气：晴风向：偏北风力：3级气温：最高：12度最低：-2度降水概率：15%2.26按“师生框架”、“教师框架”、“学生框架”的形式写出一个框架系统的描述。解：师生框架FrameName：Unit（Last-name，First-name）Sex：Area（male，female）Default：maleAge：Unit（Years）Telephone：HomeUnit（Number）MobileUnit（Number）35 教师框架FrameAKOMajor：Unit（Major-Name）Lectures：Unit（Course-Name）Field：Unit（Field-Name）Project：Area（National，Provincial，Other）Default：ProvincialPaper：Area（SCI，EI，Core，General）Default：Core学生框架FrameAKOMajor：Unit（Major-Name）Classes：Unit（Classes-Name）Degree：Area（doctor，mastor,bachelor）Default：bachelor第3章确定性推理部分参考答案3.8判断下列公式是否为可合一，若可合一，则求出其最一般合一。(1)P(a,b),P(x,y)(2)P(f(x),b),P(y,z)(3)P(f(x),y),P(y,f(b))(4)P(f(y),y,x),P(x,f(a),f(b))(5)P(x,y),P(y,x)解：(1)可合一，其最一般和一为：σ={a/x,b/y}。(2)可合一，其最一般和一为：σ={y/f(x),b/z}。(3)可合一，其最一般和一为：σ={f(b)/y,b/x}。(4)不可合一。(5)可合一，其最一般和一为：σ={y/x}。3.11把下列谓词公式化成子句集：(1)(x)(y)(P(x,y)∧Q(x,y))(2)(x)(y)(P(x,y)→Q(x,y))(3)(x)(y)(P(x,y)∨(Q(x,y)→R(x,y)))(4)(x)(y)(z)(P(x,y)→Q(x,y)∨R(x,z))解：(1)由于(x)(y)(P(x,y)∧Q(x,y))已经是Skolem标准型，且P(x,y)∧Q(x,y)35 已经是合取范式，所以可直接消去全称量词、合取词，得{P(x,y),Q(x,y)}再进行变元换名得子句集：S={P(x,y),Q(u,v)}(2)对谓词公式(x)(y)(P(x,y)→Q(x,y))，先消去连接词“→”得：(x)(y)(¬P(x,y)∨Q(x,y))此公式已为Skolem标准型。再消去全称量词得子句集：S={¬P(x,y)∨Q(x,y)}(3)对谓词公式(x)(y)(P(x,y)∨(Q(x,y)→R(x,y)))，先消去连接词“→”得：(x)(y)(P(x,y)∨(¬Q(x,y)∨R(x,y)))此公式已为前束范式。再消去存在量词，即用Skolem函数f(x)替换y得：(x)(P(x,f(x))∨¬Q(x,f(x))∨R(x,f(x)))此公式已为Skolem标准型。最后消去全称量词得子句集：S={P(x,f(x))∨¬Q(x,f(x))∨R(x,f(x))}(4)对谓词(x)(y)(z)(P(x,y)→Q(x,y)∨R(x,z))，先消去连接词“→”得：(x)(y)(z)(¬P(x,y)∨Q(x,y)∨R(x,z))再消去存在量词，即用Skolem函数f(x)替换y得：(x)(y)(¬P(x,y)∨Q(x,y)∨R(x,f(x,y)))此公式已为Skolem标准型。最后消去全称量词得子句集：S={¬P(x,y)∨Q(x,y)∨R(x,f(x,y))}3-13判断下列子句集中哪些是不可满足的：(1){¬P∨Q,¬Q,P,¬P}(2){P∨Q,¬P∨Q,P∨¬Q,¬P∨¬Q}(3){P(y)∨Q(y),¬P(f(x))∨R(a)}(4){¬P(x)∨Q(x),¬P(y)∨R(y),P(a),S(a),¬S(z)∨¬R(z)}(5){¬P(x)∨Q(f(x),a),¬P(h(y))∨Q(f(h(y)),a)∨¬P(z)}(6){P(x)∨Q(x)∨R(x),¬P(y)∨R(y),¬Q(a),¬R(b)}解：(1)不可满足，其归结过程为：¬P∨Q¬Q¬PPNIL35 P∨Q¬P∨QQP∨¬Q¬P∨¬Q¬QNIL(2)不可满足，其归结过程为：(3)不是不可满足的，原因是不能由它导出空子句。(4)不可满足，其归结过程略(5)不是不可满足的，原因是不能由它导出空子句。(6)不可满足，其归结过程略3.14对下列各题分别证明G是否为F1,F2,…,Fn的逻辑结论：(1)F:(x)(y)(P(x,y)G:(y)(x)(P(x,y)(2)F:(x)(P(x)∧(Q(a)∨Q(b)))G:(x)(P(x)∧Q(x))(3)F:(x)(y)(P(f(x))∧(Q(f(y)))G:P(f(a))∧P(y)∧Q(y)(4)F1:(x)(P(x)→(y)(Q(y)→L(x.y)))F2:(x)(P(x)∧(y)(R(y)→L(x.y)))G:(x)(R(x)→Q(x))(5)F1:(x)(P(x)→(Q(x)∧R(x)))F2:(x)(P(x)∧S(x))G:(x)(S(x)∧R(x))解：(1)先将F和¬G化成子句集：S={P(a,b),¬P(x,b)}再对S进行归结：¬P(x,b)P(a,b)NIL{a/x}所以，G是F的逻辑结论(2)先将F和¬G化成子句集由F得：S1={P(x)，(Q(a)∨Q(b))}由于¬G为：¬(x)(P(x)∧Q(x))，即(x)(¬P(x)∨¬Q(x))，可得：S2={¬P(x)∨¬Q(x)}因此，扩充的子句集为：S={P(x)，(Q(a)∨Q(b))，¬P(x)∨¬Q(x)}再对S进行归结：Q(a)∨Q(b){a/b}¬P(x)∨¬Q(x)Q(a)35 {a/x}¬P(a)P(x){a/x}NIL所以，G是F的逻辑结论同理可求得(3)、(4)和(5)，其求解过程略。3.15设已知：(1)如果x是y的父亲，y是z的父亲，则x是z的祖父；(2)每个人都有一个父亲。使用归结演绎推理证明：对于某人u，一定存在一个人v，v是u的祖父。解：先定义谓词F(x,y)：x是y的父亲GF(x,z)：x是z的祖父P(x)：x是一个人再用谓词把问题描述出来：已知F1：(x)(y)(z)(F(x,y)∧F(y,z))→GF(x,z))F2：(y)(P(x)→F(x,y))求证结论G：(u)(v)(P(u)→GF(v,u))然后再将F1，F2和¬G化成子句集：①¬F(x,y)∨¬F(y,z)∨GF(x,z)②¬P(r)∨F(s,r)③P(u)④¬GF(v,u))对上述扩充的子句集，其归结推理过程如下：¬F(x,y)∨¬F(y,z)∨GF(x,z)¬GF(v,u)¬F(x,y)∨¬F(y,z)¬P(r)∨F(s,r)¬F(y,z)∨¬P(y)¬P(r)∨F(s,r)¬P(y)∨¬P(z)¬P(y)P(u)NIL{x/v,z/u}{x/s,y/r}{y/s,z/r}{y/z}35 {y/u}由于导出了空子句，故结论得证。3.16假设张被盗，公安局派出5个人去调查。案情分析时，贞察员A说：“赵与钱中至少有一个人作案”，贞察员B说：“钱与孙中至少有一个人作案”，贞察员C说：“孙与李中至少有一个人作案”，贞察员D说：“赵与孙中至少有一个人与此案无关”，贞察员E说：“钱与李中至少有一个人与此案无关”。如果这5个侦察员的话都是可信的，使用归结演绎推理求出谁是盗窃犯。解：(1)先定义谓词和常量设C(x)表示x作案，Z表示赵，Q表示钱，S表示孙，L表示李(2)将已知事实用谓词公式表示出来赵与钱中至少有一个人作案：C(Z)∨C(Q)钱与孙中至少有一个人作案：C(Q)∨C(S)孙与李中至少有一个人作案：C(S)∨C(L)赵与孙中至少有一个人与此案无关：¬(C(Z)∧C(S))，即¬C(Z)∨¬C(S)钱与李中至少有一个人与此案无关：¬(C(Q)∧C(L))，即¬C(Q)∨¬C(L)(3)将所要求的问题用谓词公式表示出来，并与其否定取析取。设作案者为u，则要求的结论是C(u)。将其与其否)取析取，得：¬C(u)∨C(u)(4)对上述扩充的子句集，按归结原理进行归结，其修改的证明树如下：C(Z)∨C(Q)¬C(Z)∨¬C(S)C(Q)∨¬C(S)C(Q)∨C(S)C(Q)¬C(u)∨C(u)C(Q){Q/u}因此，钱是盗窃犯。实际上，本案的盗窃犯不止一人。根据归结原理还可以得出：C(S)∨C(L)¬C(Q)∨¬C(L)C(S)∨¬C(Q)C(Q)∨C(S)C(S)¬C(u)∨C(u)C(S)¬C(Q)∨¬C(L)C(S)∨C(L)C(Q)∨C(S)C(S)∨¬C(Q)¬C(u)∨C(u)C(S)35 {S/u}C(S)因此，孙也是盗窃犯。3.18设有子句集：{P(x)∨Q(a,b),P(a)∨Q(a,b),Q(a,f(a)),P(x)∨Q(x,b)}分别用各种归结策略求出其归结式。解：支持集策略不可用，原因是没有指明哪个子句是由目标公式的否定化简来的。删除策略不可用，原因是子句集中没有没有重言式和具有包孕关系的子句。单文字子句策略的归结过程如下：Q(a,f(a))P(x)∨Q(a,b){b/f(a)}P(x)∨Q(x,b)P(a)Q(a,f(a))Q(a,b){a/x}{b/f(a)}Q(a,b)用线性输入策略（同时满足祖先过滤策略）的归结过程如下：P(a)∨Q(a,b)P(x)∨Q(a,b)P(x)∨Q(x,b)P(a){a/x}{a/x}Q(a,f(a))Q(a,b){b/f(a)}NIL3.19设已知：(1)能阅读的人是识字的；(2)海豚不识字；(3)有些海豚是很聪明的。请用归结演绎推理证明：有些很聪明的人并不识字。解：第一步，先定义谓词，设R(x)表示x是能阅读的；35 K(y)表示y是识字的；W(z)表示z是很聪明的；第二步，将已知事实和目标用谓词公式表示出来能阅读的人是识字的：(x)(R(x))→K(x))海豚不识字：(y)(¬K(y))有些海豚是很聪明的：(z)W(z)有些很聪明的人并不识字：(x)(W(z)∧¬K(x))第三步，将上述已知事实和目标的否定化成子句集：¬R(x))∨K(x)¬K(y)W(z)¬W(z)∨K(x))第四步，用归结演绎推理进行证明W(z)¬W(z)∨K(x))W(z)K(z)NIL3.20对子句集：{P∨Q,Q∨R,R∨W,R∨P,W∨Q,Q∨R}用线性输入策略是否可证明该子句集的不可满足性？解：用线性输入策略不能证明子句集{P∨Q,Q∨R,R∨W,R∨P,W∨Q,Q∨R}的不可满足性。原因是按线性输入策略，不存在从该子句集到空子句地归结过程。3.21对线性输入策略和单文字子句策略分别给出一个反例，以说明它们是不完备的。3.22分别说明正向、逆向、双向与/或形演绎推理的基本思想。3.23设已知事实为((P∨Q)∧R)∨(S∧(T∨U))F规则为S→(X∧Y)∨Z试用正向演绎推理推出所有可能的子目标。解：先给出已知事实的与/或树，再利用F规则进行推理，其规则演绎系统如下图所示。由该图可以直接写出所有可能的目标子句如下：P∨Q∨Ｔ∨Ｕ35 　　P∨Q∨Ｘ∨Ｚ　　P∨Q∨Y∨ＺR∨T∨UR∨X∨ZR∨Y∨Z所有子目标UTZYXRQP所有目标UTZYXRQPYXZX∧YSUTT∨US所有目标UTZYXRQP所有目标YZUTXPRQYXXYF规则ZX∧YX∧YZSSUTQPTUQP已知事实已知事实T∨USR(P∨Q)T∨URS(P∨Q)(S∧(T∨U))((P∨Q)∧R)(S∧(T∨U))((P∨Q)∧R)((P∨Q)∧R)∨(S∧(T∨U))((P∨Q)∧R)∨(S∧(T∨U))3.24设有如下一段知识：“张、王和李都属于高山协会。该协会的每个成员不是滑雪运动员，就是登山运动员，其中不喜欢雨的运动员是登山运动员，不喜欢雪的运动员不是滑雪运动员。王不喜欢张所喜欢的一切东西，而喜欢张所不喜欢的一切东西。张喜欢雨和雪。”试用谓词公式集合表示这段知识，这些谓词公式要适合一个逆向的基于规则的演绎系统。试说明这样一个系统怎样才能回答问题：“高山俱乐部中有没有一个成员，他是一个登山运动员，但不是一个滑雪运动员？”解：(1)先定义谓词A(x)表示x是高山协会会员S(x)表示x是滑雪运动员C(x)表示x是登山运动员L(x,y)表示x喜欢y35 (2)将问题用谓词表示出来“张、王和李都属于高山协会A(Zhang)∧A(Wang)∧A(Li)高山协会的每个成员不是滑雪运动员，就是登山运动员(x)(A(x)∧¬S(x)→C(x))高山协会中不喜欢雨的运动员是登山运动员(x)(¬L(x,Rain)→C(x))高山协会中不喜欢雪的运动员不是滑雪运动员(x)(¬L(x,Snow)→¬S(x))王不喜欢张所喜欢的一切东西(y)(L(Zhang,y)→¬L(Wang,y))王喜欢张所不喜欢的一切东西(y)(¬L(Zhang,y)→L(Wang,y))张喜欢雨和雪L(Zhang,Rain)∧L(Zhang,Snow)(3)将问题要求的答案用谓词表示出来高山俱乐部中有没有一个成员，他是一个登山运动员，但不是一个滑雪运动员？(x)(A(x)→C(x)∧¬S(x))(4)为了进行推理，把问题划分为已知事实和规则两大部分。假设，划分如下：已知事实：A(Zhang)∧A(Wang)∧A(Li)L(Zhang,Rain)∧L(Zhang,Snow)规则：(x)(A(x)∧¬S(x)→C(x))(x)(¬L(x,Rain)→C(x))(x)(¬L(x,Snow)→¬S(x))(y)(L(Zhang,y)→¬L(Wang,y))(y)(¬L(Zhang,y)→L(Wang,y))(5)把已知事实、规则和目标化成推理所需要的形式事实已经是文字的合取形式：f1:A(Zhang)∧A(Wang)∧A(Li)f2:L(Zhang,Rain)∧L(Zhang,Snow)将规则转化为后件为单文字的形式：r1:A(x)∧¬S(x)→C(x))r2:¬L(x,Rain)→C(x)r3:¬L(x,Snow)→¬S(x)r4:L(Zhang,y)→¬L(Wang,y)r5:¬L(Zhang,y)→L(Wang,y)将目标公式转换为与/或形式¬A(x)∨(C(x)∧¬S(x))35 (6)进行逆向推理逆向推理的关键是要能够推出L(Zhang,Rain)∧L(Zhang,Snow)，其逆向演绎过程如下图所示。¬A(x)∨(C(x)∧¬S(x))C(x)∧¬S(x)¬A(x)C(x)¬S(x)r2r34¬L(x,Rain)¬L(x,Snow){Wang/x,y/Rain}{Wang/x,y/Snow}¬L(Wang,y)¬L(Wang,y)r4r4L(Zhang,y)L(Zhang,y){Rain/y}{Snow/y}L(Zhang,Snow)L(Zhang,Rain)第4章搜索策略部分参考答案4.5有一农夫带一条狼，一只羊和一框青菜与从河的左岸乘船倒右岸，但受到下列条件的限制：(1)船太小，农夫每次只能带一样东西过河；(2)如果没有农夫看管，则狼要吃羊，羊要吃菜。请设计一个过河方案，使得农夫、浪、羊都能不受损失的过河，画出相应的状态空间图。题示：(1)用四元组（农夫，狼，羊，菜）表示状态，其中每个元素都为0或1，用0表示在左岸，用1表示在右岸。(2)把每次过河的一种安排作为一种操作，每次过河都必须有农夫，因为只有他可以划船。解：第一步，定义问题的描述形式用四元组S=（f，w，s，v）表示问题状态，其中，f，w，s和v分别表示农夫，狼，羊和青菜是否在左岸，它们都可以取1或0，取1表示在左岸，取0表示在右岸。第二步，用所定义的问题状态表示方式，把所有可能的问题状态表示出来，包括问题的初始状态和目标状态。由于状态变量有4个，每个状态变量都有2种取值，因此有以下16种可能的状态：S0=(1,1,1,1)，S1=(1,1,1,0)，S2=(1,1,0,1)，S3=(1,1,0,0)S4=(1,0,1,1)，S5=(1,0,1,0)，S6=(1,0,0,1)，S7=(1,0,0,0)S8=(0,1,1,1)，S9=(0,1,1,0)，S10=(0,1,0,1)，S11=(0,1,0,0)S12=(0,0,1,1)，S13=(0,0,1,0)，S14=(0,0,0,1)，S15=(0,0,0,0)35 其中，状态S3，S6，S7，S8，S9，S12是不合法状态，S0和S15分别是初始状态和目标状态。第三步，定义操作，即用于状态变换的算符组F由于每次过河船上都必须有农夫，且除农夫外船上只能载狼，羊和菜中的一种，故算符定义如下：L(i)表示农夫从左岸将第i样东西送到右岸（i=1表示狼，i=2表示羊，i=3表示菜，i=0表示船上除农夫外不载任何东西）。由于农夫必须在船上，故对农夫的表示省略。R(i)表示农夫从右岸将第i样东西带到左岸（i=1表示狼，i=2表示羊，i=3表示菜，i=0表示船上除农夫外不载任何东西）。同样，对农夫的表示省略。这样，所定义的算符组F可以有以下8种算符：L(0)，L(1)，L(2)，L(3)R(0)，R(1)，R(2)，R(3)第四步，根据上述定义的状态和操作进行求解。该问题求解过程的状态空间图如下：(1,1,l,1)L(2)(0,1,0,1)R(0)(1,1,0,1)L(3)L(1)(0,1,0,0)(0,0,0,1)R(2)R(2)(1,1,1,0)(1,0,1,1)L(2)L(3)(0,0,1,0)R(0)(1,0,1,0)L(2)(0,0,0,0)4.7圆盘问题。设有大小不等的三个圆盘A、B、C套在一根轴上，每个盘上都标有数字1、2、3、4，并且每个圆盘都可以独立的绕轴做逆时针转动，每次转动90°，其初始状态S0和目标状态Sg如图4-31所示，请用广度优先搜索和深度优先搜索，求出从S0到Sg的路径。35 CC12222222BAAB42234131231331414443初始状态S0目标状态Sg图431圆盘问题解：设用qA，qB和qC分别表示把A盘，B盘和C盘绕轴逆时针转动90º，这些操作（算符）的排列顺序是qA，qB，qC。应用广度优先搜索，可得到如下搜索树。在该搜索树中，重复出现的状态不再划出，节点旁边的标识Si，i=0,1,2,…，为按节点被扩展的顺序给出的该节点的状态标识。由该图可以看出，从初始状态S0到目标状态Sg的路径是S0→2→5→13(Sg)35 3221113334444233132314122344323141212434233114242413ABCqAqBqC331311224244qA322441311324qBqC413412332334123331313124422412344123412313324112244qC334213112244qA314241231234qB132314242413qC4.7题的广度优先搜索树S0S1S2S4S5S6S7S8S9S10S11S12即SgS3其深度优先搜索略。4.8图4-32是5个城市的交通图，城市之间的连线旁边的数字是城市之间路程的费用。要求从A城出发，经过其它各城市一次且仅一次，最后回到A城，请找出一条最优线路。A10B289C1163128D9E432交通费用图解：这个问题又称为旅行商问题（travellingsalesmanproblem,TSP）或货郎担问题，是一个较有普遍性的实际应用问题。根据数学理论，对n个城市的旅行商问题，其封闭路径的排列总数为：(n!)/n=(n-1)!其计算量相当大。例如，当n=20时，要穷举其所有路径，即使用一个每秒一亿次的计算机来算也需要350年的时间。因此，对这类问题只能用搜索的方法来解决。下图是对图4-32按最小代价搜索所得到的搜索树，树中的节点为城市名称，节点边上的数字为该节点的代价g。其计算公式为g(ni+1)=g(ni)+c(ni,ni+1)35 其中，c(ni,ni+1)为节点ni到ni+1节点的边代价。0A119210102119BDCE98693128386128201917CDB181221ECB10105EDB16E2218DC331288923123868868969126129883C32B222925DC2020EBB16D191622DE31E25C9838E12912BD272426CB2720C1417BE2524DC2621DE6812666E3133E9328D31B926B26E831B28DD27323E35ED27D32C34B302820E28CB21030A30A图4.32的最小代价搜索树可以看出，其最短路经是A-C-D-E-B-A或A-B-E-D-C-A其实，它们是同一条路经。4.11设有如下结构的移动将牌游戏：BBWWE其中，B表示黑色将牌，W表是白色将牌，E表示空格。游戏的规定走法是：(1)任意一个将牌可移入相邻的空格，规定其代价为1；(2)任何一个将牌可相隔1个其它的将牌跳入空格，其代价为跳过将牌的数目加1。游戏要达到的目标什是把所有W都移到B的左边。对这个问题，请定义一个启发函数h(n)，并给出用这个启发函数产生的搜索树。你能否判别这个启发函数是否满足下解要求？再求出的搜索树中，对所有节点是否满足单调限制？解：设h(x)=每个W左边的B的个数，f(x)=d(x)+3*h(x)，其搜索树如下f(x)=0+12=12BBWWEf(x)=1+12=13BBEWWf(x)=1+12=13BBWEWf(x)=2+12=14f(x)=2+9=11BBEWWBEWBWf(x)=3+9=1235 EBWBWf(x)=4+6=10WBEBWf(x)=5+3=8WBWBEf(x)=6+3=9WBWEBf(x)=7+0=7WBWEB4.14设有如图4-34的与/或/树，请分别按和代价法及最大代价法求解树的代价。ABCDt2t3t4t1图4.34习题4.14的与/或树56217223E解：若按和代价法，则该解树的代价为：h(A)=2+3+2+5+2+1+6=21若按最大代价法，则该解树的代价为：h(A)=max{h(B)+5,h(C)+6}=max{(h(E)+2)+5,h(C)+6}=max{(max(2,3)+2)+5,max(2,1)+6}=max((5+5,2+6)=104.15设有如图4-35所示的博弈树，其中最下面的数字是假设的估值，请对该博弈树作如下工作：(1)计算各节点的倒推值；(2)利用α-β剪枝技术剪去不必要的分枝。35 图4.35习题4.15的博弈树305-336-2354-3068-3369S0ABCDEFGHIJKLNM解：各节点的倒推值和剪枝情况如下图所示：习题4.15的倒推值和剪枝情况305-336-2354-3068-336≤0≥0≤0≤-39≤3≥3≤4≥4≤4≥4≤-3≤6≥6S0ABCDEFGHIJKMNL第5章计算智能部分参考答案5.15对遗传法的选择操作：设种群规模为4，个体采用二进制编码，适应度函数为f(x)=x2，初始种群情况如下表所示：编号个体串x适应值百分比累计百分比选中次数S01101010S0201004S03110012S0401117若规定选择概率为100%,选择算法为轮盘赌算法，且依次生成的4个随机数为0.42,0.16,0.89,35 0.71，请填写上表中的全部内容，并求出经本次选择操作后所得到的新的种群。解：表格的完整内容为：编号个体串x适应值百分比累计百分比选中次数S0110101010032.3632.361S0201004165.1837.540S0311001214444.6084.142S04011174915.861001本次选择后所得到的新的种群为：S01=1100S02=1010S03=0111S04=11005.18设某小组有5个同学，分别为S1,S2,S3,S4,S5。若对每个同学的“学习好”程度打分：S1:95S2:85S3:80S4:70S5:90这样就确定了一个模糊集F，它表示该小组同学对“学习好”这一模糊概念的隶属程度，请写出该模糊集。解：对模糊集为F，可表示为：F=95/S1+85/S2+80/S3+70/S4+90/S5或F={95/S1,85/S2,80/S3,70/S4,90/S5}5.19设有论域U={u1,u2,u3,u4,u5}并设F、G是U上的两个模糊集，且有F=0.9/u1+0.7/u2+0.5/u3+0.3/u4G=0.6/u3+0.8/u4+1/u5请分别计算F∩G，F∪G，﹁F。解：F∩G=(0.9∧0)/u1+(0.7∧0)/u2+(0.5∧0.6)/u3+(0.3∧0.8)/u4+(0∧1)/u5=0/u1+0/u2+0.5/u3+0.3/u4+0/u5=0.5/u3+0.3/u4F∪G=(0.9∨0)/u1+(0.7∨0)/u2+(0.5∨0.6)/u3+(0.3∨0.8)/u4+(0∨1)/u5=0.9/u1+0.7/u2+0.6/u3+0.8/u4+1/u5﹁F=(1-0.9)/u1+(1-0.7)/u2+(1-0.5)/u3+(1-0.3)/u4+(1-0)/u5=0.1/u1+0.3/u2+0.5/u3+0.7/u4+1/u55.21设有如下两个模糊关系：请写出R1与R2的合成R1οR2。解：R(1,1)=(0.3∧0.2)∨(0.7∧0.6)∨(0.2∧0.9)=0.2∨0.6∨0.2=0.6R(1,2)=(0.3∧0.8)∨(0.7∧0.4)∨(0.2∧0.1)=0.3∨0.4∨0.1=0.4R(2,1)=(1∧0.2)∨(0∧0.6)∨(0.4∧0.9)=0.2∨0∨0.4=0.4R(2,2)=(1∧0.8)∨(0∧0.4)∨(0.4∧0.1)=0.8∨0∨0.1=0.835 R(3,1)=(0∧0.2)∨(0.5∧0.6)∨(1∧0.9)=0.2∨0.6∨0.9=0.9R(3,2)=(0∧0.8)∨(0.5∧0.4)∨(1∧0.1)=0∨0.4∨0.1=0.4因此有5.22设F是论域U上的模糊集，R是U×V上的模糊关系，F和R分别为：求模糊变换FοR。解：={0.1∨0.4∨0.6,0.3∨0.6∨0.3,0.4∨0.6∨0}={0.6,0.6,0.6}第6章不确定性推理部分参考答案6.8设有如下一组推理规则:r1:IFE1THENE2(0.6)r2:IFE2ANDE3THENE4(0.7)r3:IFE4THENH(0.8)r4:IFE5THENH(0.9)且已知CF(E1)=0.5,CF(E3)=0.6,CF(E5)=0.7。求CF(H)=?解：(1)先由r1求CF(E2)CF(E2)=0.6×max{0,CF(E1)}=0.6×max{0,0.5}=0.3(2)再由r2求CF(E4)CF(E4)=0.7×max{0,min{CF(E2),CF(E3)}}=0.7×max{0,min{0.3,0.6}}=0.21(3)再由r3求CF1(H)CF1(H)=0.8×max{0,CF(E4)}=0.8×max{0,0.21)}=0.168(4)再由r4求CF2(H)35 CF2(H)=0.9×max{0,CF(E5)}=0.9×max{0,0.7)}=0.63(5)最后对CF1(H)和CF2(H)进行合成，求出CF(H)CF(H)=CF1(H)+CF2(H)+CF1(H)×CF2(H)=0.6926.10 设有如下推理规则r1:IFE1THEN(2,0.00001)H1r2:IFE2THEN(100,0.0001)H1r3:IFE3THEN(200,0.001)H2r4:IFH1THEN(50,0.1)H2且已知P(E1)=P(E2)=P(H3)=0.6,P(H1)=0.091,P(H2)=0.01,又由用户告知：P(E1|S1)=0.84,P(E2|S2)=0.68,P(E3|S3)=0.36请用主观Bayes方法求P(H2|S1,S2,S3)=?解：(1)由r1计算O(H1|S1)先把H1的先验概率更新为在E1下的后验概率P(H1|E1)P(H1|E1)=(LS1×P(H1))/((LS1-1)×P(H1)+1)=(2×0.091)/((2-1)×0.091+1)=0.16682由于P(E1|S1)=0.84>P(E1)，使用P(H|S)公式的后半部分，得到在当前观察S1下的后验概率P(H1|S1)和后验几率O(H1|S1)P(H1|S1)=P(H1)+((P(H1|E1)–P(H1))/(1-P(E1)))×(P(E1|S1)–P(E1))=0.091+(0.16682–0.091)/(1–0.6))×(0.84–0.6)=0.091+0.18955×0.24=0.136492O(H1|S1)=P(H1|S1)/(1-P(H1|S1))=0.15807(2)由r2计算O(H1|S2)先把H1的先验概率更新为在E2下的后验概率P(H1|E2)P(H1|E2)=(LS2×P(H1))/((LS2-1)×P(H1)+1)=(100×0.091)/((100-1)×0.091+1)=0.90918由于P(E2|S2)=0.68>P(E2)，使用P(H|S)公式的后半部分，得到在当前观察S2下的后验概率P(H1|S2)和后验几率O(H1|S2)P(H1|S2)=P(H1)+((P(H1|E2)–P(H1))/(1-P(E2)))×(P(E2|S2)–P(E2))=0.091+(0.90918–0.091)/(1–0.6))×(0.68–0.6)=0.25464O(H1|S2)=P(H1|S2)/(1-P(H1|S2))=0.34163(3)计算O(H1|S1,S2)和P(H1|S1,S2)先将H1的先验概率转换为先验几率O(H1)=P(H1)/(1-P(H1))=0.091/(1-0.091)=0.1001135 再根据合成公式计算H1的后验几率O(H1|S1,S2)=(O(H1|S1)/O(H1))×(O(H1|S2)/O(H1))×O(H1)=(0.15807/0.10011)×(0.34163)/0.10011)×0.10011=0.53942再将该后验几率转换为后验概率P(H1|S1,S2)=O(H1|S1,S2)/(1+O(H1|S1,S2))=0.35040(4)由r3计算O(H2|S3)先把H2的先验概率更新为在E3下的后验概率P(H2|E3)P(H2|E3)=(LS3×P(H2))/((LS3-1)×P(H2)+1)=(200×0.01)/((200-1)×0.01+1)=0.09569由于P(E3|S3)=0.36P(H1)，使用P(H|S)公式的后半部分，得到在当前观察S1,S2下H2的后验概率P(H2|S1,S2)和后验几率O(H2|S1,S2)P(H2|S1,S2)=P(H2)+((P(H2|H1)–P(H2))/(1-P(H1)))×(P(H1|S1,S2)–P(H1))=0.01+(0.33557–0.01)/(1–0.091))×(0.35040–0.091)=0.10291O(H2|S1,S2)=P(H2|S1,S2)/(1-P(H2|S1,S2))=0.10291/(1-0.10291)=0.11472(6)计算O(H2|S1,S2,S3)和P(H2|S1,S2,S3)先将H2的先验概率转换为先验几率O(H2)=P(H2)/(1-P(H2))=0.01/(1-0.01)=0.0101035 再根据合成公式计算H1的后验几率O(H2|S1,S2,S3)=(O(H2|S1,S2)/O(H2))×(O(H2|S3)/O(H2))×O(H2)=(0.11472/0.01010)×(0.00604)/0.01010)×0.01010=0.06832再将该后验几率转换为后验概率P(H2|S1,S2,S3)=O(H1|S1,S2,S3)/(1+O(H1|S1,S2,S3))=0.06832/(1+0.06832)=0.06395可见，H2原来的概率是0.01，经过上述推理后得到的后验概率是0.06395，它相当于先验概率的6倍多。6.11设有如下推理规则r1:IFE1THEN(100,0.1)H1r2:IFE2THEN(50,0.5)H2r3:IFE3THEN(5,0.05)H3且已知P(H1)=0.02,P(H2)=0.2,P(H3)=0.4，请计算当证据E1，E2，E3存在或不存在时P(Hi|Ei)或P(Hi|﹁Ei)的值各是多少(i=1,2,3)？解：(1)当E1、E2、E3肯定存在时，根据r1、r2、r3有P(H1|E1)=(LS1×P(H1))/((LS1-1)×P(H1)+1)=(100×0.02)/((100-1)×0.02+1)=0.671P(H2|E2)=(LS2×P(H2))/((LS2-1)×P(H2)+1)=(50×0.2)/((50-1)×0.2+1)=0.9921P(H3|E3)=(LS3×P(H3))/((LS3-1)×P(H3)+1)=(5×0.4)/((5-1)×0.4+1)=0.769(2)当E1、E2、E3肯定存在时，根据r1、r2、r3有P(H1|¬E1)=(LN1×P(H1))/((LN1-1)×P(H1)+1)=(0.1×0.02)/((0.1-1)×0.02+1)=0.002P(H2|¬E2)=(LN2×P(H2))/((LN2-1)×P(H2)+1)=(0.5×0.2)/((0.5-1)×0.2+1)=0.111P(H3|¬E3)=(LN3×P(H3))/((LN3-1)×P(H3)+1)=(0.05×0.4)/((0.05-1)×0.4+1)=0.0326.13设有如下一组推理规则:r1:IFE1ANDE2THENA={a}(CF={0.9})r2:IFE2AND(E3ORE4)THENB={b1,b2}(CF={0.8,0.7})r3:IFATHENH={h1,h2,h3}(CF={0.6,0.5,0.4})35 r4:IFBTHENH={h1,h2,h3}(CF={0.3,0.2,0.1})且已知初始证据的确定性分别为：CER(E1)=0.6,CER(E2)=0.7,CER(E3)=0.8,CER(E4)=0.9。假设|Ω|=10，求CER(H)。解：其推理过程参考例6.9具体过程略6.15设U=V={1，2，3，4}且有如下推理规则：IFxis少THENyis多其中，“少”与“多”分别是U与V上的模糊集，设少=0.9/1+0.7/2+0.4/3多=0.3/2+0.7/3+0.9/4已知事实为xis较少“较少”的模糊集为较少=0.8/1+0.5/2+0.2/3请用模糊关系Rm求出模糊结论。解：先用模糊关系Rm求出规则IFxis少THENyis多所包含的模糊关系RmRm(1,1)=(0.9∧0)∨(1-0.9)=0.1Rm(1,2)=(0.9∧0.3)∨(1-0.9)=0.3Rm(1,3)=(0.9∧0.7)∨(1-0.9)=0.7Rm(1,4)=(0.9∧0.9)∨(1-0.9)=0.7Rm(2,1)=(0.7∧0)∨(1-0.7)=0.3Rm(2,2)=(0.7∧0.3)∨(1-0.7)=0.3Rm(2,3)=(0.7∧0.7)∨(1-0.7)=0.7Rm(2,4)=(0.7∧0.9)∨(1-0.7)=0.7Rm(3,1)=(0.4∧0)∨(1-0.4)=0.6Rm(3,2)=(0.4∧0.3)∨(1-0.4)=0.6Rm(3,3)=(0.4∧0.7)∨(1-0.4)=0.6Rm(3,4)=(0.4∧0.9)∨(1-0.4)=0.6Rm(4,1)=(0∧0)∨(1-0)=1Rm(4,2)=(0∧0.3)∨(1-0)=1Rm(4,3)=(0∧0.7)∨(1-0)=1Rm(3,4)=(0∧0.9)∨(1-0)=1即：35 因此有即，模糊结论为Y’={0.3,0.3,0.7,0.8}6.16设U=V=W={1,2,3,4}且设有如下规则：r1：IFxisFTHENyisGr2：IFyisGTHENzisHr3：IFxisFTHENzisH其中，F、G、H的模糊集分别为：F=1/1+0.8/2+0.5/3+0.4/4G=0.1/2+0.2/3+0.4/4H=0.2/2+0.5/3+0.8/4请分别对各种模糊关系验证满足模糊三段论的情况。解：本题的解题思路是：由模糊集F和G求出r1所表示的模糊关系R1m,R1c,R1g再由模糊集G和H求出r2所表示的模糊关系R2m,R2c,R2g再由模糊集F和H求出r3所表示的模糊关系R3m,R3c,R3g然后再将R1m,R1c,R1g分别与R2m,R2c,R2g合成得R12m,R12c,R12g最后将R12m,R12c,R12g分别与R3m,R3c,R3g比较第7章机器学习参考答案7-6设训练例子集如下表所示：序号属性分类x1x21TT+35 2TT+3TF-4FF+5FT_6FT_请用ID3算法完成其学习过程。解：设根节点为S，尽管它包含了所有的训练例子，但却没有包含任何分类信息，因此具有最大的信息熵。即：H(S)=-(P(+)log2P(+)+P(-)log2P(-))式中P(+)=3/6，P(-)=3/6分别是决策方案为“+”或“-”时的概率。因此有H(S)=-((3/6)log2(3/6)+(3/6)log2(3/6))=1按照ID3算法，需要选择一个能使S的期望熵为最小的一个属性对根节点进行扩展，因此我们需要先计算S关于每个属性的条件熵：H(S|xi)=(|ST|/|S|)*H(ST)+(|SF|/|S|)*H(SF)其中，T和F为属性xi的属性值，ST和SF分别为xi=T或xi=F时的例子集，|S|、|ST|和|SF|分别为例子集S、ST和SF的大小。下面先计算S关于属性x1的条件熵：在本题中，当x1=T时，有：ST={1，2，3}当x1=F时，有：SF={4，5，6}其中，ST和SF中的数字均为例子集S中的各个例子的序号，且有|S|=6，|ST|=|SF|=3。由ST可知，其决策方案为“+”或“-”的概率分别是：　　　　PST(+)=2/3PST(-)=1/3因此有：H(ST)=-(PST(+)log2PST(+)+PST(-)log2PST(-))=-((2/3)log2(2/3)+(1/3)log2(1/3))=0.9183再由SF可知，其决策方案为“+”或“-”的概率分别是：　　　　PSF(+)=1/3PSF(-)=2/3则有：H(SF)=-(PSF(+)log2PSF(+)+PSF(-)log2PSF(-))=-((1/3)log2(1/3)+(2/3)log2(2/3))=0.918335 将H(ST)和H(SF)代入条件熵公式，有：H(S|x1)=(|ST|/|S|)H(ST)+(|SF|/|S|)H(SF)=(3/6)﹡0.9183+(3/6)﹡0.9183=0.9183下面再计算S关于属性x2的条件熵：在本题中，当x2=T时，有：ST={1，2，5，6}当x2=F时，有：SF={3，4}其中，ST和SF中的数字均为例子集S中的各个例子的序号，且有|S|=6，|ST|=4，|SF|=2。由ST可知：　　　　PST(+)=2/4PST(-)=2/4则有：H(ST)=-(PST(+)log2PST(+)+PST(-)log2PST(-))=-((2/4)log2(2/4)+(2/4)log2(2/4))=1再由SF可知：　　　　PSF(+)=1/2PSF(-)=1/2则有：H(SF)=-(P(+)log2P(+)+P(-)log2P(-))=-((1/2)log2(1/2)+(1/2)log2(1/2))=1将H(ST)和H(SF)代入条件熵公式，有：H(S|x2)=(|ST|/|S|)H(ST)+(|SF|/|S|)H(SF)=(4/6)﹡1+(2/6)﹡1=1可见，应该选择属性x1对根节点进行扩展。用x1对S扩展后所得到的部分决策树如下图所示。S(+,+,-)(+,-,-)x1=Tx1=F扩展x1后的部分决策树在该决策树中，其2个叶节点均不是最终决策方案，因此还需要继续扩展。而要继续扩展，只有属性x2可选择，因此不需要再进行条件熵的计算，可直接对属性x2进行扩展。对x2扩展后所得到的决策树如下图所示：35 S(+,+,-)(+,-,-)x1=Tx2=F扩展x2后得到的完整决策树(+,+)(-)(-,-)(+)x2=Tx2=Fx2=Tx2=F7-9假设w1(0)=0.2,w2(0)=0.4,θ(0)=0.3,η=0.4，请用单层感知器完成逻辑或运算的学习过程。解：根据“或”运算的逻辑关系，可将问题转换为：输入向量：X1=[0,0,1,1]X2=[0,1,0,1]输出向量：Y=[0,1,1,1]由题意可知，初始连接权值、阈值，以及增益因子的取值分别为：w1(0)=0.2,w2(0)=0.4,θ(0)=0.3，η=0.4即其输入向量X(0)和连接权值向量W(0)可分别表示为：X(0)=(-1,x1(0),x2(0))W(0)=(θ(0),w1(0),w2(0))根据单层感知起学习算法，其学习过程如下：设感知器的两个输入为x1(0)=0和x2(0)=0，其期望输出为d(0)=0，实际输出为：y(0)=f(w1(0)x1(0)+w2(0)x2(0)-θ(0))=f(0.2*0+0.4*0-0.3)=f(-0.3)=0实际输出与期望输出相同，不需要调节权值。再取下一组输入：x1(0)=0和x2(0)=1，其期望输出为d(0)=1，实际输出为：y(0)=f(w1(0)x1(0)+w2(0)x2(0)-θ(0))=f(0.2*0+0.4*1-0.3)=f(0.1)=1实际输出与期望输出相同，不需要调节权值。再取下一组输入：x1(0)=1和x2(0)=0，其期望输出为d(0)=1，实际输出为：y(0)=f(w1(0)x1(0)+w2(0)x2(0)-θ(0))=f(0.2*1+0.4*0-0.3)=f(-0.1)=0实际输出与期望输出不同，需要调节权值，其调整如下：θ(1)=θ(0)+η(d(0)-y(0))*(-1)=0.3+0.4*(1-0)*(-1)=-0.1w1(1)=w1(0)+η(d(0)-y(0))x1(0)=0.2+0.4*(1-0)*1=0.6w2(1)=w2(0)+η(d(0)-y(0))x2(0)=0.4+0.4*(1-0)*0=0.4再取下一组输入：x1(1)=1和x2(1)=1，其期望输出为d(1)=1，实际输出为：y(1)=f(w1(1)x1(1)+w2(1)x2(1)-θ(1))=f(0.6*1+0.4*1+0.1)=f(1.1)=135 实际输出与期望输出相同，不需要调节权值。再取下一组输入：x1(1)=0和x2(1)=0，其期望输出为d(0)=0，实际输出为：y(1)=f(w1(1)x1(1)+w2(1)x2(1)-θ(1))=f(0.6*0+0.4*0+0.1)=f(0.1)=1实际输出与期望输出不同，需要调节权值，其调整如下：θ(2)=θ(1)+η(d(1)-y(1))*(-1)=-0.1+0.4*(0-1)*(-1)=0.3w1(2)=w1(1)+η(d(1)-y(1))x1(1)=0.6+0.4*(0-1)*0=0.6w2(2)=w2(1)+η(d(1)-y(1))x2(1)=0.4+0.4*(0-1)*0=0.4再取下一组输入：x1(2)=0和x2(2)=1，其期望输出为d(2)=1，实际输出为：y(2)=f(w1(2)x1(2)+w2(2)x2(2)-θ(2))=f(0.6*0+0.4*1-0.3)=f(0.1)=1实际输出与期望输出相同，不需要调节权值。再取下一组输入：x1(2)=1和x2(2)=0，其期望输出为d(2)=1，实际输出为：y(2)=f(w1(2)x1(2)+w2(2)x2(2)-θ(2))=f(0.6*1+0.4*0-0.3)=f(0.3)=1实际输出与期望输出相同，不需要调节权值。再取下一组输入：x1(2)=1和x2(2)=1，其期望输出为d(2)=1，实际输出为：y(2)=f(w1(2)x1(2)+w2(2)x2(2)-θ(2))=f(0.6*1+0.4*1-0.3)=f(0.7)=1实际输出与期望输出相同，不需要调节权值。至此，学习过程结束。最后的得到的阈值和连接权值分别为：θ(2)=0.3w1(2)=0.6w2(2)=0.4不仿验证如下：对输入：“00”有y=f(0.6*0+0.4*0-0.3)=f(-0.3)=0对输入：“01”有y=f(0.6*0+0.4*1-0.3)=f(0.1)=1对输入：“10”有y=f(0.6*1+0.4*0-0.3)=f(0.3)=1对输入：“11”有y=f(0.6*1+0.4*1-0.3)=f(0.7)=135'