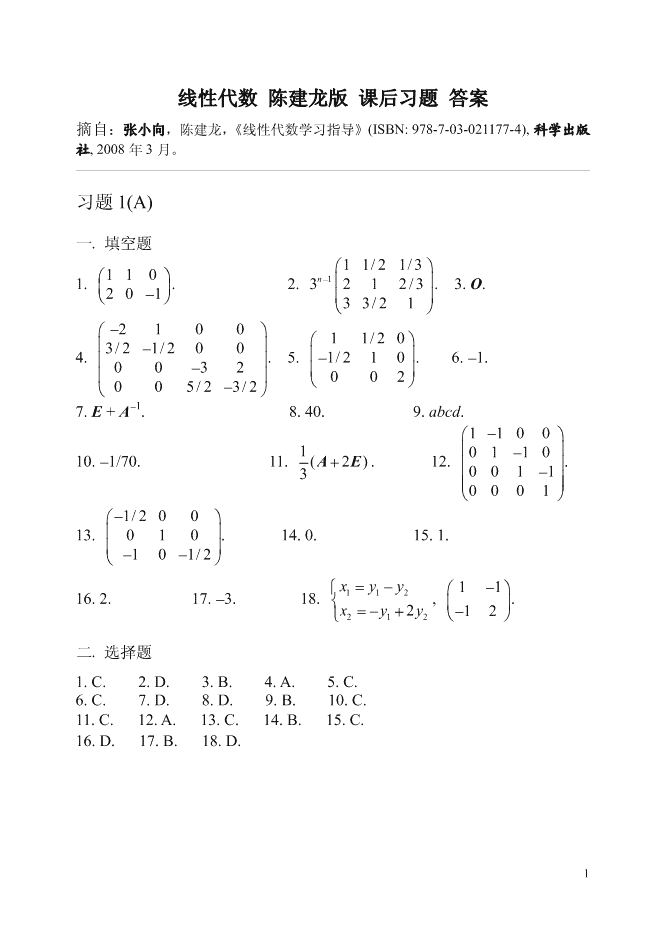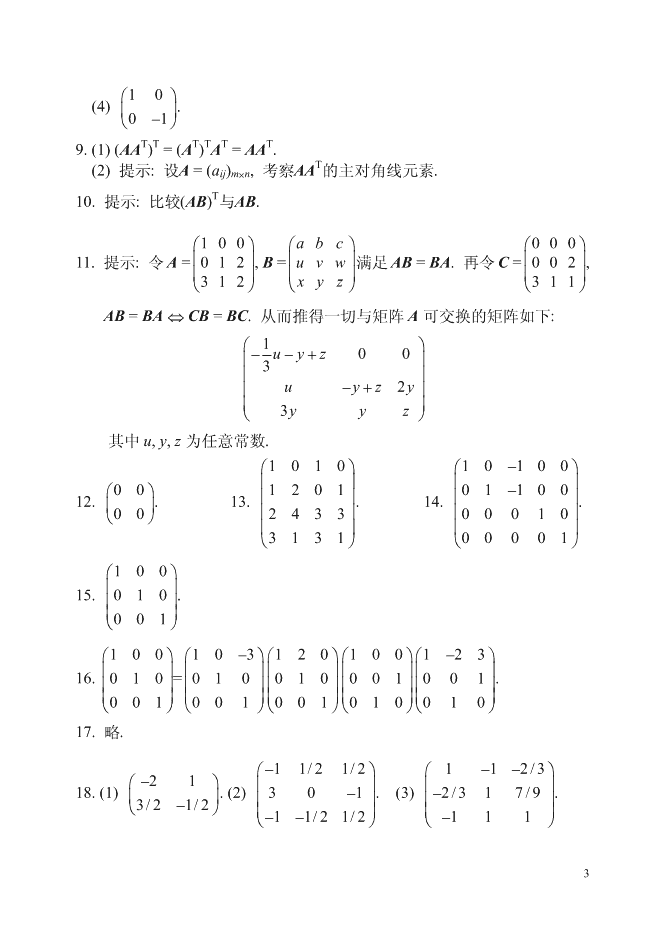线性代数 (陈建龙 著) 科学出版社 课后答案.pdf 24页

'线性代数陈建龙版课后习题答案摘自：张小向，陈建龙，《线性代数学习指导》(ISBN:978-7-03-021177-4),科学出版社,2008年3月。习题1(A)一.填空题⎛⎞11/21/31.⎛110⎞.2.3212n−1⎜⎟/3.3.O.⎜⎟⎝⎠201−⎜⎟⎝⎠33/21⎛⎞−2100⎛⎞11/20⎜⎟3/2−1/2004.⎜⎟.5.⎜⎟−1/210.6.−1.0032−⎜⎟⎜⎟⎝⎠002⎝⎠005/23−/2−17.E+A.8.40.9.abcd.⎛⎞1100−1⎜⎟0110−10.−1/70.11.(2A+E).12.⎜⎟.30011−⎜⎟⎜⎟⎝⎠0001⎛⎞−1/20013.⎜010⎟.14.0.15.1.⎜⎟⎝⎠−−101/2⎧xyy112=−⎛⎞11−16.2.17.−3.18.⎨,⎜⎟.⎩x=−+yy2⎝⎠−12212二.选择题1.C.2.D.3.B.4.A.5.C.6.C.7.D.8.D.9.B.10.C.11.C.12.A.13.C.14.B.15.C.16.D.17.B.18.D.1 习题1(B)⎛⎞6112⎛⎞−21322⎛⎞058⎛1019⎞1.⎜⎟113−,⎜⎟.2.⎜⎟−−21720,⎜⎟056−.⎜⎟⎝⎠1466⎝⎠73⎜⎟⎝⎠4292−⎜⎟⎝⎠290⎧xz=−65−+zz,11239999⎪⎛⎞−23⎛⎞−24ii343.⎨xzzz2123=−+1227,4.4,⎜⎟,⎜⎟10099.⎪⎝⎠−46⎝⎠−46i4⎩x=−10zzz−5+20.3123⎛⎞35⎛⎞da11da12da13⎜⎟⎜⎟5.(1)6.(2)(068).(3)dbdbdb.⎜⎟⎜⎟212223⎜⎟49⎜⎟dcdcdc⎝⎠⎝⎠313233⎛⎞ad11ad22ad33n⎜⎟(4)⎜⎟bd11bd22bd33.(5)∑axxijij.⎜⎟ij,1=cdcdcd⎝⎠112233123⎛⎞010⎛⎞010⎛⎞010⎛⎞001⎛⎞010⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟(6)001=001,001=000,001=O,⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎝⎠000⎜⎟⎝⎠000⎜⎟⎝⎠000⎜⎟⎝⎠000⎜⎟⎝⎠000n⎛⎞010⎜⎟当n>3时,001=O.⎜⎟⎜⎟000⎝⎠⎛⎞nn−−12nn(1−)nn⎛⎞4000λλn2λ⎜⎟⎜⎟0400(7)0λλnnn−1.(8)⎜⎟.⎜⎟⎜⎟0040⎜⎟00λn⎝⎠⎜⎟⎝⎠0004⎛⎞00⎜⎟6.02.7.都不成立⎜⎟⎜⎟12⎝⎠⎛01⎞⎛10⎞⎛10⎞⎛00⎞⎛⎞008.(1)⎜⎟.(2)⎜⎟.(3)A=⎜⎟,X=⎜⎟,Y=⎜⎟.⎝⎠00⎝⎠00⎝⎠00⎝⎠00⎝⎠012 ⎛⎞10(4)⎜⎟.⎝⎠01−TTTTTT9.(1)(AA)=(A)A=AA.T(2)提示:设A=(aij)m×n,考察AA的主对角线元素.T10.提示:比较(AB)与AB.⎛⎞100⎛⎞abc⎛⎞00011.提示:令A=⎜⎟012,B=⎜uvw⎟满足AB=BA.再令C=⎜⎟002,⎜⎟⎜⎟⎜⎟⎝⎠312⎝⎠xyz⎝⎠311AB=BA⇔CB=BC.从而推得一切与矩阵A可交换的矩阵如下:⎛⎞1⎜⎟−−+uyz003⎜⎟⎜⎟uy−+z2y⎜⎟⎝⎠3yyz其中u,y,z为任意常数.⎛⎞1010⎛⎞10100−⎜⎟⎜⎟⎛⎞00120101100−12.⎜⎟.13.⎜⎟.14.⎜⎟.⎝⎠00⎜2433⎟⎜⎟00010⎜⎟⎜⎟⎝⎠3131⎝⎠00001⎛⎞100⎜⎟15.010.⎜⎟⎜⎟001⎝⎠⎛⎞100⎛⎞103−⎛⎞120⎛⎞100⎛⎞123−⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟16.010=010010001001.⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎝⎠001⎜⎟⎝⎠001⎜⎟⎝⎠001⎜⎟⎝⎠010⎜⎟⎝⎠01017.略.⎛⎞−11/21/2⎛⎞112−−/3⎛⎞−21⎜⎟⎜⎟18.(1)⎜⎟.(2)⎜⎟301−.(3)⎜⎟−2/317/9.⎝⎠3/2−1/2⎜⎟⎝⎠−−11/21/2⎜⎟⎝⎠−1113 ⎛⎞210−⎛⎞−51⎛⎞133−/2⎜⎟19.(1)⎜⎟.(2)⎜⎟.(3)⎜⎟134−.⎝⎠30⎝⎠011−⎜⎟⎝⎠102−⎛⎞−21220.⎜⎟.⎝⎠013−−−1−1−1−121.(1)X=EX=(AA)X=A(AX)=A(AY)=(AA)Y=EY=Y.−1−1−1−1(2)X=XE=X(AA)=(XA)A=(YA)A=Y(AA)=YE=Y.T−1T−1TT−1TT−1−122.A(A)=(AA)=E=E⇒(A)=(A)=A.2−1−1−1−1−12−123.A=(PBP)(PBP)=PB(PP)BP=PBEBP=PBP.kk−1依此类推,对于任意的正整数k,A=PBP.n设f(x)=anx+…+a1x+a0,则nn−1−1−1f(A)=anA+…+a1A+a0E=anPBP+…+a1PBP+a0PPn−1−1=P(anB+…+a1B+a0E)P=Pf(B)P.1111−1⎛⎞2731273224.A=PΛP=⎜⎟.⎝⎠−−683684n(n+3)/225.(1)27.(2)160.(3)−29400000.(4)(−1)anan−1"a2a1.nn+1nn−1(5)a+(−1)b.(6)(−1)(n−1).(7)n+1.n1n−2n−1n(8)(a1−∑)a2…an.(9)an+an−1x+…+a2x+a1x+x.i=2ai26.提示:用课本第29页性质1.3(2).3127.a0=3,a1=−,a2=2,a3=−.2228.16,20,0.−1−11−1129.提示:|A||(3A)−2A*|=|A[(3A)−2A*]|=|AA−2AA*|=|E−E|332238=|−E|=(−)=−.3327⎛⎞2955−19⎜⎟30.52317.⎜⎟⎜⎟⎝⎠26210−1−1−131.提示:AA*=|A|E⇒(|A|A)A*=E⇒(A*)=|A|A.4 −1−1−1−1−1−1(A)(A)*=|A|E=|A|E⇒(A)*=|A|A.32.略.⎛⎞53000⎜⎟−−32000⎜⎟33.⎜001/200⎟(提示:用课本第39页定理1.10).⎜⎟⎜⎟00025−⎜⎟⎝⎠00038−32234.提示:A−2A+9A−E=O⇒A(A−2A+9E)=E.322A−2A+9A−E=O⇒(A+9E)(A−2E)=−17E.35.(1)x1=1,x2=1,x3=1,x4=1.ab−abab−−ba−abab−−23n13n(2)x1=ii"i,x2=ii"i,…,aaaaaa−−−aaaaaa−−−2131n12131n1baba−−ba−12n−1xn=ii"i.aaaaaa−−−nn12nn−136.(1)2.(2)3.37.λ=5,µ=1.38.设PA=U,QA=V,其中P为m阶可逆矩阵,Q为s阶可逆矩阵,U,V均为行阶梯行矩阵,则⎛⎞PO⎛⎞AC⎛⎞UPC(1)⎜⎟⎜⎟=⎜⎟,故⎝⎠OQ⎝⎠OB⎝⎠OV⎛⎞AC⎛⎞UPCr⎜⎟=r⎜⎟≥r(U)+r(V)=r(A)+r(B).⎝⎠OB⎝⎠OV⎛⎞PO⎛⎞AO⎛⎞UO(2)⎜⎟⎜⎟=⎜⎟,故⎝⎠OQ⎝⎠OB⎝⎠OV⎛⎞AC⎛⎞UOr⎜⎟=r⎜⎟=r(U)+r(V)=r(A)+r(B).⎝⎠OB⎝⎠OV()r39.提示:(充分性)A,B的等价标准形都是E.(必要性)初等变换不改变mn×矩阵的秩.5 习题2(A)一.填空题T1.(−9,−4,7,−4).2.2.3.5.4.无.5.a=2b.6.相.7.a≠2.⎛⎞0⎛⎞1⎛⎞0⎛⎞0⎛⎞1⎛⎞4⎛⎞0⎛⎞0⎛⎞4⎛⎞1⎛⎞0⎛⎞4⎜⎟2⎜⎟0⎜⎟0⎜⎟2⎜⎟0⎜⎟5⎜⎟2⎜⎟0⎜⎟5⎜⎟0⎜⎟0⎜⎟58.⎜⎟,⎜⎟,⎜⎟;或⎜⎟,⎜⎟,⎜⎟;或⎜⎟,⎜⎟,⎜⎟;或⎜⎟,⎜⎟,⎜⎟.003006036036⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎝⎠0⎝⎠0⎝⎠0⎝⎠0⎝⎠0⎝⎠0⎝⎠0⎝⎠0⎝⎠0⎝⎠0⎝⎠0⎝⎠09.(0,1,0,4),(2,0,0,5),(0,0,3,6).10.(1,0,−1),(0,1,−1).(注:本题答案不唯一)11.(0,1,−1).(注:本题答案不唯一)⎛−1⎞⎛5/31/3⎞12.⎜⎟.13.⎜⎟.14.t+2s=0.⎝⎠3⎝⎠−4/31/3⎛⎞1⎛⎞11115.⎜⎟2,⎜⎟−1.(注:本题答案不唯一)3⎜⎟3⎜⎟⎝⎠2⎝⎠−116.a=−1,b=0,c=0.二.选择题1.C.2.D.3.A.4.C.5.D.6.B.7.D.8.A.9.B.10.D.习题2(B)1.(1)r(α1,α2,α3)=2<3,可见α1,α2,α3是线性相关的.(2)r(α1,α2,α3)=2<3,可见α1,α2,α3是线性相关的.(3)r(α1,α2,α3)=3,可见α1,α2,α3是线性无关的.(4)r(α1,α2,α3)=2<3,可见α1,α2,α3是线性相关的.212.a=.3.a≠0且b≠1/3.4.a=2,b=3.5.略.2⎛⎞1001⎛⎞1001⎜⎟1100⎜⎟11006.提示:(β1,β2,β3,β4)=(α1,α2,α3,α4)⎜⎟,而r⎜⎟<4.01100110⎜⎟⎜⎟⎜⎟⎜⎟⎝⎠0011⎝⎠0011⎛⎞11"1⎛⎞11"1⎜⎟01"1⎜⎟01"17.提示:(β1,β2,…,βs)=(α1,α2,…,αs)⎜⎟,且⎜⎟可逆.##%###%#⎜⎟⎜⎟⎜⎟⎜⎟⎝⎠00"1⎝⎠00"16 ⎛⎞ab08.β1,β2,β3线性无关⇔a≠b.提示:(β1,β2,β3)=(α1,α2,α3)⎜⎟ba0.⎜⎟⎝⎠0ba9.略.10.(方法一)对s使用数学归纳法.参见习题2(C)的第6题.(方法二)因为向量组α1,α2,…,αs线性相关,所以存在一组不全为零的数k1,k2,…,ks使得k1α1+k2α2+…+ksαs=0.设k1,k2,…,ks中最后一个不为零的数是kj,则k1α1+k2α2+…+kj−1αj−1+kjαj=0.k1k2kj−1由此可得αj=−α1−α2−…−αj−1.kkkjjj11.(方法一)因为对于矩阵A=(α1,α2,…,αs)来说,它的每个非零子式所占的列向量构成的向量组的秩就等于这个非零子式的阶数,也就是这个非零子式所占的列向量的个数.因此,A的每个非零子式所占的列向量构成的向量组都是线性无关的.反之,若α1,α2,…,αs的某个线性无关的部分组中含有t个向量,则这个部分组的秩就是t,因而这t列中必然存在一个t阶的非零子式.于是r(α1,α2,…,αs)=r⇔A中存在r阶的非零子式,但任意高于r阶的子式都为零⇔α1,α2,…,αs中存在r个线性无关的向量,但任意多于r个向量的部分组都是线性相关的.(方法二)(⇒)若r(α1,α2,…,αs)=r,则A=(α1,α2,…,αs)中存在r阶的非零子式,但任意高于r阶的子式都为零.因此,①那个r阶的非零子式所占的r列就构成了α1,α2,…,αs的一个线性无关的部分组.②假若α1,α2,…,αs还有t个向量的部分组都是线性无关的,其中t>r,那么这个部分组中必然有一个t阶的非零子式,而这个t阶的非零子式同时也是A的t阶的非零子式.但这与r(α1,α2,…,αs)=r(r,那么这个t阶的非零子式所占的t个列向量的部分组都是线性无关的.但任意多于r个向量的部分组都是线性相关的,矛盾!因此A=(α1,α2,…,αs)中任意高于r阶的子式都为零.综合①和②可知r(α1,α2,…,αs)=r.12.略.13.略.7 14.(⇒)设k1α1+k2α2+…+ksαs=0,η=l1α1+l2α2+…+lsαs,则η=(k1+l1)α1+(k2+l2)α2+…+(ks+ls)αs.由于η由向量组α1,α2,…,αs线性表示的方式是唯一的,所以k1+l1=l1,k2+l2=l2,…,ks+ls=ls.由此可得k1=k2=…=ks=0.故α1,α2,…,αs线性无关.(⇐)设η=l1α1+l2α2+…+lsαs=k1α1+k2α2+…+ksαs,则(k1−l1)α1+(k2−l2)α2+…+(ks−ls)αs=0.由于α1,α2,…,αs是线性无关的,故k1−l1=k2−l2=…=ks−ls=0,即k1=l1,k2=l2,…,ks=ls.可见η由向量组α1,α2,…,αs线性表示的方式是唯一的.15.提示:r(A+B)≤r(A)+r(B),其中A=(α1,α2,…,αs),B=(β1,β2,…,βs).16.见本章典型例题赏析中的例3.⎛⎞a11⎛⎞aaa+++222×1/(a+2)17.当a≠−2时,A=⎜⎟11a×−1→⎜1a1⎟→⎜⎟⎜⎟⎝11a⎠×−1⎝11a⎠⎛⎞111×(1−)⎛⎞111⎜⎟11a←→⎜⎟010a−=B.⎜⎟⎜⎟⎝⎠11a←⎝⎠00a−1⎛⎞a⎛⎞1⎛⎞1若a≠1,则r(A)=r(B)=3,此时向量组⎜⎟1,⎜⎟a,⎜⎟1的极大无关组⎜⎟⎜⎟⎜⎟⎝⎠1⎝⎠1⎝⎠a就是它本身;⎛⎞a⎛⎞a⎛⎞1⎛⎞1若a=1,则r(A)=r(B)=1,此时⎜⎟1就是向量组⎜⎟1,⎜⎟a,⎜⎟1的一⎜⎟⎜⎟⎜⎟⎜⎟⎝⎠1⎝⎠1⎝⎠1⎝⎠a个极大无关组.⎛⎞−211⎛⎞000←当a=−2时,A=⎜⎟121−×1−→⎜⎟121−→⎜⎟⎜⎟⎝112−⎠×1−⎝⎠112−←⎛⎞112−×(1)−⎛⎞112−⎜⎟121−←→⎜033−⎟=C.由此可得r(A)=r(C)=2,且⎜⎟⎜⎟⎝000⎠⎝⎠000⎛⎞a⎛⎞1⎛⎞a⎛⎞1⎛⎞1⎜⎟1,⎜⎟a就是向量组⎜⎟1,⎜⎟a,⎜⎟1的一个极大无关组.⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎝⎠1⎝⎠1⎝⎠1⎝⎠1⎝⎠a8 33318.(1)不构成R的子空间.(2)构成R的子空间.(3)不构成R的子空间.T19.(1)α=(6,3,2)是V的一组基,dimV=1.TT(2)α=(2,1,0),β=(−3,0,1)是V的一组基,dimV=2.(3)α1,α3是V的一组基,dimV=2.(4)α1,α3是V的一组基,dimV=2.20.见本章典型例题赏析中的例5.TTT21.α1=(1,0,2),α2=(0,1,3)是V的一组基.α在这组基下的坐标为(1,1).22.(1)证明略.(2)令A=(α1,α2,α3),从ε1,ε2,ε3到α1,α2,α3的过渡矩阵就是A.⎛⎞−3/21/23/2(3)从α−1=⎜101−⎟.1,α2,α3到ε1,ε2,ε3的过渡矩阵就是A⎜⎟⎝1/2−1/21/2⎠⎛⎞1⎛⎞1(4)η=⎜⎟2在ε1,ε2,ε3下的坐标就是⎜⎟2;在α1,α2,α3下的坐标为⎜⎟⎜⎟⎝⎠3⎝⎠3⎛⎞1⎛⎞4A−1⎜⎟2=⎜−2⎟.⎜⎟⎜⎟⎝⎠3⎝⎠1⎛⎞10123.⎜010⎟.24.⎛⎞1/34/3.⎜⎟⎜⎟⎝⎠4/31/3⎝⎠100TT25.提示:设α=(a1,a2,…,an),β=(b1,b2,…,bn).因为nnnn2222∑ai+2λ∑abii+λ∑bi=∑()abii+λ≥0i=1i=1i=1i=1恒成立,所以nnn222∆=(2∑abii)−4∑ai∑bi≤0.i=1i=1i=1⎛⎞1⎛⎞0⎛⎞−232626.(1)⎜⎟1,⎜⎟1,⎜1⎟.3⎜⎟2⎜⎟6⎜⎟⎝⎠1⎝⎠−1⎝⎠13TT6T(2)(1,0,1,−1),(0,−1,0,0),(1,0,1,2).3627.略.28.略.29.提示:初等矩阵E(i,j)是正交矩阵(1≤i0,YBY>0⎛⎞X⇒对于任意非零的k维列向量Z=⎜⎟(其中X,Y的维数分别为k,l),⎝⎠YTTT⎛AO⎞⎛X⎞TTZMZ=(X,Y)⎜⎟⎜⎟=XAX+YBY>0⎝⎠OB⎝⎠Y⇒M是正定矩阵.(方法二)用特征值.A,B都是正定矩阵⇒A的特征值λ1,…,λk以及B的特征值µ1,…,µl都大于零⎛⎞AO⇒M=⎜⎟的特征值λ1,…,λk,µ1,…,µl都大于零⎝⎠OB⇒M是正定矩阵.(方法三)用标准形.A,B都是正定矩阵TT⇒存在可逆矩阵P,Q使得PAP=Ek,QBQ=El⎛⎞PO⇒存在可逆矩阵⎜⎟,使得⎝⎠OQTT⎛⎞PO⎛⎞AO⎛⎞PO⎛⎞PO⎛⎞AO⎛⎞PO⎜⎟OQ⎜⎟OB⎜⎟OQ=⎜⎟T⎜⎟OB⎜⎟OQ⎝⎠⎝⎠⎝⎠⎝⎠OQ⎝⎠⎝⎠T⎛PAPO⎞⎛EkO⎞=⎜T⎟=⎜⎟=Em⎝⎠OQBQ⎝⎠OEl⇒M是正定矩阵.(方法四)用分解.A,B都是正定矩阵TT⇒存在可逆矩阵P,Q使得A=PP,B=QQ⎛PO⎞⇒存在可逆矩阵⎜⎟,使得⎝⎠OQTT⎛⎞AO⎛⎞PPO⎛⎞PO⎛⎞POM=⎜⎟OB=⎜⎟T=⎜⎟OQ⎜⎟OQ⎝⎠⎝⎠OQQ⎝⎠⎝⎠21 ⇒M是正定矩阵.(方法五)用顺序主子式.A,B都是正定矩阵⇒A,B的各阶顺序主子式都大于零⎛AO⎞⇒M=⎜⎟的各阶顺序主子式都大于零⎝⎠OB(事实上,设∆s是M的s阶顺序主子式,则当s≤k时,∆s也是A的s阶顺序主子式,因而大于零;当s>k时,∆s=|A|∆s−k,其中∆s−k是B的s−k阶顺序主子式,由于|A|和∆s−k都大于零,故∆s大于零)⇒M是正定矩阵.13.提示:考虑特征值.14.提示:若r(A)=n,则对于任意的n维非零列向量ξ,都有Aξ≠0,因而TTTξ(AA)ξ=(Aξ)(Aξ)=||Aξ||>0.15.(必要性)因为A是实对称矩阵,所以存在正交矩阵Q,使得T−1QAQ=QAQ=Λ=diag{λ1,λ2,…,λn},其中n为A的阶数,λ1,λ2,…,λn为A的特征值.T−1因此A=QΛQ=QΛQ.若A是正定的,则λ1,λ2,…,λn全是正数.T−1于是令Ω=diag{λ,λ,…,λ},G=QΩQ=QΩQ,12n则G是正定的,而且TTTTTTTTTGG=(QΩQ)(QΩQ)=[(Q)ΩQ](QΩQ)TTTTT=(QΩQ)(QΩQ)=QΩ(QQ)ΩQ=QΩΩQ2TT=QΩQ=QΛQ=A;2TTTTTG=(QΩQ)(QΩQ)=QΩ(QQ)ΩQ=QΩΩQ2TT=QΩQ=QΛQ=A.(充分性)由于正定阵的行列式大于0,故正定阵一定是可逆的.T若存在正定阵G,使A=GG,则A是正定的.16.提示:设λ为A的一个特征值,即存在非零的向量ξ使得Aξ=λξ.3232于是(λ−4λ+5λ−2)ξ=(A−4A+5A−2E)ξ=Oξ=0.322由此可得λ−4λ+5λ−2=0,即(λ−1)(λ−2)=0,故λ=1或2.17.(法一)设λ为A的一个特征值,即存在非零的向量ξ使得Aξ=λξ..因为A是正定矩阵,所以λ>0.T又因为A是正交矩阵,即AA=E,TTTTT2T所以ξξ=ξ(AA)ξ=(Aξ)(Aξ)=(λξ)(λξ)=λξξ,T2其中ξξ>0.由此可得λ=1,而λ>0,故λ=1.这就是说A的特征值全是1,故存在正交矩阵Q使得22 T−1QAQ=QAQ=E.−1因而A=QEQ=E.T(法二)因为A是正定矩阵,所以A=A,且A的特征值都是正数.2T又因为A是正交矩阵,所以A=AA=E,2因而A的特征值λ必然满足λ=1.综合上述两个方面可知A的特征值全是1,T−1故存在正交矩阵Q使得QAQ=QAQ=E.−1因而A=QEQ=E.TTTTTTTT18.提示:ξBξ=ξ(λE+AA)ξ=ξλEξ+ξAAξ=λξξ+(Aξ)Aξ222=λ||ξ||+||Aξ||≥λ||ξ||.19.−2<λ<1.(提示:考察A的顺序主子式).20.都不是正定的.:⎛⎞b100"⎜⎟0b2"0T21.提示:令C=⎜⎟,则B=(aijbibj)n×n=CAC.##%#⎜⎟⎜⎟00"b⎝⎠n2⎛⎞k00⎜⎟222.Λ=0(2)k+0,k≠0且k≠−2.⎜⎟⎜⎟00(2k+)2⎝⎠⎛⎞000提示:①存在正交矩阵Q使得QTAQ=Q−1AQ=Ω=⎜⎟020.⎜⎟⎝⎠002−1−12222②QBQ=Q(kE+2kA+A)Q=kE+2kΩ+Ω.⎛⎞720−⎛⎞x23.令A=⎜−−262⎟,B=(−6,−24,18),X=⎜⎟y,⎜⎟⎜⎟⎝⎠025−⎝⎠zT则该二次曲面的方程可表示为XAX+BX+18=0.λ−720|λE−A|=26λ−2=(λ−9)(λ−6)(λ−3).02λ−5由此可得A的三个特征值:λ1=9,λ2=6,λ3=3.解(λiE−A)x=0(i=1,2,3)得三个对应的特征向量:TTTξ1=(2,−2,1),ξ2=(−2,−1,2),ξ3=(1,2,2).单位化得:TTTq1=(2/3,−2/3,1/3),q2=(−2/3,−1/3,2/3),q3=(1/3,2/3,2/3),23 ⎛⎞900令Q=(qTT−1⎜⎟1,q2,q3),则QQ=E,QAQ=QAQ=Λ=060,⎜⎟⎝⎠003BQ=(18,24,−6),⎛⎞x′令Y=⎜⎟y′,X=QY,则该二次曲面的方程化为⎜⎟⎝⎠z′TYΛY+BQY+18=0,222即9x′+6y′+3z′+18x′+24y′−6z′+18=0,配方得2229(x′+1)+6(y′+2)+3(z′−1)=18,⎛⎞u⎛⎞x′+1⎛⎞1于是令Z=⎜⎟v=⎜y′+2⎟=Y+⎜2⎟即得该二次曲面的标准方程⎜⎟⎜⎟⎜⎟⎝⎠w⎝⎠z′−1⎝⎠−1222uvw++=1.236⎛⎞1由X=QY和Z=Y+⎜⎟2可得所用的变换公式为⎜⎟⎝⎠−1⎧xuvw=−++2211,333⎪⎨yuvw=−−++2122,333⎪122⎩zuvw=++−1.33311−1⎛⎞224.二次型x2+y2−z2−xy+2xz−2yz的矩阵A=⎜⎟−111−.2⎜⎟⎝⎠111−−λ−111−2|λE−A|=1λ−11=(λ−1)(λ−15+7)(λ−15−7).2244−11λ+1115+715−7由此可得A的三个特征值:λ1=,λ2=,λ3=.244故A的秩为3,正惯性指数为2,负惯性指数为1,因此该二次曲面表示二次锥面.⎛⎞2/3−2/31/3⎛⎞x1⎛⎞y125.Q=⎜−−2/31/32/3⎟.⎜⎟x=Q⎜⎟y,f(x2+2y22−y32.221,x2,x3)=5y1⎜⎟⎜⎟⎜⎟⎝⎠2/32/32/3⎝⎠x3⎝⎠y3f(x1,x2,x3)=5表示单叶双曲面.24'