高中数学必修三《模块综合问题选讲》课后练习(含答案).doc 7页

'www.ks5u.com模块综合问题选讲课后练习题一：一个单位有职工800人，其中具有高级职称的160人，具有中级职称的320人，具有初级职称的200人，其余人员120人．为了解职工收入情况，决定采用分层抽样的方法，从中抽取容量为40的样本．则从上述各层中依次抽取的人数分别是(　　)A．12,24,15,9　　　　　　　B．9,12,12,7C．8,15,12,5D．8,16,10,6题二：某地有居民100000户，其中普通家庭99000户，高收入家庭1000户．从普通家庭中以简单随机抽样方式抽取990户，从高收入家庭中以简单随机抽样方式抽取100户进行调查，发现共有120户家庭拥有3套或3套以上住房，其中普通家庭50户，高收入家庭70户．依据这些数据并结合所掌握的统计知识，你认为该地拥有3套或3套以上住房的家庭所占比例的合理估计是________．题三：一枚硬币连掷3次，有且仅有2次出现正面向上的概率为(　　)A．B．C．D．题四：某商场举行购物抽奖促销活动，规定每位顾客从装有编号为0,1,2,3四个相同小球的抽奖箱中，每次取出一球，记下编号后放回，连续取两次，若取出的两个小球号码相加之和等于6，则中一等奖，等于5中二等奖，等于4或3中三等奖．(1)求中三等奖的概率；(2)求中奖的概率．题五：某篮球运动员在2009赛季各场比赛的得分情况如下：12,15,24,25,31,31,36,36,37,39,44,49,50．制作茎叶图，并分析这个运动员的整体水平及发挥的稳定程度．题六：甲、乙两同学5次综合测评的成绩如茎叶图所示．甲乙9883372109●9老师在计算甲、乙两人平均分时，发现乙同学成绩的一个数字无法看清．若从{0，1，2，…，9}随机取一个数字代替，则乙的平均成绩超过甲的平均成绩的概率为_____．题七：输入－5，按图中所示程序框图运行后，输出的结果是(　　)A．－5　　　　　　B．0C．－1D．1 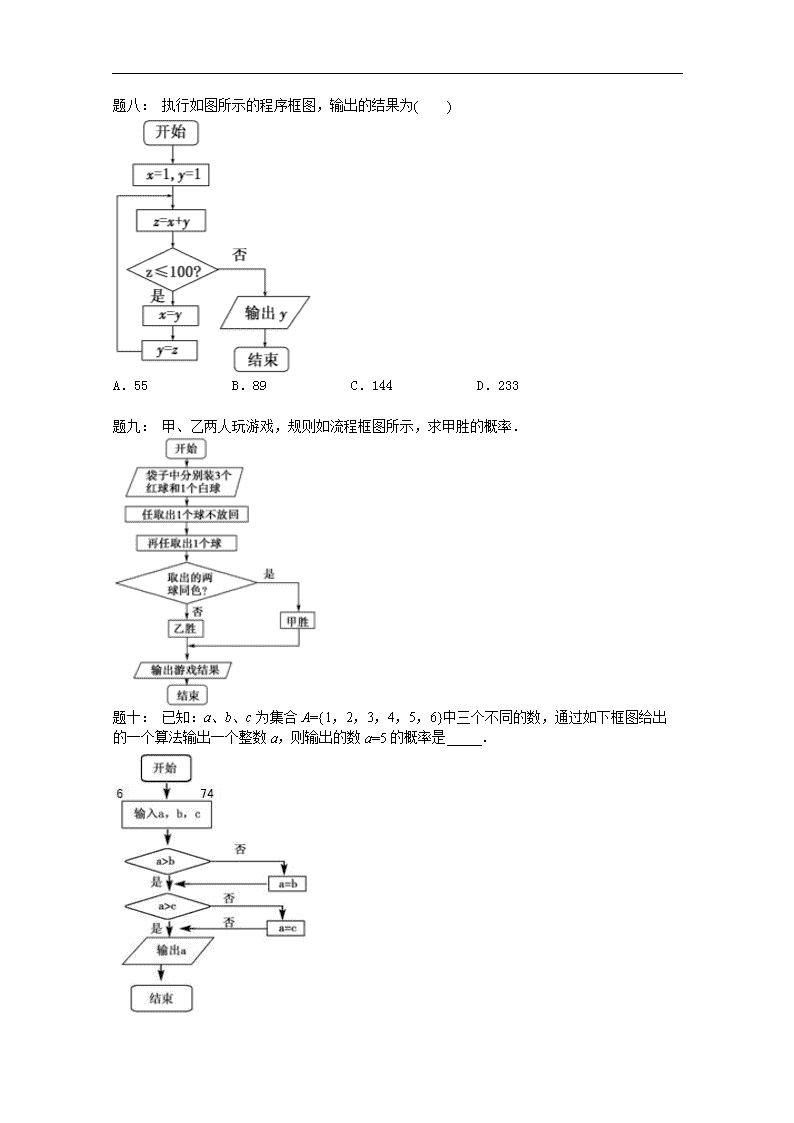题一：执行如图所示的程序框图，输出的结果为(　　)A．55B．89C．144D．233题二：甲、乙两人玩游戏，规则如流程框图所示，求甲胜的概率．题三：已知：a、b、c为集合A={1，2，3，4，5，6}中三个不同的数，通过如下框图给出的一个算法输出一个整数a，则输出的数a=5的概率是_____． 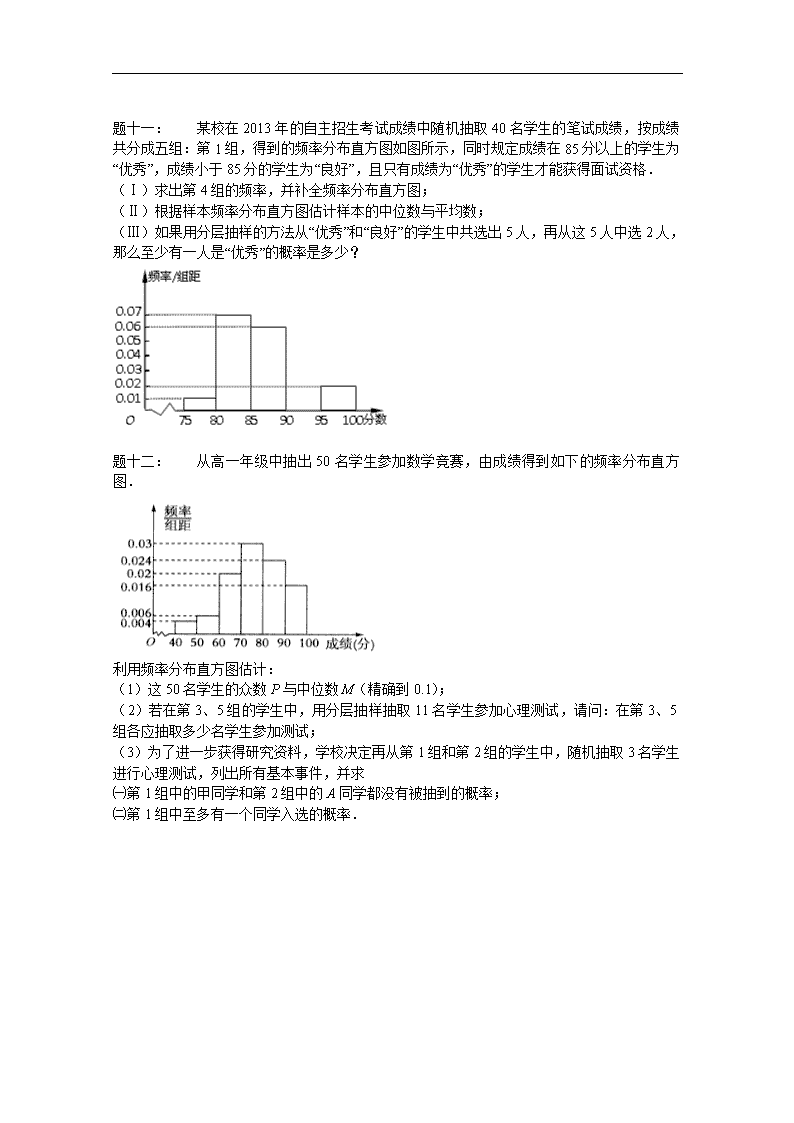题一：某校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩，按成绩共分成五组：第1组，得到的频率分布直方图如图所示，同时规定成绩在85分以上的学生为“优秀”，成绩小于85分的学生为“良好”，且只有成绩为“优秀”的学生才能获得面试资格．（Ⅰ）求出第4组的频率，并补全频率分布直方图；（Ⅱ）根据样本频率分布直方图估计样本的中位数与平均数；（Ⅲ）如果用分层抽样的方法从“优秀”和“良好”的学生中共选出5人，再从这5人中选2人，那么至少有一人是“优秀”的概率是多少？题二：从高一年级中抽出50名学生参加数学竞赛，由成绩得到如下的频率分布直方图．利用频率分布直方图估计：（1）这50名学生的众数P与中位数M（精确到0.1）；（2）若在第3、5组的学生中，用分层抽样抽取11名学生参加心理测试，请问：在第3、5组各应抽取多少名学生参加测试；（3）为了进一步获得研究资料，学校决定再从第1组和第2组的学生中，随机抽取3名学生进行心理测试，列出所有基本事件，并求㈠第1组中的甲同学和第2组中的A同学都没有被抽到的概率；㈡第1组中至多有一个同学入选的概率． 模块综合问题选讲课后练习参考答案题一：D．详解：由题意，各种职称的人数比为160∶320∶200∶120＝4∶8∶5∶3，所以抽取的具有高、中、初级职称的人数和其他人员的人数分别为40×＝8,40×＝16,40×＝10,40×＝6．题二：5.7%详解：普通家庭中拥有3套或3套以上住房的大约为99000×＝5000(户)，　高收入家庭中拥有3套或3套以上住房的大约为1000×＝700(户)．所以，该地拥有3套或3套以上住房的家庭共约有5000＋700＝5700(户)．故＝5.7%．题三：A．详解：所有的基本事件是(正，正，正)，(正，正，反)，(正，反，正)，(正，反，反)，(反，正，正)，(反，正，反)，(反，反，正)，(反，反，反)，共有8个，仅有2次出现正面向上的有：(正，正，反)，(正，反，正)，(反，正，正)，共3个．则所求概率为．题四：(1)；(2)．详解：设“中三等奖”为事件A，“中奖”为事件B，从四个小球中有放回地取两个有(0,0)，(0,1)，(0,2)，(0,3)，(1,0)，(1,1)，(1,2)，(1,3)，(2,0)，(2,1)，(2,2)，(2,3)，(3,0)，(3,1)，(3,2)，(3,3)，共16种不同的结果．(1)取出的两个小球号码相加之和等于4或3的取法有：(1,3)，(2,2)，(3,1)，(0,3)，(1,2)，(2,1)，(3,0)，共7种结果，则中三等奖的概率为P(A)＝．(2)由(1)知两个小球号码相加之和等于3或4的取法有7种；两个小球号码相加之和等于5的取法有2种：(2,3)，(3,2)．两个小球号码相加之和等于6的取法有1种：(3,3)．中奖的概率为P(B)＝＝．题五：见详解．详解：该运动员得分茎叶图如下：图中第一行分界线的左边的“1”表示十位数字，右边的“2”和“5”表示个位数字，这一行说明该运动员的得分为12分和15分．同理，第二行说明得分为24分和25分，第三行说明有两个31分，两个36分，一个37分，一个39分，依此类推． 从这张图中可以粗略地看出，该运动员得分大多都在20分到40分之间，且分布较为对称，集中程度高，说明其发挥比较稳定．题一：．详解：计算甲、乙的平均分，建立不等式，求出满足题意的数字，即可求得概率．甲的平均分为，设●为x，则乙的平均分为，令＞90，则x＞8，即x=9，∴从{0，1，2，…，9}随机取一个数字代替，则乙的平均成绩超过甲的平均成绩的概率为．题二：D．详解：该程序框图执行的是求函数y＝的值的功能，x＝－5时，y＝1．题三：B．详解：初始值：x＝1，y＝1，第1次循环：z＝2，x＝1，y＝2；第2次循环：z＝3，x＝2，y＝3；第3次循环：z＝5，x＝3，y＝5；第4次循环：z＝8，x＝5，y＝8；第5次循环：z＝13，x＝8，y＝13；第6次循环：z＝21，x＝13，y＝21；第7次循环：z＝34，x＝21，y＝34；第8次循环：z＝55，x＝34，y＝55；第9次循环：z＝89，x＝55，y＝89；第10次循环时z＝144，循环结束，输出y，故输出的结果为89．题四：．详解：由题意知“甲胜”意味着两次取出的都是红球，因为袋里有3红1白四个球，把3个红球记为a1，a2，a3，1个白球记为b，两次取球的不同结果有（a1，a2），（a1，a3），（a2，a3），（a2，a1），（a3，a1），（a3，a2），（a1，b），（b，a1），（a2，b），（b，a2），（a3，b），（b，a3）共12种情况，其中两次取出的都是红球的不同结果有：（a1，a2），（a1，a3），（a2，a3），（a2，a1），（a3，a1），（a3，a2）共6种情况，所以甲胜的概率是p=＝．题五：．详解：根据框图判断，本框图输出的a为输入的三个数a，b，c中的最大值最大值是3的情况，输入的三个数为1，2，3  ，共1种情况；最大值是4的情况，输入的三个数为1，2，3里两个以及4 ，共3种情况；最大值是5的情况，输入的三个数为1，2，3，4里两个数以及5  ，共6种情况；最大值是6的情况，输入的三个数为1，2，3，4，5里两个数及6 ，共 10种情况； a=5的概率=．题一：中位数的估计值为，平均数为87.25；0.9．详解：（1）其它组的频率为（0.01+0.07+0.06+0.02）×5=0.8，所以第4组的频率为0.2，频率分布图如图：（2）设样本的中位数为x，则5×0.01+5×0.07+（x-85）×0.06=0.5，解得x=，∴样本中位数的估计值为，平均数为77.5×0.05+82.5×0.35+87.5×0.30+92.5×0.20+97.5×0.10=87.25；（3）依题意良好的人数为40×0.4=16人，优秀的人数为40×0.6=24人优秀与良好的人数比为3：2，所以采用分层抽样的方法抽取的5人中有优秀3人，良好2人，记“从这5人中选2人至少有1人是优秀”为事件M，将考试成绩优秀的三名学生记为A，B，C，考试成绩良好的两名学生记为a，b，从这5人中任选2人的所有基本事件包括：AB，AC，BC，Aa，Ab，Ba，Bb，Ca，Cb，ab共10个基本事件，事件M含的情况是：AB，AC，BC，Aa，Ab，Ba，Bb，Ca，Cb，共9个，所以P（M）==0.9．题二：见详解．详解：思路：（1）由频率分布直方图与众数、中位数的定义求出P=75，M=70；（2）根据第三与第五组的频率，求出第三与第五组的人数，按比例计算可得；（3）先求出第一、第二组的人数，再写出从中抽取3人的所有基本事件，分别找出符合（一），（二）的基本事件，利用古典概型求概率．（1）由频率分布直方图知：众数P=75；中位数M=70，（2）第3组共有学生50×0.02×10=10（人）；第5组共有学生50×0.024×10=12（人）抽取比例为=，∴第3组抽5人；第5组抽6人．（3）第1组共50×0.004×10=2人，用甲、乙表示；第2组共50×0.006×10=3人用A、B、C表示，则从这5名学生中随机抽取3名的所有可能为：（甲，乙，A）（甲，乙，B）（甲，乙，C）（甲，A，B）（甲，A，C）（甲，B，C）（乙，A，B）（乙，A，C）（乙，B，C）（A、B、C）共10个．（一）事件S={第1组中的甲同学和第2组中的A同学都没有被抽到}其有（乙，B，C）共1个，所以P(S)＝． （二）事件T={第1组中至多有一个同学入选}其有（甲，A，B）（甲，A，C）（甲，B，C）（乙，A，B）（乙，A，C）（乙，B，C）（A、B、C）共有7个，所以P(T)＝．'