面向分行轨迹的薄壁件铣削颤振控制方法.pdf 7页

'中国科技论文在线http://www.paper.edu.cn面向分行轨迹的薄壁件铣削颤振控制方法#**周续，张定华，吴宝海，罗明（西北工业大学现代设计与集成制造技术教育部重点实验室，陕西西安710072）5摘要：本文以航空发动机机匣为对象，研究了其铣削过程中的颤振稳定性控制问题。建立了颤振稳定性极限的频域预测方法，在单个切削行内和不同切削行间分析了机匣铣削过程中稳定性叶瓣图的分布情况，并针对不同切削行间稳定性叶瓣图呈现的交错排列现象，难以在整个铣削过程进行切削参数优选，提出了面向分行刀位轨迹的切削参数优选方法，保证了机匣整个材料切除过程的稳定铣削。10关键词：颤振；薄壁件；航空发动机机匣；切削参数优选中图分类号：TP391.7Achattercontrolmethodbasedonsingle-linetoolpathfor15themillingofthin-walledpartsZHOUXu,ZHANGDinghua,WUBaohai,LUOMing(KeyLaboratoryofContemporaryDesignandIntegratedManufacturingTechnology(NorthwesternPolytechnicalUniversity),MinistryofEducation,Xi’an710072)Abstract:Achattercontrolmethodforthemillingofaero-enginecasingsisstudiedinthispaper.The20calculationmethodofthestabilitylimitsaredeveloped.Andthedistributionofstabilitylobediagramisinvestigatedinonesinglecuttinglineaswellasindifferentcuttinglines.Thestabilitylobediagramwillpresentastaggeredcaseindifferentcuttinglines.Thenitisdifficulttooptimizethecuttingparametersfortheentiremillingprocess.Therefore,anoptimalselectionapproachofcuttingparametersbasedonsinglelinetoolpathisproposedtosuppresscuttingchatterinthewholematerialremovalprocess.25Keywords:chatter;thin-walledparts;aero-enginecasings;cuttingparametersoptimalselection0引言薄壁件具有重量轻、结构紧凑等特点，已经在航空工业中得到了广泛应用，如航空发动30机叶片、机匣、整体叶盘、整体叶轮等。这些零件都是飞机和发动机结构中不可缺少的组成部分，它们的制造技术是衡量一个国家制造能力的重要标志。然而，薄壁件在提升产品性能的同时也带来了新的难题和挑战。薄壁件的加工精度和表面质量要求高，同时几何结构复杂、材料难铣削、工艺刚性弱，从而导致加工过程中容易发生变形和振动。其中，由于铣削厚度变化效应引起的铣削颤振具35有不可忽略的破坏性。铣削颤振不仅会降低加工精度、破坏表面质量、限制加工效率，还会对机床和刀具的使用寿命以及工艺操作员的人身健康造成损害，严重时甚至会使加工过程无[1][2]法进行。目前，在测定工艺系统动力学参数的基础上，通过理论分析来优选铣削参数，使铣削过程的阻尼和刚度特性在短时间内快速变化，从而破坏颤振的产生和发展条件，可以[3][4]达到控制颤振的目的。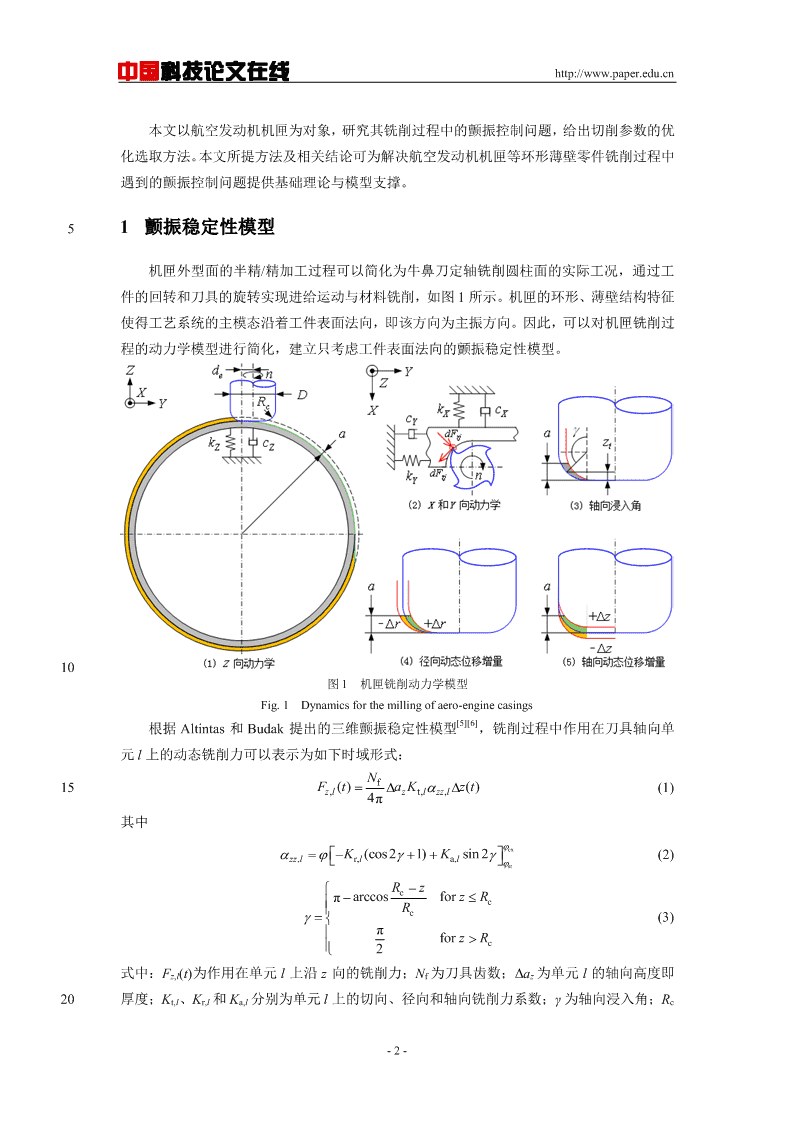40基金项目：教育部博士点基金(20136102110016)作者简介：周续（1987-），男，博士研究生，主要研究方向为多轴数控加工理论及智能加工技术通信联系人：张定华(1958-)，男，教授，博士研究生导师，主要研究方向为航空发动机制造技术.E-mail:dhzhang@nwpu.edu.cn-1- 中国科技论文在线http://www.paper.edu.cn本文以航空发动机机匣为对象，研究其铣削过程中的颤振控制问题，给出切削参数的优化选取方法。本文所提方法及相关结论可为解决航空发动机机匣等环形薄壁零件铣削过程中遇到的颤振控制问题提供基础理论与模型支撑。51颤振稳定性模型机匣外型面的半精/精加工过程可以简化为牛鼻刀定轴铣削圆柱面的实际工况，通过工件的回转和刀具的旋转实现进给运动与材料铣削，如图1所示。机匣的环形、薄壁结构特征使得工艺系统的主模态沿着工件表面法向，即该方向为主振方向。因此，可以对机匣铣削过程的动力学模型进行简化，建立只考虑工件表面法向的颤振稳定性模型。10图1机匣铣削动力学模型Fig.1Dynamicsforthemillingofaero-enginecasings[5][6]根据Altintas和Budak提出的三维颤振稳定性模型，铣削过程中作用在刀具轴向单元l上的动态铣削力可以表示为如下时域形式：Nf15Fzl,()taKzt,lzzl,zt()(1)4π其中ex(2)zzl,KKr,l(cos21)a,lsin2stRzcπarccosforzRcRc(3)πforzRc2式中：Fz,l(t)为作用在单元l上沿z向的铣削力；Nf为刀具齿数；Δaz为单元l的轴向高度即20厚度；Kt,l、Kr,l和Ka,l分别为单元l上的切向、径向和轴向铣削力系数；γ为轴向浸入角；Rc-2- 中国科技论文在线http://www.paper.edu.cn为刀具圆角半径；φst和φex分别为单元l上的切入角和切出角；Δz(t)为t时刻刀具的z向动态位移增量。根据刀具与工件之间交互作用的传递函数，刀具的z向动态位移增量可以表示为如下频域形式：iiTT5z(i)(1ecc)G(i)F(i)e(4)cczcz式中：Gz(iωc)为刀具与工件之间的传递函数，ωc为颤振频率；T为刀齿通过周期。因此，铣削过程中作用在刀具轴向单元l上的动态铣削力可以表示为如下频域形式：Fzl,c(i)NfiTaK(1ec)G(i)F(i)(5)zt,lzzl,zczc4πNfaKzt,lzzl,Re[Gz(ic)]Fz(ic)2π其中21dz10Re[Gzc(i)](6)k(1d22)(2d)2zzzzcdz(7)n式中：ωn为工艺系统的固有频率，kz和ξz分别为工件表面铣削位置处的刚度和阻尼比。将所有刀具轴向单元上的动态铣削力进行叠加，可以得到作用在整个刀具上的动态铣削力，如图2所示：Fz(ic)15Nm(8)faKRe[G(i)]F(i)zt,lzzl,zczc2πl1式中：m为刀具轴向单元数量。因此，可以得到刀具轴向单元厚度Δaz对应的稳定性极限切深及主轴转速：2πa(9)limmNfKt,lzzl,Re[Gz(ic)]l130cn(10)d21Nk(1)πarctanzf2zzd20式中：k为叶瓣序号。由于在颤振稳定性分析中有m个刀具轴向单元，所以对于整个刀具的稳定性极限切深为：ama(11)limlim-3- 中国科技论文在线http://www.paper.edu.cn图2刀具微元切片及其几何关系Fig.2Geometryandmechanicsofdiskl2稳定性叶瓣图分析5如图3所示，为某型航空发动机机匣模型，可以根据凸台的分布情况规划典型的材料切除方案，即沿周向铣削行进行材料切除。(1)机匣模型10(2)机匣加工划分的切削行情况图3机匣模型及其切削行划分Fig.3Aero-enginecasingmodelandcuttinglinesdivision如图4和图5所示，分别为机匣在切削行l1和不同切削行间加工时对应的稳定性叶瓣图。15图4切削行l1的稳定性叶瓣图Fig.4Stabilitylimitdiagramsincuttinglinel1-4- 中国科技论文在线http://www.paper.edu.cn图5不同切削行间的稳定性叶瓣图Fig.5Stabilitylimitdiagramsindifferentcuttinglines实际加工中的材料切除会使工艺系统的动力学特性发生显著变化，并造成稳定性叶瓣图5交错排列，铣削参数选取困难。为此，提出了一种面向分行刀位轨迹的铣削参数优选方法。该方法以单个刀位轨迹内的材料切除序列为第三维度，建立描述工艺系统动力学演化的三维稳定性叶瓣图。如图6和图7所示，为机匣加工铣削行l1和整个工序对应的三维稳定性叶瓣图。可以看出，在单个铣削行内，最初和最终铣削段对应的稳定性叶瓣图共同构成了整个铣削行的稳定性叶瓣图边界。由于单个铣削行内工艺系统的动力学特性变化幅度较小，因此三10维稳定性叶瓣图可以确定出较大的稳定参数区域，提供较宽的主轴转速区域和较大的稳定极限切深选择。而在整个工序内，三维稳定性叶瓣图确定的稳定参数区域较小，可优化选择的主轴转速区域较窄，可优化选择的稳定极限切深较小，造成整个加工过程中动态响应的容错能力降低，加工效率下降。15图6切削行l1的三维稳定性叶瓣图Fig.63Dstabilitylimitdiagramsincuttinglinel1图7不同切削行间的三维稳定性叶瓣图Fig.73Dstabilitylimitdiagramsindifferentcuttinglines-5- 中国科技论文在线http://www.paper.edu.cn3主轴转速分行优选如图8所示，为机匣加工铣削行l1对应的铣削参数优选结果。机床许用的最大主轴转速为8000rpm，半精加工工序选用的铣削深度为0.5mm。则从铣削行l1对应的动态响应控制图上可以看出，能够保证不发生铣削颤振的主轴转速范围为3175rpm~3779rpm，并且当主轴转5速选取在3702rpm附近时会发生强迫振动。选取主轴转速的调整区间为200rpm，则选取主轴转速可选范围的中间值3477rpm为铣削行l1使用的主轴转速。主轴转速3377rpm~3577rpm区间对应的容错切深为0.638mm，即该区间内允许的轴向切深波动范围为0.138mm。当强迫振动区位于主轴转速许用区间中部造成主轴转速难以选取时，优先在许用区间右侧进行主轴转速选取，此时可以获取较大的容错切深，同时为了保证稳定铣削可以适当缩小主轴转速10的调整区间。图8铣削行l1对应的主轴转速优选结果Fig.8Spindlespeedchoiceresultsincuttinglinel1如图9所示，为机匣加工铣削行l5对应的主轴转速分布情况。由于在铣削行l5中存在凸15台结构，为了避免发生碰撞干涉，在规划刀位轨迹时需要在凸台之间进行反复的进刀/退刀操作。因此，可以实现在每一个铣削段处优选一个主轴转速，在进刀/退刀过程中进行主轴转速变化，从而有效避免加工过程中进行主轴转速变化而产生的铣削凹槽。同时，由于在机匣加工的每一个铣削行内，工艺系统的动力学特性变化幅值都较小，因此可以针对单个铣削行优选一个主轴转速。如图10所示，为机匣加工各铣削行对应的主轴转速分布情况。可以20看出，每一个铣削行对应一个优选的主轴转速，保证该铣削行的稳定铣削。图9切削行l5的主轴转速优选结果Fig.9Spindlespeedchoiceresultsincuttinglinel525图10不同切削行的主轴转速优选结果Fig.10Spindlespeedchoiceresultsindifferentcuttinglines-6- 中国科技论文在线http://www.paper.edu.cn4结论本文建立了机匣铣削过程的颤振稳定性模型，计算并分析了机匣沿周向切削行进行铣削的稳定性叶瓣图，针对不同切削行间稳定性叶瓣图交错排列、切削参数难以优化选取的问题，提出了面向分行刀位轨迹的主轴转速优选方法，采用优化选取的切削参数进行加工可以有效5避免了机匣整个铣削过程中的颤振。[参考文献](References)[1]TobiasSA.Machine-toolvibration[M].BlackieandSonsLimited,Glasgow,1965.[2]TlustyJ,PolacekM.Thestabilityofmachinetoolsagainstself-excitedvibrationsinmachining[C].ProceedingsoftheInternationalResearchinProductionEngineering,1963,10September9-12,Pittsburgh,465-474.[3]SeguyS,InspergerT,ArnaudL,etal.Suppressionofperioddoublingchatterinhigh-speedmillingbyspindlespeedvariation[J].MachiningScienceandTechnology,2011,15(2):153-171.[4]CampaFJ,LopezdeLacalleLN,.UrbicainG,etal.Criticalthicknessanddynamicstiffnessforchatteravoidanceinthinfloorsmilling[J].AdvancedMaterialsResearch,2011,188:116-121.15[5]ALTINTASY.Analyticalpredictionofthreedimensionalchatterstabilityinmilling[J].JSMEInternationalJournal.SeriesC,MechanicalSystems,MachineElementsandManufacturing,2001,44(3):717-723.[6]OZTURKE,BUDAKE.Dynamicsandstabilityoffive-axisball-endmilling[J].TransactionsoftheASMEJour-nalofManufacturingScienceandEngineering,2010,132(2):021003-1-13.20-7-'