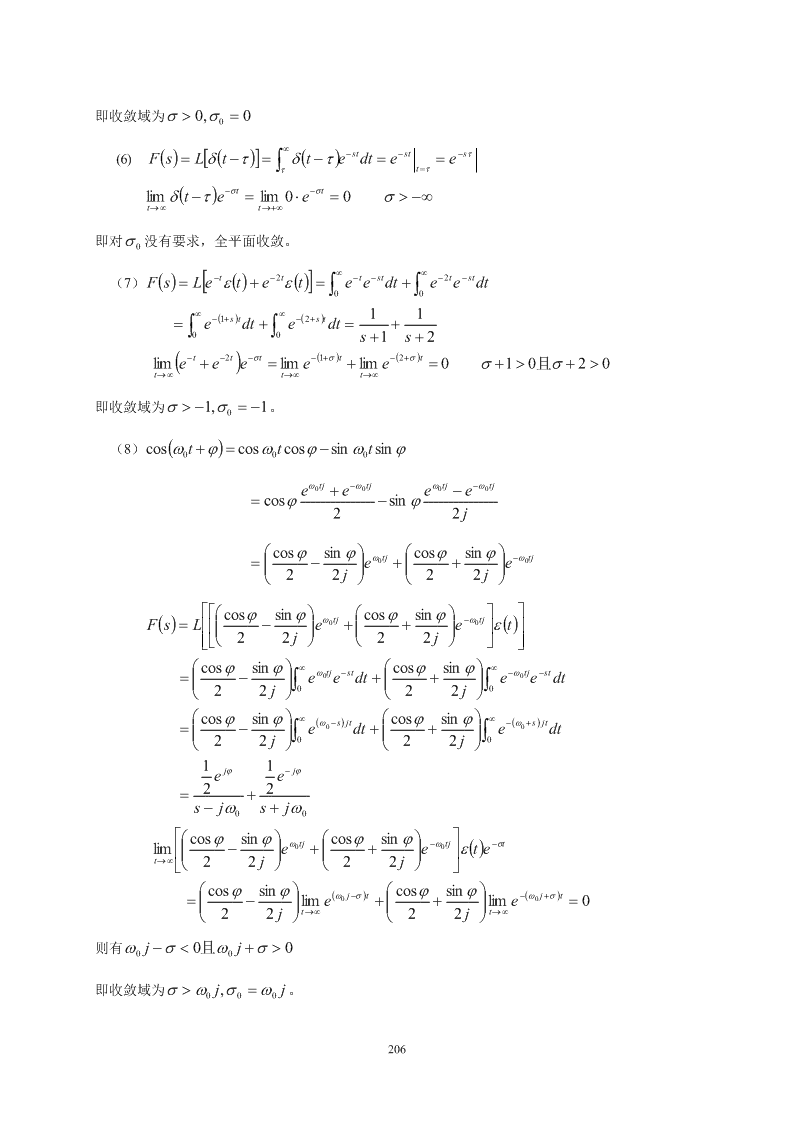信号与系统 第四章答案.pdf 45页

'http://www.benxiao.com第四章连续时间信号与系统的复频域分析4.1学习重点1、拉普拉斯变换的定义式，收敛域，能根据拉普拉斯变换的定义式求一些常用信号的拉普拉斯变换。2、熟练掌握拉普拉斯变换的基本性质（特别是时移性、频移性、时域微分、频域微分、初值定理、终值定理、卷积定理等性质）及其应用。3、能应用部分分式法展开法、留数法，求解拉普拉斯反变换。4、利用拉普拉斯进行连续时间信号的复频域分析，分析电路、s域元件模型，能求解线性时不变系统的响应，包括全响应、零输入响应、零状态响应，以及冲激响应和阶跃响应。5、深刻理解复频域系统函数H(s)的定义、物理意义及其与系统特性的关系，并能熟练应用于连续时间信号的复频域分析。6、系统的复频域方框图表示与模拟。7、了解系统函数的零、极点与系统特性的关系，会画零、极点图，会根据零、极点图求系统函数H(s)。8、系统稳定性及其判断方法。9、用MATLAB进行连续时间信号与系统的复频域分析4.2教材习题同步解析4.1求下列信号的拉普拉斯变换及其收敛域，并画出零极点图和收敛域。-atat（1）ee(t),a<0（2）-ee(-t),a>0204 at-at（3）ee(t),a>0（4）e,a>0（5）e(t-4)（6）d(t-t)-t-2t（7）ee(t)+ee(t)（8）cos(wt+j)e(t)0【知识点窍】主要考察拉普拉斯变换定义及收敛域求法。¥-st【逻辑推理】单边拉普拉斯变换定义：F(s)=f(t)edt。若满足s>s，使得ò0-0lim()-st=0-stfte，则f(t)e在s>s的全部范围内收敛。0t®¥解：¥¥()1-at-at-st-a+st（1）F(s)=L[ee(t)]=òeedt=òedt=00s+a-at-st-(a+s)tlimee=lime=0s+a>0t®¥t®¥即收敛域为s>-a,s=-a。000()1at-at-st-a+st（2）F(s)=L[-ee(-t)]=ò-¥eedt=ò-¥edt=-s+aat-st(a-s)tlim-ee=lime=0a-s<0t®¥t®¥即收敛域为s>a,s=a。0¥¥()1atat-sta-st（3）F(s)=L[ee(t)]=òeedt=òedt=00s-aat-st(a-s)tlimee=lime=0a-s<0t®¥t®¥即收敛域为s>a,s=a。00¥-atat-st-at-st（4）F(s)=L[ee(t)]=òeedt+òeedt-¥00(a-s)t¥-(a+s)t11=òedt+òedt=+-¥0s-as+a-at-st-(a+s)tlimee=lime=0a+s<0即s>-at®+¥t®+¥at-st(a-s)tlimee=lime=0a-s>0即s0t®¥t®+¥205 即收敛域为s>0,s=00¥-st-st-st(6)F(s)=L[d(t-t)]=òd(t-t)edt=e=ett=t()-st-stlimdt-te=lim0×e=0s>-¥t®¥t®+¥即对s没有要求，全平面收敛。0¥¥-t-2t-t-st-2t-st（7）F(s)=L[ee(t)+ee(t)]=òeedt+òeedt00¥-(1+s)t¥-(2+s)t11=òedt+òedt=+00s+1s+2(-t-2t)-st-(1+s)t-(2+s)tlime+ee=lime+lime=0s+1>0且s+2>0t®¥t®¥t®¥即收敛域为s>-1,s=-1。0（8）cos(wt+j)=coswtcosj-sinwtsinj000ew0tj+e-w0tjew0tj-e-w0tj=cosj-sinj22j=æçcosj-sinjö÷ew0tj+æçcosj+sinjö÷e-w0tjç÷ç÷è22jøè22jø()ééæcosjsinjöw0tjæcosjsinjö-w0tjù()ùFs=Lêêçç-÷÷e+çç+÷÷eúetúêëëè22jøè22jøûúûæcosjsinjö¥wtj-stæcosjsinjö¥-wtj-st=ç-÷e0edt+ç+÷e0edtçè22j÷øò0çè22j÷øò0æcosjsinjö¥(w-s)jtæcosjsinjö¥-(w+s)jt=ç-÷e0dt+ç+÷e0dtçè22j÷øò0çè22j÷øò01jj1-jjee22=+s-jws+jw00liméæçcosj-sinjö÷ew0tj+æçcosj+sinjö÷e-w0tjùe(t)e-stêç÷ç÷út®¥ëè22jøè22jøû=æçcosj-sinjö÷lime(w0j-s)t+æçcosj+sinjö÷lime-(w0j+s)t=0çè22j÷øt®¥çè22j÷øt®¥则有wj-s<0且wj+s>000即收敛域为s>wj,s=wj。000206 4.2求图4.1所示信号的拉普拉斯变换。【知识点窍】主要考察拉普拉斯变换基本性质【逻辑推理】首先分析图形，看是由哪些基本信号的图形组合，然后通过基本信号的拉普拉斯变换和拉普拉斯变换基本性质来求取其拉普拉斯变换。图4.1解：（a）x(t)=e(t)-e(t-T)1因e(t)«，根据拉普拉斯变换时延特性，有s()11-sT1(-sT)Xs=-e=1-esss（b）x(t)=e(t)+e(t-1)-e(t-2)-e(t-3)1因e(t)«，根据拉普拉斯变换时延特性，有s()11-s1-2s1-3s1(-s-2s-3s)Xs=+e-e-e=1+e-e-esssss111（c）x(t)=t[e(t)-e(t-T)]=te(t)-(t-T)e(t-T)-e(t-T)TTT11因e(t)«，te(t)«，根据拉普拉斯变换时延特性，有2ss()11-sT1-sTXs=-e-e22TssTsæ1ö11（d）x(t)=ç-t+1÷[e(t)-e(t-T)]=-(t-T)e(t)+(t-T)e(t-T)èTøTT11因e(t)«，te(t)«，根据拉普拉斯变换时延特性，有2ss()111-sTXs=-++e22TssTs207 2æ4öæTöæ2ö（e）x(t)=te(t)+ç-t+2÷eçt-÷+çt-2÷e(t-T)TèTøè2øèTø2()4æTöæTö2()()=tet-çt-÷eçt-÷+t-Tet-TTTè2øè2øT11因e(t)«，te(t)«，根据拉普拉斯变换时延特性，有2sssT24-2-sTX(s)=-e2+e222TsTsTssT-2-4e2+2e-sT=2Ts（f）x(t)=sinpt[e(t)-e(t-p)]psinpte(t)«22s+pjpt-jptée-eùL[sinpte(t-p)]=Lêe(t-p)úë2jû-(s-jp)p-(s+jp)p1é¥jpt-st¥-jpt-stù1éeeù=êëòpeedt-òpeedtúû=ê-ú2j2jës-jps+jpû所以é-(s-jp)p-(s+jp)pùp1eeX(s)=22-ê-ús+p2jës-jps+jpû()-spjp2()-sp-jp2p1s+jpee-s-jpee=-×2222s+p2js+p2222(jp-jp)(jp-jp)p1-spse-e+jpe+e=-e×2222s+p2js+p22p-spssinpt+pcospt=-e2222s+ps+p-sp(22)p-essinpt+pcospt=22s+p4.3图4.2所示的每一个零极点图，确定满足下述情况的收敛域。2t（1）f(t)的傅里叶变换存在（2）f(t)e的傅里叶变换存在（3）f(t)=0,t>0（4）f(t)=0,t<5【知识点窍】主要考察拉普拉斯变换的零极点分布特性。【逻辑推理】首先由零极点写出拉普拉斯变换式，再利用反变换求取其原信号，即可求取其收208 域。图4.2解：由图4.2（a）得()k1k1é11ùk1t-tFs==-即得f(t)=[e-e]e(t)(s-1)(s+1)2êës-1s+1úû2由图4.2（b）图得()k2k2é11ùk23t-3tFs==-即得f(t)=[e-e]e(t)(s-3)(s+3)6êës-3s+3úû2由图4.2（c）图得()k3k3é11ùk3-t-3tFs==-即得f(t)=[e-e]e(t)(s+3)(s+1)2êës+1s+3úû2（1）f(t)的傅里叶变换存在，对于由图4.2（a）来说，其收敛域为()-stk1[t-t]-stK1[(1-s)t-(1+a)t]limfte=lime-ee=lime-e=0t®¥t®¥2t®¥2则由此可得1-a<0È1+a>0即收敛域为a>1同理，对于图4.2（b）来说，其收敛域为：s>3对于图4.2（c）来说，其收敛域为：a>-12t（2）f(t)e的傅里叶变换存在，对于由图4.2（a）来说，其收敛域为()2t-stk1[3tt]-stK1[(3-s)t(1-a)t]limftee=lime-ee=lime-e=0t®¥t®¥2t®¥2由此可得其收敛域为：s>3同理，对于对于图4.2（b）来说，其收敛域为：s>5209 对于图4.2（c）来说，其收敛域为：a>1（3）（4）情况下，收敛域均为：-¥-1或-30该信号的极点位于s平面的虚轴上，所以该信号为等幅振荡信号。（c）由如图4.3（c）所示的零极点图，可得到拉氏变换式为(s+j)(s-j)F(s)=(s-1)(s+1)(s+2)拉氏变换的收敛域内不应包含象函数的任何极点，所以信号可能的收敛域为s<-2或s>1或-20【知识点窍】主要考察拉普拉斯变换定义与收敛域算法。【逻辑推理】首先由收敛的条件判断拉氏变换是否存在，然后再利用拉氏变换定义式求取其拉氏变换。-stt1解：（1）limte(t)e=lim=lim=0s>0ststt®¥t®¥et®¥se即s=0，收敛坐标位于坐标原点，收敛轴即虚轴，收敛域为S平面的右半平面。0¥1()[()]-stFs=Ltet=tedt=ò0s222-stt2（2）limte(t)e=lim=lim=0s>0st2stt®¥t®¥et®¥se即s=0，收敛坐标位于坐标原点，收敛轴即虚轴，收敛域为S平面的右半平面。0¥2()[2()]2-stFs=Ltet=tedt=ò0s3-2t-stt1（3）limtee(t)e=lim=lim=0s+2>0(s+2)t(s+2)tt®¥t®¥et®¥(s+2)e即s>-2，s=-20¥1()[-2t()]-2t-stFs=Lteet=teedt=ò0(s+2)222t-stt-st（4）limee(t)e=lime=0t®¥t®¥满足上式的s值不存在，所以该信号的拉普拉斯变换不存在。tte-ste-st（5）limee(t)e=lime=0t®¥t®¥满足上式的s值不存在，所以该信号的拉普拉斯变换不存在。211 -st-t-stt-st（6）limf(t)e=limee(t)e+limee(t)et®¥t®-¥t®+¥-(s+1)t(1-s)t=lime+lime=0s+1<0且1-s<0t®-¥t®+¥满足上式的s值不存在，所以该信号的拉普拉斯变换不存在。4.6利用拉普拉斯变换的性质，求下列信号的拉氏变换，并画出零极点图。-t-t（1）(t+1)e(t-1)（2）tee(t-t)（3）(t+1)ee(t)2-at（4）tee(t)（5）sinpt[e(t)-e(t-1)]（6）sinwtcoswte(t)2（7）sinwte(t-t)（8）sinw(t-t)e(t)（9）sinte(t)-atsinat（10）sinte(t)（11）tecoswte(t)（12）e(t)ttttd-at（13）ò0sinptdt（14）ò0ò0sinpxdxdt（15）[esinwte(t)]dt22-a(t-t0)ddsinpt（16）esin(wt+q)e(t)（17）[sinpte(t)]（18）e(t)22dtdtt-atætö（19）òtsintdt（20）efç÷e(t)0èbø【知识点窍】主要考察拉普拉斯变换性质以及零极点图画法。【逻辑推理】首先分析每一个信号，看是由哪些基本信号的图形组合，然后通过基本信号的拉普拉斯变换和拉普拉斯变换基本性质来求取其拉普拉斯变换。解：（1）(t+1)e(t-1)=(t-1)e(t-1)+2e(t-1)11因为tee(tt)««()2ss12--ss1--ssæö121s+由时移特性可得：F(see)=+=eeç÷2+=22sssèøss其零极点图如图4.4（a）所示。（2）设f(t)=te(tt-=t)(-t)e(tt-t)+-tet()011因为tee(tt)««()2ss1--sstttt1--ssttæö11s+由时移特性可得：F(see)=+=eeç÷t+=022sssèøss212 --ttt(s++11)-+(s1)t由频移特性可得：teet(t-)=f(t)e«F(se+=1)002(s+1)其零极点图如图4.4（b）所示。（3）设f(t)=(t+1)e(t)=+tee(tt)()011因为tee(tt)««()2ss111s+由时移特性可得：Fs()=+=022sss--tts+2由频移特性可得：(tet+=11)e()f(t)e«Fs(+=)002(s+1)其零极点图如图4.4（c）所示。nn!222!（4）因为tte()«即得tte()«=n+133sss2-at2由频移特性可得：tete()«3(sa+)其零极点图如图4.4（d）所示。（5）因为sinptéùëûe(t)--e(t11)=sinpte(t)--sinpett()=sinptte()+sinpe(tt--11)()p又因为sinpett()«22s+pp-s由拉氏变换时移性质有sinpe(t-11)(te-«)22s+pp-s由线性性质即得sinptéùee(t)--(te11)«+()ëû22s+p其零极点图如图4.4（e）所示。1（6）因为sinwtcoswte(t)=sintt(2we)()22w又因为sintt2we()«22s+(2w)w由线性性质即得sinwtcoswett()«22s+(2w)其零极点图如图4.4（f）所示。（7）因为213 1jwwt-jtsintwe(t-t)=(e--et)et()2jjjwt-wteejw(t-t)--jtwt()=ee(t-t)--etet()22jj±at1又因为ete()«samjwwt11-jt即可得eee(t)««et()s-+jwwsj由拉氏变换的时移特性得jw(t-t)11--sstt--jtwt()ee(t-t)«eeet(te-«)s-+jwwsj由拉氏变换线性特性可得jjwt-wtee11--ssttsintwet(t-)«-ee22js-+jwwjsjjjwt-wt1éùee-st=-êúe2jëûs-+jwwsjjwt--jwtjjwtwt1s(e-e)++jw(ee)-st=e222js+w1s22jsinwt+jwcoswt-st=e222js+wssinwt+wcoswt-st=e22s+w其零极点图如图4.4（g）所示。（8）因为1jw(t-t)--jtwt()sinw(tte-t)ee()=-(et)()2j-jjwtwteejwwt-jt=-eee(t)et()22jj±at1又因为ete()«samjwwt11-jt即可得eee(t)««et()s-+jwwsj由拉氏变换线性特性可得214 -jjwtwtee11sinw(tt-te)()«-22js-+jwwjsj-jjwtwt1éùee=-êú2jsëû-+jwwsj--jwtjwtjjwtwt1s(ee-)++jw(ee)=222js+w1-+s22jsinwtjwcoswt=222js+w-+ssinwtwcoswt=22s+w其零极点图如图4.4（h）所示。21-cost211（9）因为sinte(t)=e(t)=-ee(t)cos2tt()2221s又因为e(t)««costtwe()22ss+w由拉氏变换线性特性可得2211swsintte()«-=222222ss+w2(s+w)其零极点图如图4.4（i）所示。（10）设f(t)=sinte(t)+sin(tt--p)ep()01-sp则由题4.6（5）可知f(te)«+(1)02s+1¥则sinte(t)=--åft(np)ep(tn)0n=0-sp111+e由拉氏变换时移特性可知sinte(t)«=Fs()--sspp021-e11-+es其零极点图如图4.4（j）所示。22s-w（11）因为tcoswte(t)«(22)2s+w由拉氏变换的频移特性可得()22-at()s+a-wtecoswtet«2[()22]s+a+w其零极点图如图4.4（k）所示。215 w（12）因为sinwte(t)«22s+wa即得sinate(t)«22s+a由S域积分定理可得sinat¥a¥1æs1ös1¥pæsöæsöte(t)«òss2+a2ds1=òs2dça÷=arctanas=2-arctançèa÷ø=arctançèa÷ø1æs1öèøç÷+1èaø其零极点图如图4.4（l）所示。w（13）因为sinwte(t)«22s+wp即得sinpte(t)«22s+p由时域积分定理可得t1ppsinptdt«=ò022(22)ss+pss+p其零极点图如图4.4（m）所示。w（14）因为sinwte(t)«22s+wp即得sinpte(t)«22s+p由时域积分定理可得tt1ppsinpxdxdt«=ò0ò02222(22)ss+pss+p其零极点图如图4.4（n）所示。w（15）因为sinwte(t)«22s+w由拉氏变换的频移特性可得-at()wesinwtet«()22s+a+w由拉氏变换时域微分定理可得d[-at()]wesinwtet«s22dt(s+a)+w其零极点图如图4.4（0）所示。216 （16）因为sin(wt+q)e(t)=[sin(wt)cosq+cos(wt)sinq]e(t)-a(t-t0)at0-atat0-at所以esin(wt+q)e(t)=ecosq[esin(wt)e(t)]+esinq[ecos(wt)e(t)]ws又因为sinwte(t)«coswte(t)«2222s+ws+w由拉氏变换的频移特性可得-at()w-at()sesinwtet«ecoswtet«()22()22s+a+ws+a+w由拉氏变换的线性特性有：e-a(t-t0)sin(wt+q)e(t)«eat0wcosq+ssinq()22s+a+w其零极点图如图4.4（p）所示。p（17）因为sinpte(t)«22s+p22dps由拉氏变换的时域微分定理得[sinpte(t)]«2(22)dts+p其零极点图如图4.4（q）所示。2dsinptdcospt2（18）因为e(t)=pe(t)=-psinpte(t)2dtdtp又因为sinpte(t)«22s+p23dsinptp由拉氏变换线性特性得e(t)«-222dts+p其零极点图如图4.4（r）所示。ttttt（19）因为tsintdt=-tdcost=-tcost+costdt=-tcoste(t)+costdtò0ò00ò0ò02s-1s由于tcoste(t)«coste(t)«222(s+1)s+1由拉氏变换的时域积分特性和线性特性可得2ts-11s2tsintdt«-+=ò0(s2)2s2+1(2)2+1ss+1其零极点图如图4.4（s）所示。217 （20）设f(t)e(t)«F(s)ætö由拉氏变换的尺度变换特性可得fç÷e(t)«bF(bs)èbø-atætö由拉氏变换的频移特性可得efç÷e(t)«bF[b(s+a)]èbøjwjwjw（二阶）（二阶）╳（二阶）╳sss╳11-1-1--2-1-t2（a）（b）（c）jwjwjw╳（三阶）╳jpj2wsss╳-a╳╳-jp-j2w（d）（e）（f）jwjwjw╳jw╳jw╳jwsss-wctg(wt)╳-jw╳-wctg(wt)╳-jw-jw（g）（h）（i）jwjw╳j╳jws╳-as-a-w-a+w╳-j╳-jw（j）（k）218 jwjwjw╳jp╳jps（二阶）╳╳ss╳-jp╳-jp（l）（m）（n）jwjw╳jw╳jws-as-a-wctgq-jw╳╳-jw（o）（p）jwjwjw╳jp╳jp╳j(二阶)(二阶)s-as-as╳-j(二阶)╳-jp╳-jp（q）（r）（s）图4.44.7求图4.5所示单边周期信号的拉氏变换。图4.5219 【知识点窍】主要考察拉普拉斯变换时移特性。【逻辑推理】首先确定信号第一周期的信号，然后利用时移特性进行求解。即周期信号的拉普1拉斯变换等于其第一周期波形的拉普拉斯变换式乘以。-sT1-e解：（a）该信号第一周期内波形可表示为()()æTöf0t=et-eçt-÷è2ø其拉普拉斯变换式为STST--1e21-e2F(s)=-=0sss由拉氏变换的时移特性可得ST-11-e2F(s)=F(s)=-ST0(-ST)1-es1-e（b）该信号第一周期内波形可表示为11f(t)=te(t)-(t-2)e(t-2)+(t-4)e(t-4)022其拉普拉斯变换式为-2S-4S-2S-4S1ee1-2e+eF(s)=-+=022222ss2s2s由拉氏变换的时移特性可得11F(s)=F(s)=F(s)-ST0-4S01-e1-e-2S-4S1-2e+e=2(-4S)2s1-e4.8求下列象函数的拉氏反变换f(t)。2-ss+3ses（1）F(s)=（2）F(s)=（3）F(s)=22s+2s+2s+2s+5(s+1)(s+2)22ss-1s-s+1（4）F(s)=（5）F(s)=ln（6）F(s)=3232s+3s+7s+5ss-s【知识点窍】主要考察拉普拉斯反变换求法。【逻辑推理】将以上式子先用部分分式展开，变成常用信号的拉氏变换，然后再进行拉氏反变220 换或者利用拉氏变换的基本性质来求反变换。s+3s+3s+12解：（1）F(s)===+2222s+2s+2(s+1)+1(s+1)+1(s+1)+1对上式进行拉普拉斯反变换，即得：()-t()-t()-t[]()ft=ecostet+2esintet=ecost+2sintet2-sseé2s+5ù-sé2s+5ù-s（2）F(s)=2=ê1-2úe=ê1-2úes+2s+5ës+2s+5ûë(s+1)+4ûé2(s+1)32ù-s=ê1-2-×2úeë(s+1)+42(s+1)+4û-s2(s+1)-s32-s=e-e-×e22(s+1)+42(s+1)+4对上式进行拉普拉斯反变换，即得：()()-(t-1)()()3-(t-1)()()ft=dt-1-2ecos2t-1et-1-esin2t-1et-12sKK12（3）F(s)==+(s+1)(s+2)s+1s+2其中K=(s+1)F(s)=-11s=-1K=(s+2)F(s)=22s=-2所以12F(s)=-+s+1s+2对上式进行拉普拉斯反变换，即得：()(-t-2t)()ft=-e+2eet22ss（4）F(s)==32()(2)s+3s+7s+5s+1s+2s+5KKK123=++s+1s+1-2js+1+2j其中1K=(s+1)F(s)=1s=-14221 3+4jK=(s+1-2j)F(s)=2s=-1+2j83-4jK=(s+1+2j)F(s)=3s=-1-2j8所以113+4j13-4j1F(s)=×+×+×4s+18s+1-2j8s+1+2j对上式进行拉普拉斯反变换，即得：()é1-t3+4j(-1+2j)t3-4j-(1+2j)tù()ft=e+e+eetêúë488ûé1-t3-t(2jt-2jt)1-t(2jt-2jt)ù()=e+ee+e+jee-eetêúë482ûé1-t3-t-tù()=e+ecos2t-esin2tetêúë44û1-t[]()=e1+3cos2t-4sin2tet4s-1（5）F(s)=lnsdF(s)sæ1ö111则有=×ç-÷=-=-2()dss-1èsøss-1ss-1对上式进行拉普拉斯反变换，即得：-1édF(s)ù-1é11ù()t()L=L-=et-eetêúêúëdsûëss-1û根据拉普拉斯变换的微分特性，有：()()t()-tft=et-eet则有()t()()et-eet1(t)()ft==e-1et-tt22s-s+1s-s+111（6）F(s)===-322()2s-sss-1s-1s对上式进行拉普拉斯反变换，即得：()(t)()ft=e-tet4.9求下列各象函数的原函数f(t)的初值与终值。222 2s+3s+5s（1）F(s)=（2）F(s)=（3）F(s)=2242s+3s+2s(s+2s+4)s+5s+4-ses+311（4）F(s)=（5）F(s)=（6）F(s)=+2325s(s-2)(s+1)(s+2)ss+1【知识点窍】主要考察初值定理、终值定理。【逻辑推理】若有f(t)«F(s)s>s且f(t)连续可导和limsF(s)存在，则0s®¥(+)()()f0=limft=limsFst®0+s®¥若有f(t)«F(s)s>s，且limf(t)存在，则0t®¥f(¥)=limf(t)=limsF(s)t®¥s®0解：初值定理的应用条件是，F(s)必须是真分式；终值定理应用的条件是：（1）F(s)的极点必须在s平面的左半开平面。（2）在s=0处，F(s)只能有一阶极点。也就是说，终值定理只有在f(t)有终值的情况下才能应用。例如，当f(t)为周期函数时，终值定理就不适用了。s+3s+3（1）F(s)==2()()s+3s+2s+1s+2(+)()()s+3é2ùf0=limft=limsFs=lims×=lim1-=1t®0+s®¥s®¥(s+1)(s+2)s®¥êës2+3s+2úû()()()é2ùf¥=limft=limsFs=lim1-=0t®¥s®0s®0êës2+3s+2úû22s+5s+5（2）F(s)==(2)()()ss+2s+4ss+1+3js+1-3j22(+)()()s+5s+5f0=limft=limsFs=lims×=limt®0+s®¥s®¥s(s2+2s+4)s®¥s2+2s+451+2s=lim=1s®¥241++2ss2s+55f(¥)=limf(t)=limsF(s)=lim=t®¥s®0s®0s2+2s+44223 ss（3）F(s)==42(2)(2)s+5s+4s+1s+4因F(s)在jw轴上有两对共轭极点，故与F(s)对应的f(t)不存在终值。2(+)()()ssf0=limft=limsFs=lims×=limt®0+s®¥s®¥s4+5s2+4s®¥s4+5s2+41=lim=0s®¥24s+5+2s-se（4）F(s)=2()35ss-2因F(s)在s平面的右半开平面上有极点s=2，且在s=0处，F(s)有二阶极点，故与F(s)对应的f(t)不存在终值。-s-s(+)()()eef0=limft=limsFs=lims×=lim=0t®0+s®¥s®¥5s2(s-2)3s®¥5s(s-2)3s+3（5）F(s)=()2()s+1s+2+s+3f(0)=limf(t)=limsF(s)=lims×=0t®0+s®¥s®¥(s+1)2(s+2)s+3f(¥)=limf(t)=limsF(s)=lims×=0t®¥s®0s®0(s+1)2(s+2)11（6）F(s)=+ss+1+æ11öæsöf(0)=limf(t)=limsF(s)=lims×ç+÷=limç1+÷=2t®0+s®¥s®¥èss+1øs®¥ès+1øæsöf(¥)=limf(t)=limsF(s)=limç1+÷=1t®¥s®0s®0ès+1ø4.10已知LTI因果系统的系统函数H(s)及输入信号f(t)，求系统的响应y(t)。2s+3s+4-t（1）H(s)=,f(t)=e(t)（2）H(s)=,f(t)=ee(t)22s+6s+8s(s+3s+2)224 2s+2s-2ts+1-t（3）H(s)=,f(t)=ee(t)（4）H(s)=,f(t)=tee(t)22s(s+9)s+5s+6【知识点窍】主要考察利用拉氏变换求解系统的响应。【逻辑推理】首先求取激励的拉氏变换，然后根据系统函数的特性求出系统响应的拉氏变换，再求其拉氏反变换即得系统的响应。1解：（1）当f(t)=e(t)时，有F(s)=s则有2s+312s+3Y(s)=H(s)×F(s)=×=2()()s+6s+8sss+2s+4KKK123=++ss+2s+4其中3K=sY(s)=1s=081K=(s+2)Y(s)=2s=-245K=(s+4)Y(s)=-3s=-48所以311151Y(s)=×+×-×8s4s+28s+4对上式进行拉普拉斯反变换，即得系统响应为()3()1-2t()5-4t()1(-2t-4t)()yt=et+eet-eet=3+2e-5eet8488-t1（2）当f(t)=ee(t)时，有F(s)=s+1则有s+41s+4Y(s)=H(s)×F(s)=×=(2)()2()ss+3s+2s+1ss+1s+2K11K12K2K3=+++2(s+1)s+1ss+2其中()2()K=s+1Ys=-311s=-1225 d2K=[(s+1)Y(s)]=-112dss=-1K=sY(s)=22s=0K=(s+2)Y(s)=-13s=-2所以-3-12-1Y(s)=+++2(s+1)s+1ss+2对上式进行拉普拉斯反变换，即得系统响应为()-t()-t()-2t()(-t-t-2t)()yt=-3teet-eet+2-eet=-3te-e+2-eet-2t1（3）当f(t)=ee(t)时，有F(s)=s+2则有2s+2s1113Y(s)=H(s)×F(s)=H(s)=×==×(2)22ss+9s+2s+93s+9对上式进行拉普拉斯反变换，即得系统响应为1y(t)=sin3te(t)3-t1（4）当f(t)=tee(t)时，有F(s)=()2s+1则有s+111Y(s)=H(s)×F(s)=H(s)=×=22s+5s+6(s+1)(s+1)(s+2)(s+3)KKK123=++s+1s+2s+3其中1K=(s+1)Y(s)=1s=-12K=(s+2)Y(s)=-12s=-21K=(s+3)Y(s)=3s=-32所以226 11111Y(s)=×-+×2s+1s+22s+3对上式进行拉普拉斯反变换，即得系统响应为()æ1-t-2t1-3tö()yt=çe-e+e÷etè22ø4.11计算下列微分方程描述的因果系统的系统函数H(s)。若系统最初是松弛的，而且f(t)=e(t)，求系统的响应y(t)。（1）y""(t)+4y"(t)+3y(t)=f"(t)+f(t)（2）y""(t)+4y"(t)+5y(t)=f"(t)-t如果f(t)=ee(t)，系统的响应y(t)又是什么？【知识点窍】主要考察利用拉氏变换求解系统的响应。【逻辑推理】首先由系统的微分方程求取系统函数，然后求出系统响应的拉氏变换，再求其拉氏反变换即得系统的响应。1解：Ⅰ.当f(t)=e(t)时，有F(s)=s（1）由微分方程y""(t)+4y"(t)+3y(t)=f"(t)+f(t)，可得系统函数s+1s+11H(s)===2()()s+4s+3s+1s+3s+3则有()()()11K1K2Ys=Hs×Fs=×=+s+3sss+31其中：K=sY(s)=1s=031K=(s+3)Y(s)=-2s=-33所以1111Y(s)=×-×3s3s+3对上式进行拉普拉斯反变换，即得系统响应为()1()1-3t()1(-3t)()yt=et-eet=1-eet333227 （2）由微分方程y""(t)+4y"(t)+5y(t)=f"(t)，可得系统函数sH(s)=2s+4s+5则有s111Y(s)=H(s)×F(s)=×==222s+4s+5ss+4s+5(s+2)+1对上式进行拉普拉斯反变换，即得系统响应为()-2t()yt=esintet-t1Ⅱ.当f(t)=ee(t)时，有F(s)=s+1（1）由微分方程y""(t)+4y"(t)+3y(t)=f"(t)+f(t)，可得系统函数s+1s+11H(s)===2()()s+4s+3s+1s+3s+3则有()()()11K1K2Ys=Hs×Fs=×=+s+3s+1s+1s+31其中：K=(s+1)Y(s)=1s=-121K=(s+3)Y(s)=-2s=-32所以1111Y(s)=×-×2s+12s+3对上式进行拉普拉斯反变换，即得系统响应为()1-t()1-3t()1(-t-3t)()yt=eet-eet=e-eet222（2）由微分方程y""(t)+4y"(t)+5y(t)=f"(t)，可得系统函数sH(s)=2s+4s+5则有s1sY(s)=H(s)×F(s)=×=2()(2)s+4s+5s+1s+1s+4s+5K1K2K3=++s+2-js+2+js+1228 1-3j其中：K=(s+2-j)Y(s)=1s=-2+j41+3jK=(s+2+j)Y(s)=2s=-2-j41K=(s+1)Y(s)=-3s=-12所以1-3j11+3j111Y(s)=+-4s+2-j4s+2+j2s+1对上式进行拉普拉斯反变换，即得系统响应为()é1-3j(-2+j)t1+3j(-2-j)t1-tù()yt=e+e-eetêúë442ûé1-2t(jt-jt)3-2t(jt-jt)1-tù()=êee+e+jee-e-eúetë442ûé1-2t3-2t1-tù()=ecost+esint-eetêúë222û2t2t-2t4.12对一个LTI系统，已知：输入信号f(t)=4ee(-t)；输出响应y(t)=ee(-t)+ee(t)（1）确定系统的系统函数H(s)及收敛域；（2）求系统的单位冲激响应h(t)；-t（3）如果输入信号f(t)为f(t)=e,-¥0t®¥t®¥即收敛域为s<2。2t-2t输出响应y(t)=ee(-t)+ee(t)11其拉普拉斯变换为Y(s)=-+s-2s+22t-st-2t-stlimee+limee=02-s>0且2+s>0t®¥t®¥229 即收敛域为-20时的s域电路如图4.13所示。以I(s)、I(s)为变量对两个网孔列KVL方程为：12图4.13æ1ö()æ1ö()()ç1+1+÷I1s-ç1+÷I2s=U1sèsøèsøæ1ö()æ11ö()()-ç1+÷I1s+ç1++÷I2s=-kU2sèsøèssø246 又有1U(s)=[I(s)-I(s)]212sU(s)=kU(s)32整理以上四式，并联解得kU(s)=U(s)32()1s+3-ks+1即有U3(s)kH(s)==()2()Uss+3-ks+11（2）若H(s)的极点全部位于s平面的左半开平面，系统就是稳定的。欲使整个系统稳定，则必须有3-k>0，故得k<3（3）取k=2,u(t)=sinte(t)时，有12U(s)=U(s)321s+s+11U(s)=12s+11将U(s)=代入U(s)中，得到：123s+121U(s)=×322s+s+1s+1éùê13ús+ê212sú=2ê22+22-2úêæ1öæ3ö3æ1öæ3ös+1úêçs+÷+çç÷÷çs+÷+çç÷÷úëè2øè2øè2øè2øû故得1-téù313u(t)=22e2êúcost+-sintee(t)costt()3ëû223（4）取k=3,u(t)=coste(t)时，有13U(s)=U(s)321s+1sU(s)=12s+1s将U(s)=代入U(s)中，得到：123s+1247 3ss32Us3()=×22=×2ss++112(s2+1)故得3u(t)=tsinte(t)32（5）取k=3,u(t)=cos2te(t)时，有13U(s)=U(s)321s+1sU(s)=12s+4s将U(s)=代入U(s)中，得到：123s+43sssU(s)=×=-32222s+1s+4s+1s+4故得u(t)=(cost-cos2t)e(t)3248'