基于鸽子群优化算法的四旋翼无人直升机姿态控制.pdf 11页

'˖ڍመ੾᝶஠ڙጲhttp://www.paper.edu.cn基于鸽子群优化算法的四旋翼无人直升机姿态控制朱兵，陈谋南京航空航天大学自动化学院，南京　210016摘要：比例，积分，微分(PID)控制方法在如今的四旋翼无人直升机姿态控制中得到了广泛应用。然而，由于四旋翼无人机自身系统所带有的不确定性以及外部环境产生扰动的存在，一组固定不变的PID参数难以满足四旋翼无人直升机复杂环境下的各种飞行需求。并且，传统的PID姿态控制器参数需要手动调节，耗时费力且难以达到满意的控制效果。基于此，本文研究一种基于鸽子群的优化算法来寻找合适的PID参数。通过对是否含有基于鸽子群优化算法的PID控制器和神经网络PID控制器的比较，可以发现鸽子群优化算法具有全局快速搜索能力，且本文研究的控制器相较于传统的PID控制器具有更好的灵活性，自适应性，精确性以及鲁棒性。关键词：四旋翼无人直升机，鸽子群优化算法，姿态控制，PID控制中图分类号：V278AttitudeControlforQuadrotorsBasedonPigeon-InspiredOptimizationAlgorithmZHUBing,CHENMouCollegeofAutomationEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016Abstract:Proportional,integralanddifferential(PID)controlmethodiswidelyappliedinattitudecontrolforquadrotors.However,agroupofinvariablePIDparameterscannotmeetquadrotor’sflightcontrolrequirementsduetothequadrotor’ssystemuncertaintyandexternaldisturbance.And,thetraditionalPIDcontroller’sparametersofquadrotor’sattitudecontrolneedmanualoptimizationwhichistime-consumingandisdifficulttoachievethesatisfactorycontrolperformance.Inordertosolvethisproblem,thepigeon-inspiredoptimization(PIO)algorithmisusedinthispapertofindthesuitablePIDparameters.BycomparingthesimulationresultsthatPIOalgorithmcombinedwithPIDcontrollerandtheneuralnetworkPIDcontrollerrespectively,wecanfindthatPIOalgorithmhastheglobalsearchingabilityandfastsearchingability.Andthecontrollerdevelopedinthispaperhasabetterflexibility,adaptability,accuracyandrobustnessthanthatofthetraditionalPIDcontroller.基金项目：高等学校博士学科点专项科研基金(20133218110013)作者简介：朱兵（1991-），男，博士生，主要研究方向：飞行控制、非线性控制、预测控制,邮箱地址:zhub-ing91@163.com。通信作者：陈谋（1975-）,男，教授、博士生导师，主要研究方向：飞行控制、非线性控制、鲁棒控制等,邮箱地址:chenmou@nuaa.edu.cn。-1- ˖ڍመ੾᝶஠ڙጲhttp://www.paper.edu.cnKeywords:Quadrotors,PIOAlgorithm,AttitudeControl,PIDControl0引言最近，四旋翼无人直升机由于能够垂直起降，搭载其他设备以及飞行灵活等特点吸引了许多研究者的目光。基于此，四旋翼无人直升机广泛应用于安保监视，搜寻营救以及资源侦察探索[1]等各种不同领域。而这些任务的顺利完成，需要四旋翼无人直升机有一个高效的控制系统。然而，四旋翼无人直升机的控制模型是一个欠驱动，强耦合并且对外部扰动十分敏感的多输入多输出系统。由于四旋翼无人直升机具有六自由度及四个通道的控制输入，设计它的控制系统并不容易。到目前为止，存在着各种关于四旋翼无人直升机的线性以及非线性控制方法。在文[2]中，将PID控制方法和一些线性控制方法作了比较，并提出一种反馈控制方法。在文[3]中，也将反馈控制方法用于四旋翼无人直升机的控制当中，并取得了满意的控制效果。在文[4]中，作者将滑模控制方法应用于四旋翼无人直升机的控制。非线性反步控制方法也被研究过并被应用到该领域中[5]。在文[6]中，基于粒子群优化算法的神经网络PID控制方法也被提出并应用到四旋翼无人直升机的控制当中。但是，由于PID控制方法设计简单，灵活方便等特点，在四旋翼无人直升机的实际应用中，PID控制方法仍然是应用最广，最普遍的控制方法。传统PID控制结构可大致分为两个部分。一个为控制四旋翼无人直升机俯仰，滚转，偏航的姿态内环控制，另一个为控制四旋翼无人直升机上下，左右以及前后飞行的外环轨迹控制。内环姿态控制是外环轨迹控制的基础。内环姿态控制的效果直接影响到外环轨迹的控制。另一方面，PID控制参数并不是相互孤立的，它们间相互影响。其中的一个参数发生改变，另外的参数也需要同时做出调整。而实际的PID参数调整选取过程往往需要大量的实际经验做保证，耗时费力，且难以得到最满意的控制参数。此外，PID控制方法没有自适应能力，当四旋翼无人机的内部结构发生变化，或者受到外部扰动的影响时，就需要重新调整参数来获得最优控制效果[7]。神经网络能够根据性能指标J来调整PID控制器的参数值。然而，它的权值调整很容易陷入局部最优的状态中。最近，北京航空航天大学的段海滨教授提出了一种新型的鸽子群优化算法[8]。根据四旋翼无人直升机的PID控制器参数优化问题，本文研究一种将神经网络PID控制器和鸽子群优化算法相结合的新的控制方法。通过与传统PID控制方法的MATLAB仿真结果比较，发现基于鸽子群优化算法的神经网络PID控制器能够到达让人满意的效果。1四旋翼无人直升机模型四旋翼无人直升机的机体可视为一个对称刚体结构。如图一所示，相对的两个旋翼的旋转方向相同，而相邻的两个旋翼的旋转方向相反。因此，当四个旋翼的转速相同时，每个支架所受的回转力矩总和为零，从而有效地避免了四旋翼无人机的偏航转动[9]。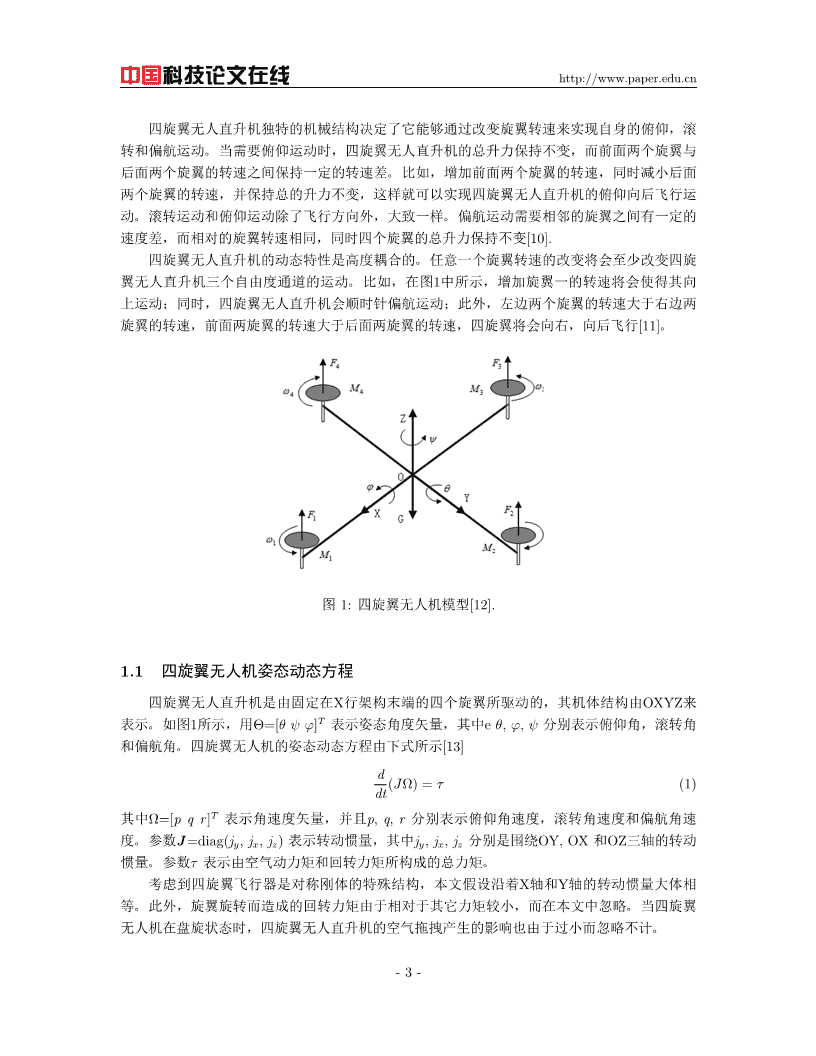-2- ˖ڍመ੾᝶஠ڙጲhttp://www.paper.edu.cn四旋翼无人直升机独特的机械结构决定了它能够通过改变旋翼转速来实现自身的俯仰，滚转和偏航运动。当需要俯仰运动时，四旋翼无人直升机的总升力保持不变，而前面两个旋翼与后面两个旋翼的转速之间保持一定的转速差。比如，增加前面两个旋翼的转速，同时减小后面两个旋翼的转速，并保持总的升力不变，这样就可以实现四旋翼无人直升机的俯仰向后飞行运动。滚转运动和俯仰运动除了飞行方向外，大致一样。偏航运动需要相邻的旋翼之间有一定的速度差，而相对的旋翼转速相同，同时四个旋翼的总升力保持不变[10].四旋翼无人直升机的动态特性是高度耦合的。任意一个旋翼转速的改变将会至少改变四旋翼无人直升机三个自由度通道的运动。比如，在图1中所示，增加旋翼一的转速将会使得其向上运动；同时，四旋翼无人直升机会顺时针偏航运动；此外，左边两个旋翼的转速大于右边两旋翼的转速，前面两旋翼的转速大于后面两旋翼的转速，四旋翼将会向右，向后飞行[11]。图1:四旋翼无人机模型[12].1.1四旋翼无人机姿态动态方程四旋翼无人直升机是由固定在X行架构末端的四个旋翼所驱动的，其机体结构由OXYZ来表示。如图1所示，用Θ=[θψφ]T表示姿态角度矢量，其中eθ,φ,ψ分别表示俯仰角，滚转角和偏航角。四旋翼无人机的姿态动态方程由下式所示[13]d(JΩ)=τ(1)dt其中Ω=[pqr]T表示角速度矢量，并且p,q,r分别表示俯仰角速度，滚转角速度和偏航角速度。参数J=diag(jy,jx,jz)表示转动惯量，其中jy,jx,jz分别是围绕OY,OX和OZ三轴的转动惯量。参数τ表示由空气动力矩和回转力矩所构成的总力矩。考虑到四旋翼飞行器是对称刚体的特殊结构，本文假设沿着X轴和Y轴的转动惯量大体相等。此外，旋翼旋转而造成的回转力矩由于相对于其它力矩较小，而在本文中忽略。当四旋翼无人机在盘旋状态时，四旋翼无人直升机的空气拖拽产生的影响也由于过小而忽略不计。-3- ˖ڍመ੾᝶஠ڙጲhttp://www.paper.edu.cn在这种情况下，空气动力矩可以分为俯仰力矩τθ，滚转力矩τφ和偏航力矩τψ，并且由公式所示[12]τθ=l(F1+F2F3F4)τφ=l(F1F2F3+F4)(2)τψ=M1M2+M3M4其中l是四旋翼无人直升机中心到旋翼旋转中心的距离，Fi(i=1,2,3,4)表示四个旋翼生成的总推力，Mi(i=1,2,3,4)表示第i个旋翼生成的力矩。力矩和推力公式可写成如下所示[12]{F=cw2ii(3)M=cw2iψi其中wi(i=1,2,3,4)表示第i个旋翼的转速,c表示旋翼上拉系数，cφ表示旋翼的反力矩系数。从公式(1)-(3)可以得出如下所示的四旋翼无人直升机姿态动态方程[12]θ˙=pcosφ+rsinφφ˙=q+psinφtanθ+rcosφtanθψ˙=psinφ/cosθ+rcosφ/cosθ(4)p˙=τθ/jyq˙=τφ/jxr˙=τψ/jz1.2四旋翼无人机旋翼解析为了使得四旋翼无人直升机能够跟踪期望的姿态，需要将控制输入从三个力矩到4个旋翼转速进行转换。四旋翼旋翼所需的转速公式由下式所示[12]w21111T1dclclclc0w21111u2d=1clclclc1(5)w241111u3dclclclc2w21111u4dclclclc3其中wid(i=1,2,3,4)表示第i个旋翼的转速，ui(i=1,2,3,4)是第i个通道的控制信号。T0表示四个旋翼生成的总推力。2控制器设计2.1鸽子群优化算法简介鸽子群优化算法由北京航空航天大学段海滨教授研究组提出，下面根据其发表的论文对鸽子群优化算法进行简单介绍。-4- ˖ڍመ੾᝶஠ڙጲhttp://www.paper.edu.cn鸽子群优化算法使用基于速度，位置的搜索模型，每个鸽子的位置相当于搜寻空间一组候选解向量，且能够以一定的速度移动。从鸽子群优化算法中可知，下一次迭代的飞行速度可由当前的速度和位置以及种群的最中心位置所决定的。而每个鸽子的下一代最优位置与当前的本身位置和速度相关。这些鸽子都能够在每次迭代过程中调整飞行方向从而最终达到目的地[14]。为了完全描述出鸽子群的寻找目的地的特点，通过如下一些规则设计两个操作算子；2.1.1罗盘算子鸽子群可以通过自身感应接收地球的磁场，从而在其脑中形成飞行路线图。它们根据太阳高度作为罗盘来调整飞行方向。而鸽子越飞抵目的地时，它们越是减少对该方法的依赖。在鸽子群优化算法模型当中，使用了一群类似的虚拟的鸽子。在罗盘算子中，定义了第i个鸽子的位置Xi和速度Vi，并且这些鸽子的速度和位置在每一次的迭代中都会更新。在每一次迭代中，新的速度和位置公式由如下公式所示[15]:{V(t+1)=V(t)+rand(pbestX(t))(6)X(t+1)=X(t)(1exp(Rt))+V(t+1)其中，R是罗盘算子的操作因子，rand是0和1之间的一个随机数，pbest是当前鸽子群的全局最佳位置，并且该位置可通过比较所有的鸽子位置来得到。在罗盘算子中，所有鸽子中的最优位置通过使用该算子获得。每个鸽子通过公式(6)来不断的调整它们的飞行方向。2.1.2地标算子在地标算子中，鸽子群的鸽子数量在每一次的迭代中都会减少一半。然而，这些鸽子仍然离目的地很远，并且它们对地标不熟悉。令Xc(t)作为每次迭代鸽子群的中心位置，并且假设每一个鸽子可以直接飞向目的地。鸽子的位置和速度更新公式由下公式给出[16]：N(t)=Np(t1)p2∑X(t)=X∑i(t)
fitnessXi(t))(7)cNpfitness(Xi(t))Xi(t)=Xi(t1)+rand
(Xi(t)Xi(t1))其中，tness表示每个鸽子个体距离最优位置的距离，并且Np是当前鸽子群的种群数量。2.2基于鸽子群算法的PID控制器传统的PID控制器由于设计简单，便于理解等优点在许多种应用中使用。然而，在设计PID参数时很麻烦，且参数一旦确定，控制器自身便不能够改变参数，因此，传统的PID控制器没有自适应性。所以对于系统结构变化和外部可能受到扰动时，该控制器不在最优状态。-5- ˖ڍመ੾᝶஠ڙጲhttp://www.paper.edu.cn因此，由于鸽子群算法具有良好的优化能力，本节研究基于鸽子群优化算法的PID控制器。关于该控制器的控制框图由图2所示。呭ᆀ㗔Ոॆ㇇⌅e(t)r(t)y(t)PID᧗ࡦಘഋ᯻㘬ᰐӪᵪ⁑රu(t)-图2:基于鸽子群优化算法的PID控制系统图.如图2所示，基于鸽子群优化算法的PID控制器由四旋翼无人直升机模型，PID控制器以及鸽子群优化算法三部分所构成。此外，r(t)是参考输入，y(t)是系统输出，e(t)是两者间的误差，u(t)是控制输入量。PID控制器通过鸽子群算法不断调整PID参数值。鸽子群优化算法寻找合适的PID参数可分为如下的一些步骤[17,18]：Step1:建立四旋翼无人直升机模型，并且初始化鸽子群优化算法的参数值，比如解空间维数D，总群数量，罗盘算子的操作因子，迭代次数以及最优性能指标。Step2：更新所有组的PID参数值，根据公式(6)来评估最优组的PID参数值和每组参数的适应度值可由如下性能指标J来得到。∫1J=t
je(t)jdt(8)0Step3：比较是否JNC1max，如果不是，跳到Step2；否则，到下一步。Step4:更新所有组的PID参数值，通过公式(7)来评估最优组视为PID参数值并且通过公式(8)来计算每组PID参数的适应度值。Step5:比较是否JNC2max，如果是，跳到Step2;否则，跳到Step4。Step6:令J=Jbest，然后保存最优PID参数值并且将这组值送给四旋翼无人直升机，然后跳到下一步。Step7:判断是否任务已经完成。如果没有，则跳到Step2；否则，结束当前任务。2.3基于鸽子群优化算法的神经网络PID控制器然而，基于鸽子群优化算法的PID控制器并非十分理想。由于神经网络具有趋近任何非线性关系的能力，结合鸽子群算法的自动搜索能力可以取得更好的效果，所以在本节研究一种基于鸽子群优化算法的神经网络PID控制器。下面是对它的一些简单介绍。本文的神经网络选取由输入层，隐含层和输出层的三层结构所组成的神经网络。并且输入层选取9个节点，对应于三个被控通道的累计误差，当前误差和误差的变化速度；输出层有9个-6- ˖ڍመ੾᝶஠ڙጲhttp://www.paper.edu.cn神经节点，代表四旋翼无人机三个被控通道的比例，积分和微分PID参数。中间层节点数不固定，本文选取个数为10个节点。基于鸽子群优化算法的神经网络PID控制系统框图如图3所示，流程图如图4所示。呭ᆀ㗔Ոॆ㇇⌅⾎㓿㖁㔌e(t)r(t)u(t)y(t)PID᧗ࡦಘഋ᯻㘬ᰐӪᵪ⁑ර-图3:基于鸽子群优化算法的神经网络PID控制系统.ᔰ࿻ࡍ࿻ॆ⾎㓿㖁㔌઼呭ᆀ㗔㇇⌅ѝⲴ৲ᮠṩᦞ㖇ⴈ㇇ᆀޜᔿ(6)ᴤᯠ⇿㓴⾎㓿㖁㔌ᵳ٬઼PID৲ᮠˈ䇑㇇ࠪᖃࡽᴰ㓴৲ᮠ٬઼ᙗ㜭ᤷḷ৲ᮠJYᱟ੖JC1max˛Yṩᦞൠḷ㇇ᆀޜᔿ(7)ᴤᯠ⇿㓴⾎㓿㖁㔌ᵳ٬઼PID৲ᮠˈ䇑㇇ࠪᖃࡽᴰ㓴৲ᮠ٬઼ᙗ㜭ᤷḷ৲ᮠJYᱟ੖JC1max˛YԔJ=J_best,؍ᆈᖃࡽPID৲ᮠ٬ˈᒦሶᆳԜ䍻٬㔉PID᧗ࡦಘNᱟ੖Nc>C2Max˛Y㔃ᶏ图4:基于鸽子群优化算法的神经网络PIID控制器算法流程图.基于鸽子群优化算法的神经网络PID控制器的四旋翼无人直升机姿态控制可分为如下几个步骤[17,18]：Step1:建立四旋翼无人机数学模型，初始化鸽子群优化算法和神经网络的初始值，比如-7- ˖ڍመ੾᝶஠ڙጲhttp://www.paper.edu.cn解空间维数D，种群数量Np，罗盘算子操作因子，两种算子迭代次数NC1max和NC2max和最优性能指标Jbest的初始值。Step2:更新所有组神经网络的权值，并且用公式(6)评估最佳组的神经网络权值，然后计算出相应的PID参数值，再用公式(8)计算与之相对应的适应度值。Step3:判断是否JNC1max，如果不是，跳到Step2；否则，跳到下一步。Step4:更新所有组鸽子群的神经网络权值，然后通过公式(7)评估最优组的神经网络权值，并且计算出相对应的PID值和适应度值。Step5：判断是否JNC2max，如果是的话，跳转到Step2；否则，跳转到Step4。Step6：令J=Jbest，然后保存优化后的PID参数值并且将它们发送给四旋翼无人直升机，然后跳往下一步。Step7:判断任务是否完成。如果没有完成，跳到Step2；否则的话，结束任务。3仿真结果本节通过对上述算法的仿真实验，可以得到优化后的PID参数值和对应的适应度值。并且比较鸽子群算法结合PID控制器和神经网络PID控制器的仿真结果，更能够进一步体现鸽子群优化算法的特点。四旋翼无人直升机的模型参数如下表1所示。表1:四旋翼无人机模型参数重力(G)12N杆距(l)0.275m升力系数(c)1.335107N
min/r反力矩系数(c)1.5108N
min/rφX轴转动惯量(J)6.23103Nm
s2/radxY轴转动惯量(J)6.23103Nm
s2/radyZ轴转动惯量(J)1.12102Nm
s2/radz四旋翼无人直升机的鸽子群优化算法结合PID控制器的阶跃响应曲线如图5所示，其适应度曲线图如图6所示。四旋翼无人直升机基于鸽子群优化算法的神经网络PID控制器的阶跃响-8- ˖ڍመ੾᝶஠ڙጲhttp://www.paper.edu.cn应曲线由图7所示，且其适应度曲线如图8所示。6625realrealrealcommandcommandcommand5520441533Pitch(deg)Roll(deg)Yaw(deg)1022511000012345012345012345Time(sec)Time(sec)Time(sec)(a)俯仰通道阶跃响应(b)滚转通道阶跃响应(c)偏航通道阶跃响应图5:四旋翼基于鸽子群优化算法的PID控制器的俯仰，滚转，偏航三通道的阶跃响应曲线30Thecarveoffitness252015Thefitnessvalue105020406080100120Thenumberofiterations图6:基于鸽子群优化算法的PID控制器的权值适应度曲线.从上面的仿真结果可以发现，基于鸽子群优化算法的PID控制器适合四旋翼无人直升机的有效控制；并且，基于鸽子群优化算法的神经网络PID控制器有更好的控制性能。6725realrealrealcommandcommandcommand6520541543Pitch(deg)Roll(deg)3Yaw(deg)1022511000012345012345012345Time(sec)Time(sec)Time(sec)(a)俯仰通道阶跃响应(b)滚转通道阶跃响应(c)偏航通道阶跃响应图7:四旋翼基于鸽子群算法的神经网络PID控制器的俯仰，滚转，偏航通道的阶跃响应曲线-9- ˖ڍመ੾᝶஠ڙጲhttp://www.paper.edu.cn80Thecarveoffitness70605040Thefitnessvalue302010020406080100120Thenumberofiterations图8:基于鸽子群优化算法的神经网络PID控制器的权值适应度曲线.4总结本文给出了一种优化四旋翼无人直升机PID控制参数的优化方法。仿真结果显示鸽子群算法是一种有效的参数优化方法。通过比较，可以发现PIO算法可以优化四旋翼无人机的PID权值，并且基于此算法的神经网络控制器的有更好的全局快速搜索能力。参考文献（References）[1]TayebiA,McGilvrayS.AttitudestabilizationofaVTOLquadrotoraircraft[J],IEEETrans-actionsonControlSystemsTechnology,2006,14(3):562-571.[2]KhatoonS,GuptaD,DasLK.PID&LQRcontrolforaquadrotor:Modelingandsimu-lation[C],AdvancesinComputing,CommunicationsandInformatics,2014:796-802.[3]TayebiA,McGilvrayS.Attitudestabilizationofafour-rotoraerialrobot[C],43rdIEEEConferenceonDecisionandControl,2004:1216-1221.[4]Luque-VegaL,Castillo-ToledoB,LoukianovAG.Robustblocksecondorderslidingmodecontrolforaquadrotor[J],JournaloftheFranklinInstitute-EngineeringandAppliedMath-ematics,2012,349(2):719-739.[5]LeeD,KimHJ,SastryS.Feedbacklinearizationvs.adaptiveslidingmodecontrolforaquadrotorhelicopter[J],InternationalJournalofControlAutomationandSystems,2009,7(3):419-428.[6]DierksT,JagannathanS,Outputfeedbackcontrolofaquadrotoruavusingneuralnet-works[J],IEEETransactionsonNeuralNetworks,2010,21(1):50-66.-10- ˖ڍመ੾᝶஠ڙጲhttp://www.paper.edu.cn[7]GuenardN,HamelT,MahonyR.Apracticalvisualservocontrolforanunmannedaerialvehicle[J],IEEETransactionsonRobotics,2008,24(2):331-340.[8]DuanHB,LuoQ.Newprogressesinswarmintelligence-basedcomputation[J],InternationalJournalofBio-InspiredComputation,2015,7(1):26-35.[9]GanD,CaiG,DiasJ,SeneviratneL.Attitudecontrolofquad-rotorUAVsusinganintuitivekinematicsmodel[C],2013IEEE20thInternationalConferenceonElectronics,Circuits,andSystems(ICECS),2013:597-600.[10]McKerrowP.ModellingtheDraganflyerfour-rotorhelicopter[C],Proceedingsofthe2004IEEEInternationalConferenceonRobotics&Automation,2004:3596-3601.[11]GaitanA,BoleaY.Modelingandrobustattitudecontrolofaquadrotorsystem[C],Pro-ceedingsof10thInternationalConferenceonElectricalEngineering,ComputingScienceandAutomaticControl,2013:7-12.[12]WeiQT,WangHL,WuQX,ChenM.Backstepping-basedattitudecontrolforaquadrotorUAVwithnonlineardisturbanceobserver[C],201534thChineseControlConference(CCC),2015:771-776.[13]Bouabdallah,Samir.Siegwart.Fullcontrolofaquadrotor[C],2007IEEE/RSJinternationalconferenceonintelligentrobotsandsystems,2007:153-158.[14]DuanHB,LiuSQ.Nonlineardual-moderecedinghorizoncontrolformultipleUAVsformationflightbasedonchaoticparticleswarmoptimization[J],IETControlTheory&Applications,2010,4(11):2565–2578.[15]SunH,DuanHB.PIDcontrollerdesignbasedonprey-predatorpigeon-inspiredoptimiza-tionalgorithm[C],Proceedingsof2014IEEEInternationalConferenceonMechatronicsandAutomation,2014:1416-1421.[16]LiH,DuanHB.Blochquantum-behavedpigeon-inspiredoptimizationforcontinuousoptimizationproblems[C],Proceedingsof2014IEEEChineseGuidance,NavigationandControlConference,2014:2634-2638.[17]DuanHB,WangXH.Echostatenetworkswithorthogonalpigeon-inspiredoptimizationforimagerestoration[J],IEEEtransactionsonneuralnetworksandlearningsystems,2016,27(11):2413-2425.[18]HuYW,DuanHB.Gaussianentropyweightpigeon-inspiredoptimizationforrectangularwaveguidedesign[C],IEEEchineseguidance,navigationandcontrolconference(CGNCC),2016:1951-1956.-11-'